构造变形的物理机制可以为地震机理与地震预测的研究提供理论基础.构造变形主要包括两大类:脆性变形和塑性变形.脆性变形的重要方面之一就是断层的摩擦滑动.由于历史上大部分地震都是沿着已有断层的重复活动[1],且很多大地震都是在断层闭锁段发生的,即断层局部克服了摩擦力而发生的突然错动.断层摩擦方面的研究在脆性变形中处于非常重要的位置.断层在摩擦滑动过程中势必产生断层泥[2],断层泥作为一种较“软”的物质夹于围岩之间,其摩擦性质控制着断层整体的摩擦性质,断层泥的剪切强度就是断层的强度,这一点在岩石力学实验研究中已形成共识[1].而且含断层泥的断层是可以闭锁-错动-再闭锁,形成周期,表现在实际地震过程中就是一个称为“地震破裂”的错动.虽然破裂和摩擦都是地壳脆性变形的主要方式,但地壳岩石是发生破裂还是摩擦,取决于两者的强度大小,如果完整岩石的破裂强度大于已经存在的断层的摩擦强度,断层优先发生摩擦滑动.而地壳中已经存在大量的断层,摩擦滑动成为地壳脆性变形的主要变形方式.断层摩擦强度取决于摩擦系数和正应力,由于大部分断层的摩擦系数在0.65~0.73,而且存在断层泥与否,并不会降低摩擦系数(摩擦系数的大小主要受控于矿物组分).断层摩擦强度随着深度会增加,并且与岩石的破裂强度接近[3].
在断层泥的摩擦滑动实验研究中有2个需要关注的重要问题:第一是摩擦系数的大小问题;第二是摩擦滑动的方式问题,即摩擦滑动的稳定性问题.在特定的构造环境条件下将摩擦强度与岩石本身的流变强度进行对比可以粗略判别岩石的变形机制,因此摩擦强度对于推测和确定地壳的流变结构具有重要意义;而滑动的稳定与否则直接关系到是否在断层上产生地震.断层摩擦过程中出现的黏滑(速率弱化的一种表现形式),是强震发生的主要物理机制.
地震波速结构探测表明,地壳中的物质存在分层结构[4],大部分结晶基底地层大体可分成三层:上层以花岗质岩石为主;下层主要是铁镁质岩石,成分大致与辉长岩相当;而中间过渡层则以中性岩石为主,成分大致如闪长岩.由于中性岩处于中地壳这样重要的位置,我们需要对其力学性质给以应有的关注.为此,在本研究中我们特别关注中地壳的代表性岩石闪长岩.斜长石和角闪石是闪长岩的主要组成矿物,了解这两种矿物的摩擦滑动性质有助于对闪长岩性质在更深层次上的把握.同样重要的是,角闪石作为一种含水矿物,其摩擦滑动性质与名义无水矿物如石英、长石是否存在差别,是否有特殊之处,也是我们感兴趣的重要问题.基于此,本文着重讨论角闪石的摩擦滑动性质,并与罗丽等关于斜长石[5]的摩擦滑动性质进行对比.
作为描述岩石摩擦滑动行为的理论框架,基于实验研究的速率与状态摩擦本构关系目前已被广泛接受[6, 7].这种本构关系可以很好地描述岩石摩擦滑动的力学行为,抓住了摩擦滑动中力学现象的主要宏观规律.在有效正应力σ恒定条件下,当滑动速率从V*变化到V时,摩擦系数对此会产生瞬时响应,即aln(V/V*),其中a是表征直接速率效应的本构参数.之后摩擦剪应力τ会进入一个衰减过程,向新的稳态值过渡.这个过程中剪应力的变化用一个状态变量θ的函数来描述,即bln(θ/θ*),其中θ*表示某一参照速率V*下对应的稳态值,b是表征这种过渡过程强弱的本构参数.由此,广义上的摩擦系数μ=σ/τ可描述为[8]
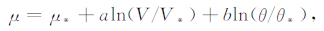
|
(1) |
这里μ*表示在参照速率V*下的摩擦系数稳态值.
过渡过程中θ值是随着滑动位移或时间演化的,因此在速率切换的瞬间将保持其原有的状态值.目前有两种最常用的演化方程.一种是滑动本构关系,即状态变量只随着滑动距离而演化,如(2)式所示.
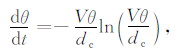
|
(2) |
其中dc是摩擦系数演化的特征滑动距离.
另一种则可以描述静止接触时间的效应,称为慢度本构关系[9],如(3)式所示.
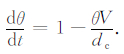
|
(3) |
在考虑准静态实验中摩擦对速度变化响应的情况时,大部分数据都可以与这两种本构关系很好地拟合.由于在静接触时间效应的有无上有实质性差别,因此在一些非常缓慢的实验过程如滑动-位移保持-滑动实验中,两种本构关系差别较大,而实验结果更接近慢度本构关系[9],同时在对接触面的直接观察中发现接触面积确实随静接触时间增加而增加[10].
在任意速率V下,dθ/dt=0时即为该速率下的稳态,此时的状态变量值为θss=dc/V,其中下标ss表示稳态值.代入(1)式就可得到摩擦系数的稳态值:
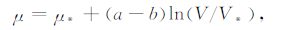
|
(4) |
(4)式在速率从V1向V2变化后的差分形式如下:
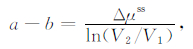
|
(5) |
其中a-b是描述摩擦滑动稳定性的重要参数,称为速率依赖性参数.a-b为正时,稳态摩擦系数随着速率的增加而增加,称为速率强化,反之为速率弱化.
摩擦滑动稳定性的基本规律可以通过分析单自由度弹簧-滑块系统来获得.在小扰动情况下,将本构关系线性展开后进行线性稳定性分析,可以得到准静态情况下系统的稳定性条件[7].在小扰动条件下,当系统的刚度k小于某一临界值kcr(称其为临界刚度)时,系统不稳定,而大于这一临界值的情况则是稳定的.当系统刚度与临界刚度相等时,系统则以周期性振荡的形式运动.临界刚度kcr与摩擦本构关系中的稳态速率依赖性参数a-b、特征滑动距离dc、有效正应力σ有如下关系[7]:
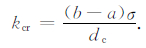
|
(6) |
分析公式(6)可知:在速率强化条件下(a-b > 0),kcr < 0,不可能出现系统刚度小于临界刚度的情况,所以在小扰动条件下不管刚度如何都是稳定的;在速率弱化情况下(a-b < 0),此时kcr是有限值,b-a值越大临界刚度也越大,微小扰动就很有可能产生不稳定滑动.而对于连续介质中的断层来说,在稳定的构造加载作用下,只有当a-b < 0时,不稳定滑动成核才能出现[11, 12];相反,较大的dc值则与较小的临界刚度相对应,有利于达到稳定滑动的条件.而有效正应力的增大,则对应临界刚度的增大,有利于不稳定滑动的出现.
由于速率弱化与断层上发生不稳定滑动成核直接相关,a-b值是摩擦滑动实验中最为关注的参数,它受断层面性状(粗糙程度等)、断层泥矿物成分、温度、正应力以及孔隙流体诸多因素的影响,且其影响不是相互独立的.在其他条件不变的情况下,温度变化无疑是最重要的影响因素.
基于以上研究背景,一些高温高压实验给出了地壳中代表性岩石的摩擦滑动性质,如花岗岩、辉长岩.Lockner等[13]考虑了温度对于花岗岩摩擦系数速率依赖性的影响,结果发现几乎与温度的变化无关,但没有考虑孔隙流体对速率依赖性的影响;Blanpied等[14, 15]不仅考虑了温度的因素,同时考虑了孔隙水压的因素,发现花岗岩的速率依赖性随着温度升高产生了从速率弱化向速率强化的转变;对于花岗岩的主要组成矿物石英,Chester等[16]给出了干、湿两种情况下其速率依赖性随着温度的变化.发现这两种情况的速率依赖性特征是不同的.但对于湿的同样也发现随着温度升高而产生的这种转变.表明石英作为花岗岩的主要组成矿物起到了控制性的作用.何昌荣等[17, 18]研究了干、湿不同情况下辉长岩摩擦滑动随温度的变化情况,发现加孔隙压力之后的速率依赖性随温度增加从速率弱化向速率强化转化,而在干燥情况下,在615℃的高温下仍然出现了由于速率弱化产生的黏滑现象.显然干、湿不同情况有着重要的差别.对于辉长岩的主要矿物斜长石和辉石,谭文彬等[19]和罗丽等[5]分别研究了干和湿两种情况下的摩擦滑动性质,同样表明了孔隙压力的存在具有重要影响.罗丽等[5]发现虽然斜长石和辉石是辉长岩的主要组成矿物,但并没有完全控制辉长岩摩擦系数的速率依赖性,而是作为次要矿物的石英[20]对辉长岩的摩擦滑动性质起到了控制性的作用.显然,不同岩石的摩擦力学性质可能存在巨大的差别,而其各自的摩擦滑动的微观机制也不可能符合相近的模式.总之,前人的结论告诉我们,温度和孔隙水的存在对于摩擦滑动是非常重要的,温度升高有利于滑动的模式向稳定滑动(速率强化)转变.此外,组成矿物对于岩石的摩擦滑动性质来说当然也是重要的影响因素.
本文着重考察温度和孔隙水压对矿物摩擦滑动的影响.实验温度范围为100~614 ℃,覆盖了大部分大陆地壳的温度范围;孔隙压力为30 MPa,以在较高温度条件下( > 317.5 ℃)实现超临界水的条件;有效正应力为200MPa.研究中将注意力同时放在温度对摩擦系数及其速率依赖性的影响.
2 实验方法及数据处理 2.1 实验方法本文中所有的摩擦实验都是在气体介质高温高压三轴实验系统[17]上进行的.利用氩气作为气体介质施加围压,可保证其压力均匀且可安全加温.温度采用YAMATAKE DCP30型控温仪,通过可控硅调节加温炉的功率来控制,设计最高温度为700℃.温度的施加形式为:T(目标温度)=5t(min)+T0(初始温度设定值).轴向加载由数字液压伺服机控制,设计轴压为100t;实验采用正应力恒定控制,并通过增减围压对轴压变化进行补偿来实现,在缓变条件下其控制误差为±0.5 MPa.这种控制在实验系统新增了一台增压器之后,用两个增压器配合加压,最后用其中一台进行控制,效果良好.此外,新增的高压腔真空系统也有利于对加温炉的氧化保护.
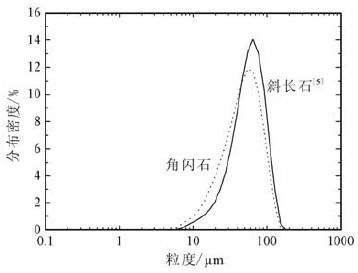
角闪石样品是从一种采自山东招平断裂带附近的斜长角闪岩中通过分离得到的.角闪石样品和岩粉在实验前于烘箱中在150 ℃条件下烘烤48h,然后放于干燥瓶中保存.岩粉通过手工粉碎后用200目筛进行粒度控制,粒度分布如图 1,其粒度中值是53μm.斜长石[5]的粒度中值是63μm.另外,为了初步考察角闪石和斜长石在闪长岩中的作用,选用采自龙门山断裂带附近彭灌杂岩中的一种闪长岩(其中斜长石和角闪石的含量分别为79.2%和20.6%)进行了少量的实验.同样粉碎过程后闪长岩的粒度中值为25μm.
围岩样品选用辉长岩,人工制成直径20 mm,长40mm圆柱状,过高的中心点沿与轴向夹角为35°的斜面将圆柱切成两部分,这两部分之间夹1mm厚的断层泥,结构类似于三明治.
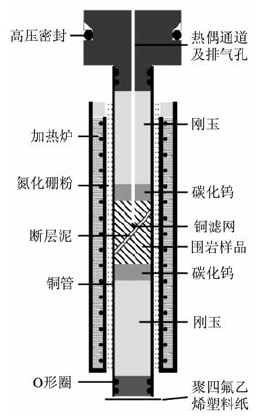
整个样品、碳化钨块以及刚玉柱全部封装在退火的铜管中(图 2),铜管壁厚0.35mm.铜管两头要用O型圈密封,以隔离围压介质和样品及孔隙水.围岩样品上下两部分,上半部分中心要钻直径2.5mm的小孔,在接近断层面时转折且与断层面呈90°,长5mm;将铜网卷塞入转折部分以防止断层泥挤入同时保证对孔隙水的高渗透性.铜管与加温炉之间要充填氮化硼粉末,用于传热并阻止气体对流.
|
图 2 气体围压三轴试验系统装样示意图 Fig. 2 Sketch of the sample assembly |
温度采用上下两段炉体分别加温,通过设定加温功率比例保证整个炉体内温度上下大致对称;650 ℃以下温度范围内样品中部与两端的温差控制在 < 14 ℃的范围内,且温度越低偏差越小.实验过程中实际温度值与设定值差值在2 ℃范围内.
轴向变形采用液压伺服系统,实验中的轴压通过设定变形速率来加载.本实验过程中采用1μm/s和0.1μm/s之间切换,以获取摩擦系数的速率依赖性数据.
2.2 数据处理实验过程中记录到的数据---轴向应力与轴向滑动位移关系曲线,它包含了系统刚度、传感器、铜管等诸多因素的影响,因此要进行各种因素的校正,最终得到真实的关系曲线.
第一步 压机弹性变形校正
轴向形变包含了压机的弹性形变(含样品以外所有垫块的变形),其刚度为473.5 MPa/mm,校正公式为

|
第二步 面积校正
三轴实验中测得的轴向应力是用单位面积的轴向压力表示.当上下滑块开始错动时,2个块体的实际接触面积开始减小,因此观测到的轴压(σ10)小于实际轴压(σ1c),它与轴向滑移量有如下关系[21]:
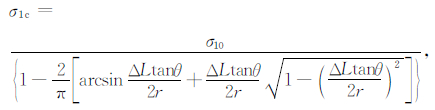
|
式中θ是轴线与断层面的夹角,本实验系统中为35°;r是围岩半径;ΔL是轴向滑移量,用测量得到的轴向位移与弹性应变的差值表示.若弹性应变向非弹性应变的转变点(即滑动起始点)为(Ds,σs),而弹性形变的斜率为K,则轴向滑移量如下:
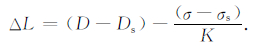
|
第三步 铜管强度校正
先计算剪切应力,剪应力计算公式如下:
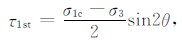
|
计算出来的值减去铜管的剪切强度,这是因为样品在剪切错动时,铜管也发生剪切变形,并产生一定阻力.将剪切强度减去对应错动位移下铜管的剪切强度就得到了断层泥样品的摩擦强度[22],即
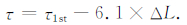
|
第四步1 有效应力校正
根据校正后的剪应力进而计算出相应的轴向应力和摩擦面上的正应力,即
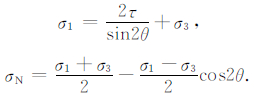
|
(6) |
正应力的计算值中要减去孔隙压力30MPa,得到的就是有效正应力σeff.
第五步 计算摩擦系数μ值
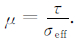
|
(7) |
第六步 计算速率依赖性a-b
稳滑时应用公式(5),即可得到a-b.由于变形曲线有微小的位移强化特性,具有一定的斜率,因此在取稳态值的差分值时需要用平行的斜线之间的距离来读取.
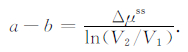
|
在变形曲线产生持续振荡时,由于不能获取稳态值,因此采用单状态变量本构关系的临界刚度来估算a-b的下限值,公式如下:

|
其中k=k1sin2 φcosφ,φ=55°,k1是压机和样品系统的总体刚度,可从加载曲线上读取;本实验的恒定有效正应力σeff为200 MPa;dc从稳滑曲线上读取.
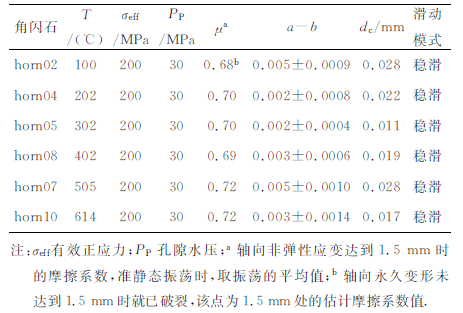
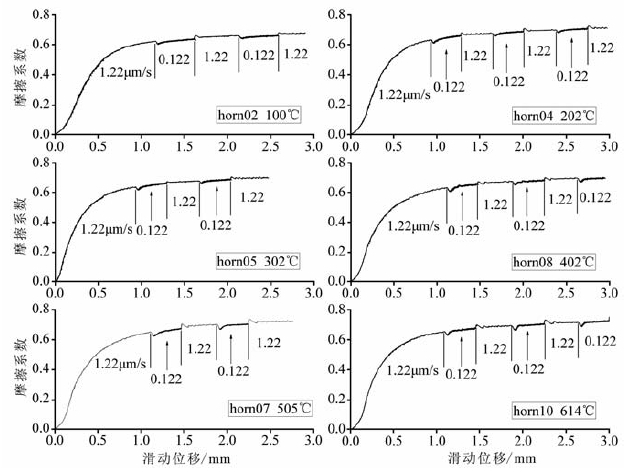
3 实验结果 3.1 力学数据实验中,先将初始围压设为152MPa,孔隙压力30 MPa,在轴压加载过程中当正应力达到230 MPa时,转为正应力控制,由此得到的有效正应力为200 MPa;实验的温度范围100~614 ℃.实验所得的角闪石断层泥摩擦系数-位移曲线如图 3所示.在此控制条件下获得的曲线特点表现为:在100~614 ℃范围内,均为速率强化,稳定滑动;曲线在稳定的剪切变形阶段表现非常平缓;瞬间响应系数a值在100~402℃范围内没有明显变化,但在505℃和614℃实验中显然较其他实验中的大.实验条件、摩擦系数、速率依赖性值以及特征滑动距离详见表 1.
|
图 3 角闪石在正应力230 MPa实验条件下的摩擦系数-滑动方向位移曲线 Fig. 3 Friction coefficient of hornblende gouge plotted as functions of displacement for a normal stress of 230 MPa |
|
|
表 1 热水条件下角闪石的实验条件与结果 Table 1 The experiment conditions and results of hornblende under hydrothermal conditions |
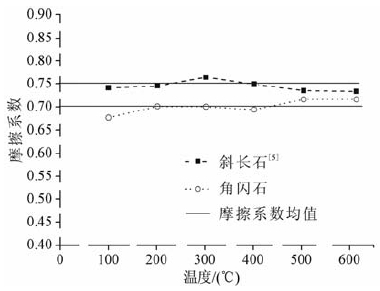
为了对比不同温度下的摩擦系数,我们选取了轴向非弹性变形为1.5mm(相当于滑动面上1.83mm)处,相同速率下的摩擦系数值(准静态振荡时,取振荡的平均值).图 4表明,角闪石的摩擦系数在0.70±0.01附近上下浮动,随着温度增加没有明显的规律性变化,呈离散分布.但在500 ℃和600 ℃时,摩擦系数趋于不变化.
|
图 4 角闪石、斜长石[5]的摩擦系数随温度的变化 角闪石和斜长石各点的摩擦系数为轴向永久变形达1.5mm时的值(相当于1.83mm的滑动量);在准静态振荡的情况下,取振荡的平均值,而且没有对速率效应作修正. Fig. 4 Friction coefficient of hornblende and plagioclase[5] gouges plotted against temperature The values of friction coefficient of hornblende gouge and plagioclase gouge picked at 1.5mm permanent axial displacement (equal to 1.83mm sliding distance under loading rate of 1.22μm/s).Average of oscillation amplitude was picked for cases of quasi-static oscillations. |
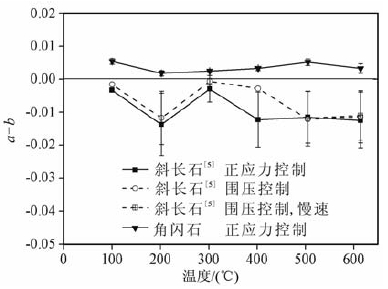
角闪石的摩擦滑动速率依赖性参数a-b(图 5)表明,在热水条件下,角闪石的速率依赖性在整个实验温度范围均表现为速率强化(a-b > 0),而且在202~505 ℃温度范围其速率依赖性有逐步增强的趋势.整个变化过程中,在202℃时的速率依赖性值最小.
|
图 5 角闪石和斜长石[5]的摩擦滑动速率 依赖性参数a-b与温度的变化关系慢速:滑动切换速率0.244μm/s和0.0488μm/s;围压为130 MPa恒定控制与正应力230 MPa恒定控制相当. Fig. 5 Rate dependence parameter a-b of horn blende and plagioclase[5] gouges plotted against temperature Slow velocity is 0. 244μm/s and 0. 0488μm/s. Confining pressure control (130 MPa) is the same as normal stress control (230 MPa) |
斜长石和角闪石作为闪长岩的主要组成矿物,无疑二者对闪长岩的摩擦滑动性质起着非常重要的作用.探明二者的摩擦滑动性质以及相互对比是本文的研究重点.
4.1 角闪石与斜长石的摩擦系数对比在已发表的斜长石[5]数据中,温度为101 ℃与298 ℃时,摩擦系数-滑动位移曲线表现为稳定滑动,同时显示微弱的速率弱化;201 ℃时出现振幅较小的持续性准静态振荡;397 ℃时,低速段曲线为稳滑,高速段出现准静态振荡;在501℃和606℃的高温段,斜长石表现为振幅较大的持续性准静态振荡.罗丽等[5]为验证实验的重复性以及在低速(滑动切换速率0.244μm/s和0.0488μm/s)下一致性,对斜长石断层泥还进行了与正应力230 MPa相当的,围压为130 MPa恒定控制的标速切换及高温段低速切换的实验.发现围压控制的实验结果与正应力控制的结果基本一致.
斜长石[5]的摩擦系数在低温段随着温度呈增加趋势(图 4),在300 ℃附近达到最大值;高温段则相反.整体上其摩擦系数值为0.75±0.01,均高于角闪石的摩擦系数(0.70±0.01).二者在500 ℃和600 ℃时,摩擦系数值趋于不变.
4.2 角闪石与斜长石的速率依赖性对比角闪石在整个实验温度范围内表现为速率强化(图 5),而斜长石[5]则相反,即均为速率弱化.角闪石和斜长石的粒度分布表明(图 1),在相同的磨碎过程之后,角闪石的粒度略小于斜长石的粒度,说明角闪石较斜长石易于碎裂,这可能由于角闪石的解理发育,从而易形成很小的颗粒.角闪石的这种易于破碎的性质可能使其易于以碎裂流动[23](颗粒不断重复破碎、滚动、相对摩擦滑动)的机制产生剪切变形,而且在宏观性质上体现为速率强化.
4.3 角闪石和斜长石对闪长岩的摩擦滑动性质的影响 4.3.1 摩擦系数谭文彬等[19]提出了辉石、斜长石以及辉长岩之间的摩擦系数满足一种简单的体积分数的加权平均关系,即用作为辉长岩的两种主要矿物斜长石和辉石在辉长岩中的体积分数进行摩擦系数的加权平均,计算得到的摩擦系数与辉长岩的摩擦系数相当.并认为辉长岩断层泥对外力的支撑基本上属于一种由主要矿物组成的并列支撑结构.那么闪长岩与其主要矿物之间是否也满足这种关系呢?
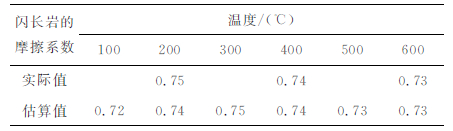
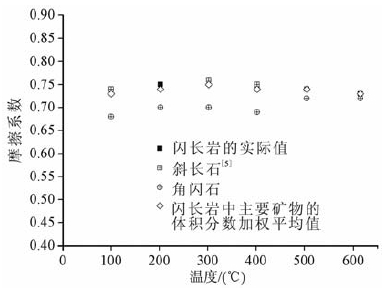
其中μ1和μ2分别是斜长石和角闪石断层泥的摩擦系数,而之前的系数为相应的体积分数.我们对闪长岩断层泥在200 ℃、400 ℃和600 ℃的温度条件下进行了补充实验,发现实验数据与估算值基本相符(表 2,图 6).这初步说明,闪长岩的摩擦系数与其主要组成矿物的摩擦系数之间也符合这种加权平均关系.进一步的确认有待在后续的实验中验证.
|
|
表 2 闪长岩摩擦系数的实际值和主要组成矿物的体积分数加权合成值 Table 2 Friction coefficient of diorite gouge and volume-weighted averages of the friction coefficients of plagioclase gouge and hornblende gouge |
|
图 6 闪长岩摩擦系数的体积分数加权合成值与实际摩擦系数的对比 Fig. 6 Friction coefficient of diorite gouge compared with volume-weighted averages of the friction coefficients of plagioclase gouge and hornblende gouge |
角闪石的存在使得闪长岩有向速率强化转变的趋势,而斜长石则正好相反.以往的实验结果表明[5, 19],岩石的速率依赖性参数不是其主要矿物速率依赖性参数值的平均值,由此推测闪长岩的速率依赖性也不一定是两种主要矿物的简单平均.我们研究的采自龙门山断裂带附近的闪长岩样品中角闪石的含量与斜长石的含量比例大概是1:3的关系.如前所述,角闪石较斜长石易于碎裂并形成很小的颗粒.使其易于以碎裂流动[23]的机制产生剪切变形,并在宏观性质上体现为速率强化.角闪石在闪长岩中的含量以及其本身的性质说明角闪石小颗粒可以充填于斜长石颗粒之间的空隙中,因此在剪切变形过程中,就有可能会发生类似于碎裂流动的变形机制,在这种情况下,力学性质上有利于速率强化的出现,这种可能的机制需要闪长岩的摩擦实验数据进一步加以验证.
5 结论本文基于速率与状态依赖性摩擦本构关系框架,为了解闪长岩中角闪石的摩擦系数及其滑动速率依赖性随温度的变化,进行了热水条件下的摩擦滑动实验研究,同时结合罗丽等[5]给出的斜长石的摩擦实验数据,对比了角闪石和斜长石[5]作为闪长岩的主要组成矿物的摩擦滑动性质.得出如下结论:
(1)在1.22μm/s的滑动速率下,轴向非弹性变形为1.5mm(相当于滑动面上1.83mm)处角闪石的摩擦系数值(准静态振荡时,取振荡的平均值)为0.70±0.01,明显低于斜长石[5]的摩擦系数值(0.75±0.01);角闪石的摩擦系数在整个温度范围内没有出现与温度相关的系统性变化,而斜长石[5]的摩擦系数随温度的变化呈“凸”起状,在300 ℃附近达到最大值.对闪长岩的补充实验表明,角闪石和斜长石的摩擦系数的体积分数加权平均值基本上反映了闪长岩的摩擦系数.这一结论需要系统的实验来验证.
(2)在热水条件下,角闪石在实验温度范围内均表现为速率强化,而斜长石[5]在100~605 ℃范围内则均表现为速率弱化;角闪石的速率强化特性在 > 200 ℃的温度范围有逐步增强的趋势,而斜长石[5]的速率依赖性则基本上表现为很强的速率弱化特性.
本研究存在的问题是,在更低的速率条件下摩擦滑动是否具有同样的性质需要进一步的实验来确认.这一点对于实验结果在构造变形环境中的应用非常重要.
为了全面地了解闪长岩的摩擦滑动性质以及组成矿物和岩石之间的关系,我们在后续的工作中将系统地研究闪长岩的摩擦滑动,同时兼顾更低滑动速率的情况.
致谢在论文的撰写过程中,周永胜研究员给予了建设性意见;在实验样品加工过程中,党嘉祥提供了技术支持;在实验数据处理方面,得到了罗丽极大的帮助和指导.在此一并表示感谢.
| [1] | Scholz C H. The Mechanics of Earthquakes and Faulting. Cambridge University Press, 2002. 265~273 |
| [2] | Engelder J T. Cataclasis and the generation of fault gouge. Bull. Geol. Soc. Am. , 1974, 85: 1515-1522. DOI:10.1130/0016-7606(1974)85<1515:CATGOF>2.0.CO;2 |
| [3] | Byerlee B J. Friction of rocks. Birkhauser Verlag, Basel , 1978, 116: 615-626. |
| [4] | 周惠兰. 地球内部物理. 北京: 地震出版社, 1990 . Zhou H L. Physics of the Earth's Interior (in Chinese). Beijing: Seismological Press, 1990 . |
| [5] | 罗丽, 何昌荣. 热水条件下斜长石和辉石断层泥的摩擦滑动研究. 地震地质 , 2009, 31(1): 84–96. Luo L, He C R. Frictional sliding of pyroxene and plagioclase gouges under hydrothermal conditions. Seismology and Geology (in Chinese) , 2009, 31(1): 84-96. |
| [6] | Dieterich J H. Modeling of rock friction:1. Experimental results and constitutive equations. J. Geophys. Res. , 1979, 84: 2161-2168. |
| [7] | Ruina A L. Slip instability and state variable friction laws. J. Geophys. Res. , 1983, 88: 10359-10370. DOI:10.1029/JB088iB12p10359 |
| [8] | Linker M F, Dieterich J H. Effects of variable normal stress on rock friction:observations and constitutive equations. J. Geophys. Res. , 1992, 97: 4923-4940. DOI:10.1029/92JB00017 |
| [9] | Beeler N M, Tullis T E. The role of time and displacement in the evolution effect in rock friction. Geophys. Res. Lett. , 1994(21): 1987-1990. |
| [10] | Dieterich J H, Kilgore B D. Direct observation of frictional contacts:new insights for state-dependent properties. Pure Appl. Geophys. , 1994, 143: 283-302. DOI:10.1007/BF00874332 |
| [11] | Dieterich J H. Earthquake nucleation on faults with rate-and state-dependent strength. Tectonophysics , 1992, 211: 115-134. DOI:10.1016/0040-1951(92)90055-B |
| [12] | Tse S T, Rice J R. Crustal earthquake instability in relation to the depth variation of frictional slip properties. J. Geophys. Res. , 1986, 91(B9): 9452-9472. DOI:10.1029/JB091iB09p09452 |
| [13] | Lockner D A, Summers R, Byerlee J D. Effects of temperature and sliding rate on frictional strength of granite. Pure Appl. Geophys. , 1986, 124: 445-469. DOI:10.1007/BF00877211 |
| [14] | Blanpied M L, Lockner D A, Byerlee J D. Fault stability inferred from granite sliding experiments at hydrothermal conditions. Geophys. Res. Lett. , 1991, 18(4): 609-612. DOI:10.1029/91GL00469 |
| [15] | Blanpied M L, Lockner D A, Byerlee J D. Frictional slip of granite at hydrothermal conditions. J. Geophys. Res. , 1995, 100(B7): 13045-13064. DOI:10.1029/95JB00862 |
| [16] | Chester F M, Higgs N G. Multimechanism friction constitutive model for ultrafine quartz gouge at hypocentral conditions. J. Geophys. Res. , 1992, 97(B2): 1859-1870. DOI:10.1029/91JB02349 |
| [17] | He C, Wang Z, Yao W. Friction sliding of gabbro under hydrothermal conditions. Tectonophysics , 2007, 445: 353-362. DOI:10.1016/j.tecto.2007.09.008 |
| [18] | He C, Yao W, Wang Z, et al. Strength and stability of frictional sliding of gabbro gouge at elevated temperatures. Tectonophysics , 2006, 427: 217-229. DOI:10.1016/j.tecto.2006.05.023 |
| [19] | 谭文彬, 何昌荣. 高温高压及干燥条件下斜长石和辉石断层泥的摩擦滑动研究. 地学前缘 , 2008, 15(3): 279–286. Tan W B, He C R. Frictional sliding of pyroxene and plagioclase gouges in gabbro under elevated temperature and dry conditions. Earth Science Frontiers (in Chinese) , 2008, 15(3): 279-286. |
| [20] | 罗丽. 热水条件下斜长石和辉石断层泥的摩擦滑动研究. 北京: 中国地震局地质研究所, 2008 . Luo L. Frictional sliding of pyroxene and plagioclase gouges under hydrothermal conditions (in Chinese). Beijing: Institute of Geology, China Earthquake Administration, 2008 . |
| [21] | 黄建国, 张流. 三轴试验中斜向摩擦面积、应力的修正法. 地震地质 , 2000, 22(3): 316–317. Huang J G, Zhang L. Correction method for axial stress in the triaxial friction experiment. Seismology and Geology (in Chinese) , 2000, 22(3): 316-317. |
| [22] | 何昌荣, 陶青峰, 王泽利. 高温高压条件下辉长岩的摩擦强度及其速率依赖性. 地震地质 , 2004, 26(3): 450–460. He C R, Tao Q F, Wang Z L. Frictional strength and rate dependence of gabbro under elevated temperature and pressure. Seismology and Geology (in Chinese) , 2004, 26(3): 450-460. |
| [23] | Rutter E H. On the nomenclature of mode of failure transitions in rocks. Tectonophysics , 1986, 122: 381-387. DOI:10.1016/0040-1951(86)90153-8 |
 2010, Vol. 53
2010, Vol. 53