2. 中国科学院地质与地球物理研究所, 北京 100029;
3. 国家卫星气象中心遥感应用试验基地/广西气象减灾研究所, 南宁 530022;
4. 中国气象科学研究院, 北京 100081
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. Remote Sensing Application and Experiment Station of National Satellite Meteorological Center/Guangxi Meteorological Disaster Mitigation Institute, Nanning 530022, China;
4. Chinese Academy of Meteorological Sciences, Beijing 100081, China
地磁场水平梯度图反映的是地磁场水平梯度沿南北方向和东西方向的分布特征,将它与地磁图相结合,可更好地揭示地磁场的空间分布特点、研究地磁场的空间变化,并可用于分析和指导地磁观测网的建设等领域,对地磁场的理论研究和实际应用具有重要的参考价值和应用前景.
地磁场模型是研究地磁场和水平梯度的基础,它可分为全球模型和区域模型.全球模型一般以国际地磁参考场(IGRF)为代表,自1968年起,国际地磁与高空物理学协会(IAGA)给出了以5年为间隔的IGRF[1~7],现已发布了最新的第11代(IGRF11),它包含了1900~2010年的23个主磁场模型以及2010~2015年的长期变化模型,现可在网站(http://www.ngdc.noaa.gov/IAGA/vmod/igrf.html)下载,另外还有计算精度较高的CHAOS模型系列,CM模型系列等[8~14].对于区域地磁场模型的研究,各国学者利用Taylor多项式、矩谐分析、球冠谐分析、曲面Spline、自然正交分量(NOC)等多种方法,得到了各个国家与区域的地磁场模型[15~22],其中Gaya-Piqué等利用球冠谐模型建立了南极地区地磁场模型[23].顾左文等于2009年利用NOC方法,基于1995~2006年中国地区的地磁测量数据进行了空间域、时间域的本征向量计算,并与中国地磁模型进行了对比分析[24].中国地震局分别于2005、2010年对中国地磁图做了大量工作.
对于中国地区地磁场水平梯度的分布,安振昌曾利用国际地磁参考场进行了相关研究[25, 26].本文考虑采用Taylor多项式方法和曲面Spline方法建立中国地区地磁场模型.这两种方法各有特点,Taylor多项式方法具有计算简单、使用方便的特点,并能够较好地表示地磁场大尺度的时空变化特征[27],而曲面Spline方法是基于过点插值的原理,能够较好地反映区域地磁场小尺度的分布特征.通过建立以上两种模型,利用微分法可计算和绘制中国地区地磁场水平梯度图.由于IGRF10仍是现在较为常用的主磁场模型,因此将2000年IGRF10的水平梯度图与Taylor水平梯度图相比较验证,最后分析3分量F、D、I水平梯度的分布情况.
2 数据及其处理本文所用资料为2000年中国地区117个地磁复测点和39个地磁台站的三分量F、D、I绝对观测数据,考虑到计算范围会涉及境外地区,选取了日本柿冈、俄罗斯库尔斯克等周边国家的6个地磁台站参与计算,数据来源于中国科学院地质与地球物理研究所以及INTERMAGNET网站(http://www.intermagnet.org/).测点分布范围:18°N~54°N;72°E~145°E.
由于境外地磁数据较少,且考虑到对边界效应的控制,同时计算结果应与IGRF模型分布趋势保持一致,因此在中国境外地区均匀选取了36个IGRF10的数值点[28].实际共198个数据点参与计算,其中国内实测点156个,国外地磁台站6个,境外IGRF计算点36个(见图 1).

|
图 1 2000年中国大陆及邻近地区地磁测点分布图 Fig. 1 Distribution chart of geomagnetic stations over China and adjacent area for 2000 |
为了计算地磁场的水平梯度,必须首先建立地磁场的数学模型.徐文耀曾利用泰勒多项式方法编绘了中国地区的地磁图[29],本文利用相同的方法,同时还使用了曲面Spline方法建立中国地区地磁场模型.
3.1 地磁场Taylor多项式及其水平梯度模型地磁场在空间的分布具有连续性,故可进行Taylor展开.其表达式为:
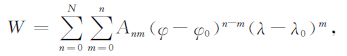
|
(1) |
式中W为任意地磁分量;N为截断阶数,本文在比较各阶均方偏差以及水平梯度的边界分布情况后,取N=4;φ、λ为各地磁测点的纬度和经度;φo、λo为多项式的展开原点,φo=36.0°N,λo=104.5°E;Anm为相应各分量的模型系数,每个模型有(N+1)(N+2)/2个系数,所有系数通过最小二乘法求取.
基于Taylor多项式模型以及微分原理,通过对模型中的φ和λ进行微分,得到F、D、I的水平梯度表达式:
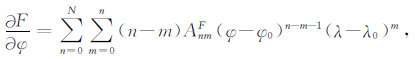
|
(2) |
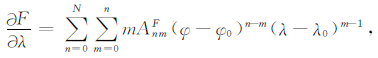
|
(3) |
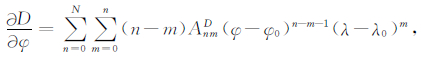
|
(4) |
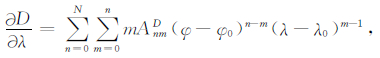
|
(5) |

|
(6) |
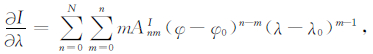
|
(7) |
其中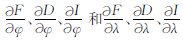
曲面Spline模型的表达式如下所示:
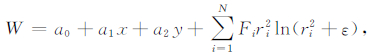
|
(8) |
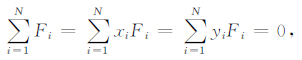
|
(9) |
其中,W为任意地磁分量;x为纬度,y为经度;ri2=(xi-x)2 +(yi-y)2;N为测点数;a0、a1、a2和Fi为需求系数;ε为控制表面曲率变化的小量,取值为1×10-7,共有N+3个系数.地磁场的强度单位:纳特(nT),角度单位:角度(°).
通过对曲面Spline模型中的x和y进行微分,得到水平梯度表达式:
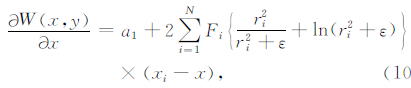
|
(10) |
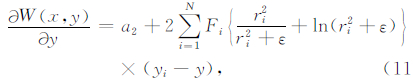
|
(11) |
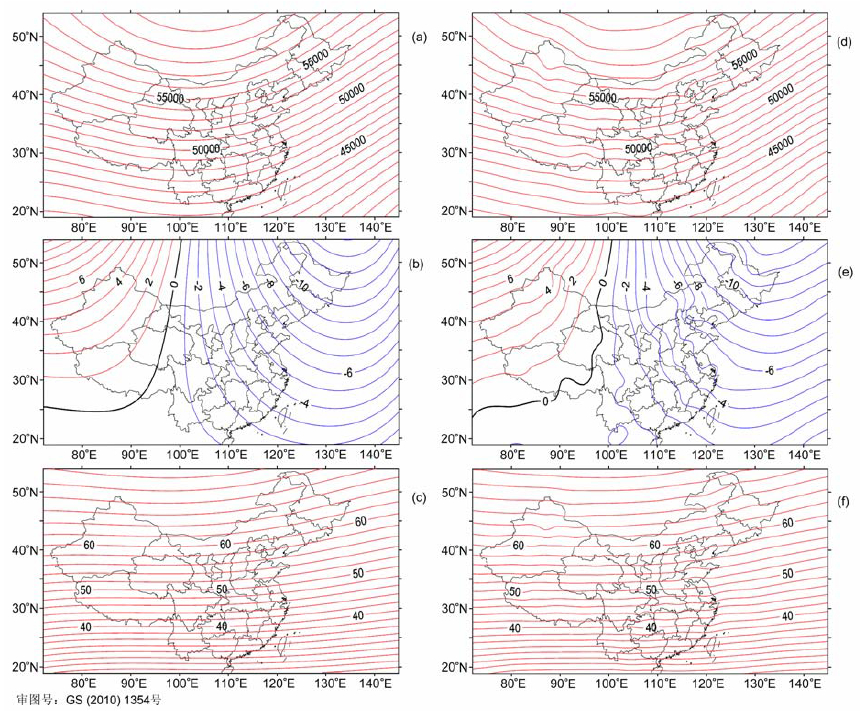
利用Taylor多项式和曲面Spline模型,分别绘制出3分量2000年中国地区地磁图(见图 2).
|
图 2 2000年中国大陆地区地磁图 (a)F(nT),(b)D(°),(c)I(°)(基于Taylor模型),(d)F(nT),(e)D(°),(f)I(°)(基于曲面Spline模型) Fig. 2 Geomagnetic charts in China for 2000 (a, b, c) Based on Taylor model; (d, e, f) Based on Surface Spline model. |
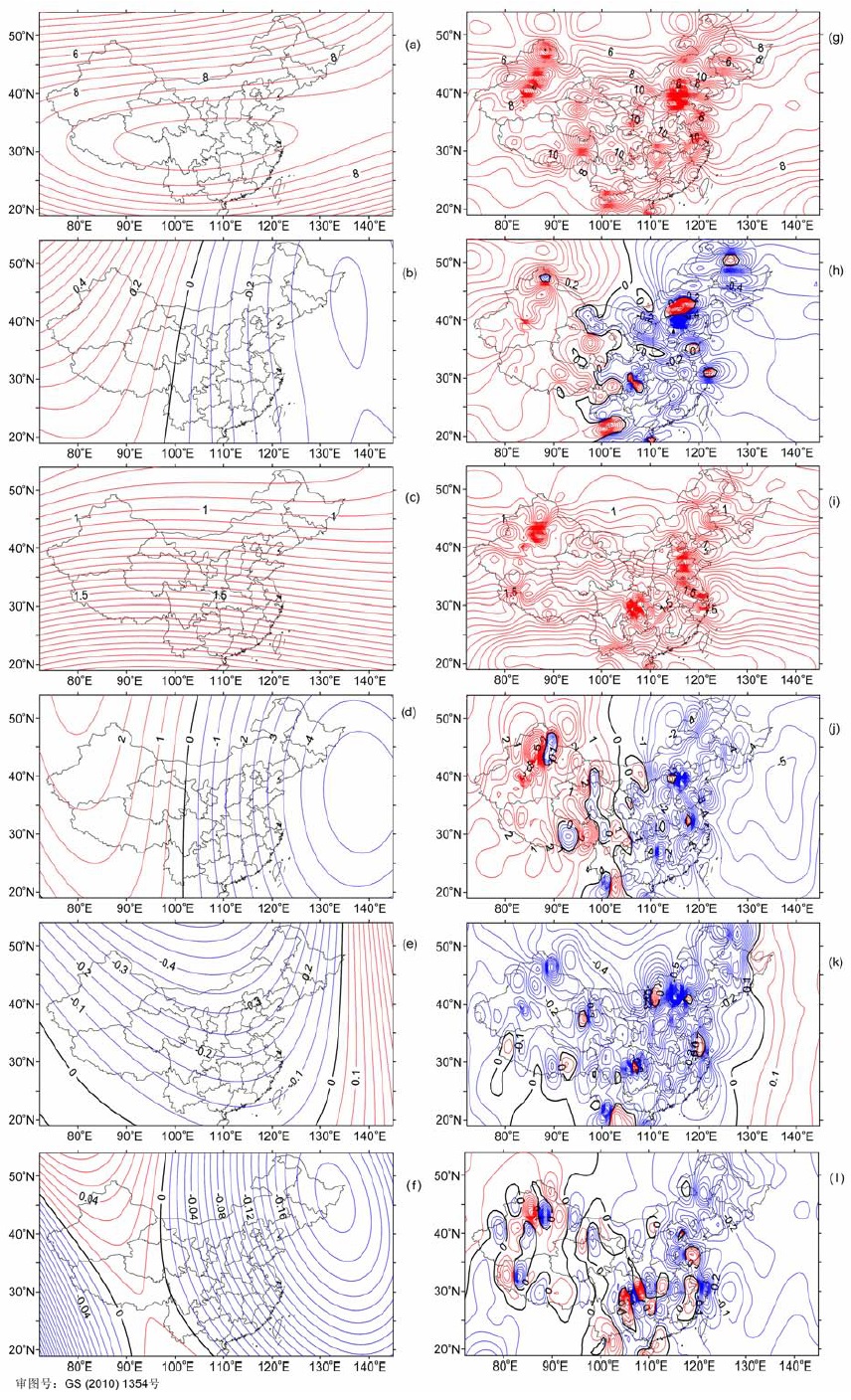
对于两种模型利用微分方法计算并绘制出2000年中国地区地磁场F、D、I分量沿南北方向和东西方向的水平梯度图(见图 3).
|
图 3 2000年中国地图地磁场水平梯度分布图 (a)F(nT/min),(b)D(′/min),(c)I(′/min)基于Taylor模型沿南北方向梯度分布图;(d)F,(e)D,(f)I(单位同上)基于Taylor模型沿东西方向梯度分布图;(g)F,(h)D,(i)I(单位同上)基于Spline模型沿南北方向梯度分布图;(j)F,(k)D,(l)I(单位同上)基于Spline模型沿东西方向梯度分布图. Fig. 3 Horizontal gradient charts of geomagnetic field in China for 2000 (a) (nT/ min), (b, c) I('/min) South-north gradient figures byTaylor model; d,e,f) (Unit as above) East-west gradient figures by Taylor model; (g, h, i) (Unit as above) South-north gradient figures by Spline model; (j, k, l) (Unit as above) East-west gradient figures by Splinemodel. |
由图 3a和图 3g可见,F在南北方向上的水平梯度主要随纬度变化,其强度随纬度增加,变幅约为7.0~6.0nT/min,在中部地区(25°N~35°N,90°E~120°E)强度较大,为10.0nT/min左右,向南向北均逐渐减小,在新疆中部和京津地区出现较大的正异常.由图 3(d,j)可见,F沿东西方向的水平梯度主要随经度变化,其强度随经度增加,变幅约为2.0~-4.0nT/min,在新疆北部地区、京津地区附近以及西藏东南部分别有正异常和负异常.
由图 3(b、h)可见,D沿南北方向的水平梯度主要随经度变化,其强度随经度增加,变幅约为0.4′/min~-0.3′/min,随纬度变化很小,在京津地区有较大的正异常和负异常.由图 3(e、k)可见,D沿东西方向的水平梯度随纬度变化,其强度随纬度增加,变幅约为-0.1′/min~-0.4′/min.由图 3(c、i)可见,I沿南北方向的水平梯度主要随纬度变化,其强度随纬度增加,变幅约为2′/min~1′/min.由图 3(f、l)可见,I沿东西方向的水平梯度呈现鞍型场分布,新疆西北部为高值区,梯度为0.04′/min,存在正负异常;100°E、20°N附近为次高值区;中国东北部为低值区,梯度最低为-0.2′/min左右;西南为次低值区;中部为均值区,梯度为0′/min,在云贵川部分区域及福建沿海区域存在连续分布的正负梯度异常.
由图 2、3可见,两种地磁图和梯度图的整体分布基本一致,但有明显的局部差异,这主要由两种模型所表示的地磁场场源以及建模方法不同所致.从场源方面看,Taylor模型表示的是地核场以及部分长波长地壳场(地壳深层部分),故只表示了部分磁异常,而曲面Spline方法表示了地磁场的所有内源场,并能够很好地表示出许多局部地区地壳浅层的磁异常信息,而这些浅层磁异常随着不同空间而发生变化,因此造成了等值线图中正负异常较多且凌乱的现象;从建模方法看,Taylor模型是基于数值拟合的原理建模,因此绘制的图形较为平滑;而曲面Spline方法利用过点插值的方法建模,因此绘制的图形其等值线较为弯曲.造成两种异常的另一原因是实测点(台站和复测点)的数量、精度及分布情况,这些因素都对模型(尤其是对Spline模型)的精度和最后的分布产生影响,测点数量越多,精度越高,分布越密,则模型越准确、精度越高.经过梯度比较以及境外台站和IGRF点的加入计算,认为所得的计算结果基本可靠,可较为直观地展现我国地磁场3分量水平梯度的分布特征.
尽管本文使用了2000年中国境内和境外共198个数据点进行水平梯度的计算,但由于测点有限且分布不均,尤其中国东部地区测点较密,而西部地区测点数相对偏少,另外国外邻近地区台站太少,导致了梯度分辨率不是很高.本文的主要目的只是想展示3分量D、F、I在中国境内的水平梯度分布,今后如有条件,可适当地加密测量,并尽可能多地利用境外实测点数据,从而建立较为理想的模型.
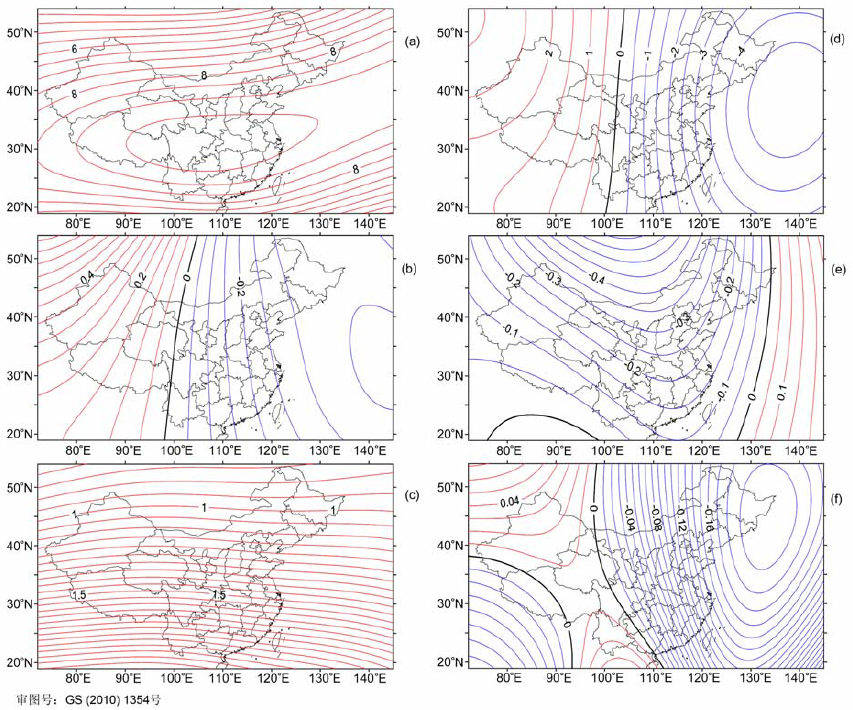
4.2.2 基于IGRF10模型的地磁场水平梯度图为了验证以上两种模型所绘制的水平梯度的可靠性,并进行比较,我们基于IGRF10,绘制了2000年中国地区的水平梯度图(见图 4).
|
图 4 2000年基于IGRF模型的中国地区地磁场水平梯度分布图 (a)F(nT/min);(b)D(′/min);(c)I(′/min)沿南北方向梯度分布;(d)F;(e)D;(f)I(单位同上)沿东西方向梯度分布. Fig. 4 Distribution charts of Geomagnetic field horizontal gradients based on IGRF inChinafor 2000 (a) F(nT/ min); b) D(Vmin); (c) J(V min) Figures of south-north direction gradient; (d) F; (e) D; , (f) I(Unit as above) Figures of east-west direction gradient. |
经对比分析,基于Taylor模型的梯度图与基于IGRF10的梯度图在分布趋势和强度特征方面都基本一致,但是两种图形在局部区域(边和角区域)还存在一定差异,这主要是由于两种模型代表的场源不同,IGRF所代表的主要是地核场部分,而Taylor模型不仅能表示地核场,还能表示部分长波长地壳场的能量,故所绘制梯度图的分布和极值强度略有不同,因此,使用区域模型所得出的水平梯度相对于IGRF能反映更多的信息,从而具有更多的实用价值.
5 结论通过对3种模型水平梯度的比较分析,得出以下结论:
(1)从水平梯度的整体分布趋势看,总强度F和磁倾角I的水平梯度主要随纬度变化,F强度随纬度增加,变幅约为7.0~6.0nT/min,在中部地区(25°~35°N,90°~120°E)强度达到最大;I随纬度的增加,变幅约为2′/min~1′/min;D的水平梯度随纬度和经度而变化,随着经度和纬度的增加,变幅分别约为0.4′/min~-0.3′/min和-0.1′/min~-0.4′/min.对两种模型绘制的梯度图以及2000年IGRF水平梯度图进行比较,能反映三种水平梯度图的一致性和差异性.
(2)通过基于曲面Spline模型绘制的梯度图发现,由于2000年地磁测量点较少,且分布不均,导致了局部分布异常且可能会导致模型精度下降.今后若条件许可,可适当增加国境内外的地磁测量点,以保证模型的精度.研究梯度分布及异常对掌握地磁场水平梯度的分布规律、地磁导航、探矿、合理布设地磁测点等具有一定的指导意义[30].
(3)利用上述两种方法建立模型在只添加6个境外台站时,由于数量偏少,导致模型出现一定程度的边界效应.当在国境外均匀选取36个IGRF数据点参加计算后,边界效应得到了很好的控制.
(4)研究地磁场的水平梯度变化,有助于深入研究地磁场的空间变化,也是计算高空地磁场和建立三维地磁场模型的基础.地磁总强度F在南北方向的水平梯度在我国中部地区为最大值,这一现象可能与地球内部物质的组成和运动状况有关,需要进一步研究.
| [1] | IA GA, Commission 2, Working Group 4. International geomagnetic reference field 1965.0. J.Geophys.Res , 1969, 74: 4407-4408. DOI:10.1029/JB074i017p04407 |
| [2] | IA GA, Division 1, Working Group 1. International geomagnetic reference field revision 1985. J. Geomag.Geoelectr. , 1985, 37: 1157-1163. DOI:10.5636/jgg.37.1157 |
| [3] | Barton C E. International geomagnetic reference field:the seventh generation. J. Geomag. Geoelectr. , 1997, 49(1): 123-156. |
| [4] | Mandea M, Macmillan S. International geomagnetic field-the eighth generation. Earth Planet Space. , 2000, 52(12): 1119-1124. DOI:10.1186/BF03352342 |
| [5] | IA GA, Division V, Working Group 8. The 9th generation international geomagnetic reference field. Geophys. J. Int. , 2003, 155: 1051-1056. DOI:10.1111/gji.2003.155.issue-3 |
| [6] | IA GA, Division V, Working Group 8. International geomagnetic reference field 2000. Geophys.J.Int. , 2000, 141: 259-262. DOI:10.1046/j.1365-246x.2000.00121.x |
| [7] | Maus S, Macmillan S, Chernova T, et al. IAGA Division V, Working Group VMOD. The 10th Generation International Geomagnetic Reference Field. Phys. Earth Planet. Inter. , 2005, 151: 320-322. |
| [8] | Olsen N, Luhr H, Sabaka T J, et al. CHAOS-a model of Earth's magnetic field derived from CHAMP, ørsted, and SAC-C magnetic satellite data. Geophys. J. Int. , 2006, 166: 67-75. DOI:10.1111/gji.2006.166.issue-1 |
| [9] | Olsen N, Mandea M, Sabaka T J, et al. CHAOS-2--A geomagnetic field model derived from one decade of continuous satellite data. Geophys. J. Int. , 2009, 179: 1477-1487. DOI:10.1111/gji.2009.179.issue-3 |
| [10] | Langel R A, Sabaka T J, Baldwin R T, et al. The near Earth magnetic field from magnetospheric and quiet-day ionospheric sources and how it is modeled. Phys Earth Planet Int. , 1996, 98(324): 235-267. |
| [11] | Sabaka T J, Olsen N, Langel R A. A comprehensive model of the quiet-time, near-Earth magnetic field:phase 3. Geophys. J. Int. , 2002, 151: 32-68. DOI:10.1046/j.1365-246X.2002.01774.x |
| [12] | Sabaka T J, Olsen N, Purucker M E. Extending comprehensive models of the Earth's magnetic field with Oersted and CHAMP data. Geophys. J. Int. , 2004, 159: 521-547. DOI:10.1111/gji.2004.159.issue-2 |
| [13] | Maus S, Sazonova T, Hemant K, et al. National geophysical data center candidate for the world digital magnetic anomaly map. Geochem. Geophys. Geosyst. , 2007, 8(6). DOI:10.1029/2007GC001643 |
| [14] | Maus S, Luhr H, Rother M, et al. Fifth-generation lithospheric magnetic field model from CHAMP satellite measurements. Geochem. Geophys. Geosyst. , 2007, 8(5). DOI:10.1029/2006GC001521 |
| [15] | Alldredge L. Rectangular harmonic analysis applied to the geomagnetic field. J. Geophys.Res. , 1981, 86(B): 3021-3026. |
| [16] | 徐文耀, 朱岗崑. 我国及邻近地区地磁场的矩谐分析. 地球物理学报 , 1984, 27(6): 511–522. Xu W Y, Tschu G K. A study of the RHA for the geomagnetic field of China and neighbouring region. Chinese J.Geophys. (in Chinese) , 1984, 27(6): 511-522. |
| [17] | 安振昌, 徐元芳, 夏国辉, 等. 表示局部地区地磁场及其长期变化分布的数学方法. 地球物理学报 , 1982, 25(Suppl.): 711–717. An Z C, Xu Y F, Xia G H, et al. Mathematical methods to express the distribution of geomagnetic field and its secular variation in a local area. Chinese J.Geophys. (in Chinese) , 1982, 25(Suppl.): 711-717. |
| [18] | Haines G V. Spherical cap harmonic analysis. J. Geophys. Res. , 1985, 90(B3): 2583-2592. DOI:10.1029/JB090iB03p02583 |
| [19] | Kote M, Haok V. Modeling European magnetic repeat station and survey data by SCHA in search of time-variation anomalies. Phys. Earth Planet.Inter. , 2000, 122(3-4): 205-220. DOI:10.1016/S0031-9201(00)00194-1 |
| [20] | 顾左文, 安振昌, 高金田, 等. 京津冀地区地磁场球冠谐分析. 地球物理学报 , 2004, 47(6): 1128–1134. Gu Z W, An Z C, Gao J T, et al. Spherical cap harmonic analysis on the geomagnetic field in Beijing-Tianjin-Hebei region. Chinese J.Geophys. (in Chinese) , 2004, 47(6): 1128-1134. DOI:10.1002/cjg2.v47.6 |
| [21] | 高金田, 安振昌, 顾左文, 等. 地磁正常场的选取与地磁异常场的计算. 地球物理学报 , 2005, 48(1): 51–62. Gao J T, An Z C, Gu Z W, et al. Selections of geomagnetic normal field and calculations of geomagnetic anomalous field. Chinese J.Geophys. (in Chinese) , 2005, 48(1): 51-62. |
| [22] | Burdelnay I A, Filippov S V, Golovkov V P, et al. Regional orthogonal models of the geomagnetic field changes over the Far East. Earth Planet Space. , 1999, 51(4): 287-296. DOI:10.1186/BF03352232 |
| [23] | Gaya-Piqué L R, Santis A D, Torta J M. Use of Champ Magnetic Data to Improve the Antarctic Geomagnetic Reference Model, Earth Observation with CHAMP. Germany: Springer Berlin Heidelberg, 2005 . |
| [24] | 顾左文, 陈斌, 高金田, 等. 应用NOC方法研究中国地区地磁时空变化. 地球物理学报 , 2009, 52(10): 2602–2612. Gu Z W, Chen B, Gao J T, et al. Research of geomagnetic spatial-temporal variations in China by the NOC method. Chinese J.Geophys. (in Chinese) , 2009, 52(10): 2602-2612. |
| [25] | 安振昌. 地磁场水平梯度的计算与分析. 地球科学进展 , 1992, 7(1): 39–43. An Z C. Calculation and analyses of the horizontal gradient of the geomagnetic field. Advance in Earth Sciences (in Chinese) , 1992, 7(1): 39-43. |
| [26] | 安振昌. 地磁总强度梯度的计算与分布. 物探与化探 , 1992, 16(5): 365–369. An Z C. Calculation and analyses of the gradient of the total geomagnetic intensity. Geophysical & Geochemical Exploration (in Chinese) , 1992, 16(5): 365-369. |
| [27] | 夏国辉, 郑双良, 吴莉兰, 等. 1980年代中国地磁正常场图及其数学模式. 地球物理学报 , 1988, 31(1): 82–89. Xia G H, Zheng S L, Wu L L, et al. The geomagnetic field maps of China in 1980.0 and the mathematical model. Acta Geophysica Sinica (in Chinese) , 1988, 31(1): 82-89. |
| [28] | Gu Z W, An Z C, Gao J T, et al. Computation and analysis of the geomagnetic field model in China and its adjacent area for 2003. Acta Seismologica Sinica , 2003, 19(2): 145-154. |
| [29] | Xu W Y, Xia G H, An Z C, et al. Magnetic survey and ChinaGRF 2000. Earth Planets Space. , 2003, 55: 215-217. DOI:10.1186/BF03351750 |
| [30] | Newitt L R, Barton C E, Bitterly J.地磁复测点测量指南.李琪, 宋彦云, 韩德胜等译.北京:地震出版社, 2002 Newitt L R, Barton C E, Bitterly J. Guide for Magnetic Repeat Station Surveys. Li Q, Song Y Y, Han D S, et al. translation. Beijing:Seismological Press, 2002 |
 2010, Vol. 53
2010, Vol. 53


