2. 中国科学院上海天文台, 上海 200030;
3. 北京航天指挥控制中心, 北京 100094
2. Shanghai Astronomical Observatory, CAS, Shanghai 200030, China;
3. Beijing Aerospace Command and Control Center, Beijing 100094, China
月球重力场是月球科学研究的一个重要部分,它是在以月球为研究对象时,考虑到它内部物质分布的不均匀性以及外部几何形状的不规则性而产生的扰动重力场.月球重力场的研究具有重要的理论意义,它是研究月球物理性质及内部结构、月球的起源与演化等科学问题最主要的手段.月球重力场是月球卫星轨道摄动的主要摄动力源,精化月球重力场对于高精度月球卫星定轨以及月球飞行器着陆同样具有相当重要的意义,也是决定月球卫星能量装备的一个重要设计指标.特别是对于我国即将发射的月球着陆器及后期的登月,高精度的重力场信息是进行准确的轨道设计、成功完成软着陆的重要保障[1].
月球重力场的研究起源于1959年前苏联发射的第一颗绕月卫星.几十年来,随着卫星数目的增加以及跟踪技术的发展,月球重力场也处于不断的完善和发展中.近期两个具有代表性的重力场模型为GLGM-2和LP165P[2],前者是GSFC(Goddard Space Flight Center)利用美国宇航局1994发射的月球探测器Clementine的跟踪数据,结合历史上Apollo系列探测器的跟踪数据,得到的70阶次的月球重力场模型.后者是JPL(Jet Propulsion Laboratory)利用美国宇航局1998年发射的月球探测器LP(Lunar Prospector)在正常任务(平均轨道高度为100km)及扩展任务阶段(平均高度为30km)共18个月的跟踪数据,以及Clementine及Apollo等历史探测器跟踪数据,解算得到的165阶次月球重力场模型,它给出了月球正面高精度高分辨率重力场信息.为了进一步利用LP探测器包含的月球正面重力场信息,Han利用局部球谐函数展开的方法对LP视向加速度数据进行了解算,得到的新模型相比于全球重力场模型在局部区域表现出与地形更强的相关性[3, 4].日本于2007年8月发射的探月计划Kaguya首次实现了对月球背面的直接测量,得到的月球重力场模型SGM90d[5, 6]与LP165P等模型[2]相比较,在月球背面重力场的精度和分辨率上有显著改进.基于SGM90d在月球背面发现了新的重力异常特征.正面的典型质量瘤区域为负的重力异常包围正的重力异常,在月球背面的典型区域,比如Korolev,则发现了重力异常的环状包围形式,即在中心区域为负的重力异常,由正的重力异常区包围,在外层又由负的重力异常区包围,正负重力异常区交错出现.这一新的重力异常特征为研究背面壳幔结构、均衡补偿状态以及月球二分性等科学问题提供了新的依据[5].月球重力场仍然是月球科学研究的重要组成部分,多个待发射的月球探测计划将月球重力场探测列为主要科学目标.美国新千年重返月球的第一个探测计划LRO(Lunar Reconnaissance Orbiter)于2009年6月发射[7],以50km高的圆极轨道在轨运行一年,主要科学目标为高精度高分辨率获取月面地形及月球重力场.2011年美国将发射月球探测计划GRAIL(Gravity Recovery and Interior Laboratory)主要用于月球重力场探测[8],这一计划以类似于GRACE(Gravity Recovery and Climate Experiment)卫星跟踪卫星的模式[9]用于高精度的月球重力场模型探测,预期精度将比日本SELENE计划得到的重力场模型SGM90d提高至少三个数量级[10].
“嫦娥一号”于2007年10月24日发射,经过调相段、地月转移段、月球捕获段和环月飞行段等多次轨道调整后,成为绕月球运动的极轨圆轨道卫星,轨道高度为200 km.“嫦娥一号”主要科学目标为获取高精度月面三维地形,得到月球表面土壤成分及各矿物质分布情况[1].本文根据“嫦娥一号”常规管理运行期间提供的大量轨道跟踪数据,进行了独立的月球重力场模型解算.这一工作的目的是探讨“嫦娥一号”用于月球重力场模型解算的可行性及解算流程的可靠性,为综合历史已有的及最新的“嫦娥一号”、SELENE等探测器的轨道跟踪数据进行高精度月球重力场模型解算打下基础,研究“嫦娥一号”轨道跟踪数据在高精度月球重力场模型解算中的贡献,为我国开展月球重力场探测提供一定参考.在此工作上更新“嫦娥一号”探测器轨道星历,提高基于激光高度计的地形模型精度,为综合地形重力开展月壳厚度、月球岩石圈弹性厚度等月球内部构造方面的研究工作提供更好的地形数据支撑.解算平台以GEODYNII/SOLVE为基础[11, 12],并结合了大量的独立开发.
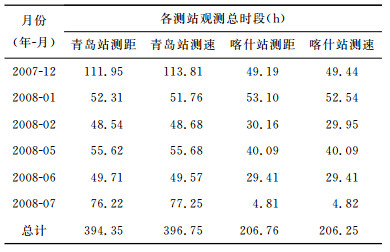
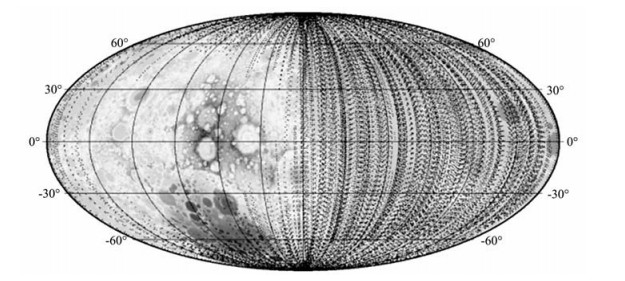
2 CEGM-01重力场模型解算文中月球重力场模型CEGM-01解算利用的“嫦娥一号”跟踪数据为青岛和喀什两测控站的双程测距测速数据.数据采样率为1 s,测控单位提供的测距测速标称精度分别为2 m和10 mm·s-1.精密定轨和重力场模型解算中根据实际的观测量残差进行定权,测距测速权重分别为1 m和10 mm·s-1.测速权重值略大于其测量残差,这是因为测站频率基准精度有限等原因导致测速存在比较明显的系统偏差,为了降低其对重力场模型解算的影响,弱化了测速数据的权重.常管期间2007年12月每天观测弧段约为6h,2008年1月、2月每天观测弧段约为3h,3月、4月没有观测数据,5月、6月、7月每天观测弧段约为3h,轨道跟踪数据星下点在月面的覆盖情况见图 1.重力场模型解算利用到的6个月总的观测弧段长度如表 1所示.由于月球天平动效应以及部分弧段通视跟踪测量,跟踪数据可以覆盖月球背面和两极部分区域.
|
图 1 “嫦娥一号”轨道跟踪数据星下点覆盖图(左边为月球背面,右边为月球正面) Fig. 1 Subsatellite point distribution of Chang′E-1 orbital tracking data (left is lunar farside, right is lunar nearside) |
|
|
表 1 各测站观测总弧段 Table 1 Total observational arcs of each station |
解算之前对观测数据进行了平滑滤波处理,扣除了电离层和中性大气的影响.解算过程中考虑到的动力学模型有月球非球形引力摄动、地球和太阳及其他大行星的三体摄动、地球扁率的间接摄动、太阳光压摄动等.由于“嫦娥一号”轨道较高,计算中选取的弧段长度为一天,可以不用考虑月面反射压摄动的影响[13].文中采用的先验重力场模型为GLGM-2[14],采用它是因为这个模型是以Clementine的轨道跟踪数据为主,综合了历史上月球探测器的轨道跟踪数据解算得到的.Clementine轨道器为极轨大偏心率轨道,近月点高度为2162km,远月点高度为4594 km,由Clementine解算得到重力场模型GLGM-2可以较好地反映月球重力场中低阶次位系数信息.为了降低GLGM-2高阶项位系数对嫦娥重力场模型解算的影响,计算过程中GLGM-2模型与求解的CEGM-01模型阶次相同,均取至50阶次.“嫦娥一号”200 km高度的轨道数据主要对重力场中高阶次位系数的解算有贡献,可以较好地改进GLGM-2模型.
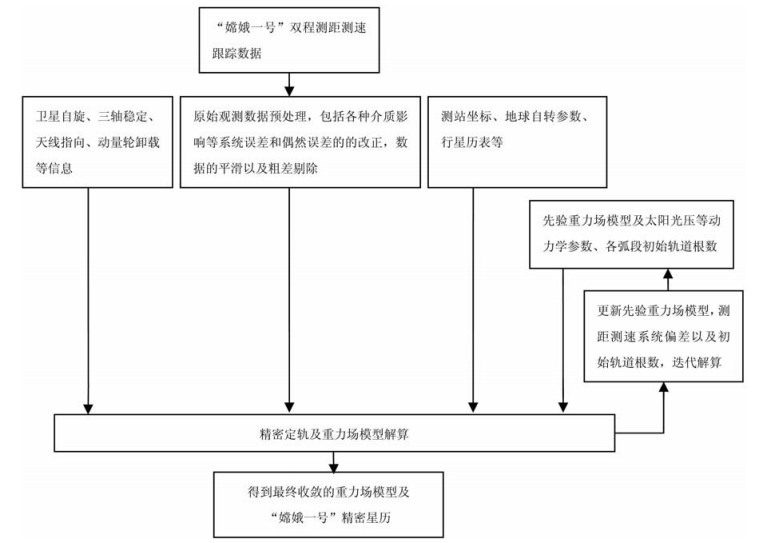
解算参数包括局部参数和全局参数.局部参数主要为各弧段卫星初始轨道根数、每个站每个跟踪弧段测距测速系统偏差(主要用于补偿介质改正模型的不完善以及地面本振信号的频漂)、用于模制卫星动量轮卸载的经验加速度常数分量[14].由于每个弧段跟踪时间较短,太阳光压系数没有参与估计,直接采用先验光压模型.全局参数为月球重力场位系数,解算阶次为2阶次至50阶次.由于“嫦娥一号”卫星高度以及跟踪弧段长度的限制,CEGM-01模型解算的阶次定为50阶次.解算中,考虑到比较频繁的动量轮卸载对重力场解算的影响,进行精密定轨的弧段选取为一天,最大程度地降低非模型化的力对精密定轨及重力场模型解算的影响.由于测站及跟踪弧段均有限制,无法通过几何法定轨得到“嫦娥一号”的精密轨道.文中以月心参考系下卫星运动的动力学方程为基础,结合变分方程,利用动力法进行精密定轨与重力场模型解算[2, 14].每个弧段生成观测量对重力场位系数的偏导数构成法方程矩阵,最后综合各弧段的法方程矩阵进行重力场位系数的统一解算.图 2给出了利用“嫦娥一号”轨道跟踪数据进行月球重力场模型解算的流程图.
|
图 2 基于“嫦娥一号”跟踪数据进行月球重力场模型解算流程 Fig. 2 Lunar gravity field solution diagram based on tracking data of Chang′E-1 |
解算中利用到的惯性参考系为月心J2000坐标系统[15],到月固系的转换所用到的欧拉角信息由DE403提供[16],同时DE403也用于在计算三体摄动时确定地球、太阳及其他天体的位置.
3 CEGM-01重力场模型功率谱月球重力场球谐函数模型位系数的阶方差信息可以反映重力场在频域中的信号强度,而误差阶方差则用来反映重力场在频域中误差的强度,可以表示重力场模型的形式误差.阶方差σn与误差阶方差δn的计算公式分别为[17, 18]:
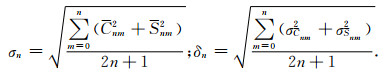
|
(1) |
式中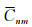
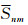
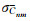

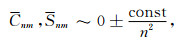
|
(2) |
对于月球重力场解算常数const可取值为1.5× 10-4.在月球重力场模型确定中引入Kaula准则的目的是作为一个正则化因子,用来克服由于月球背面数据缺乏导致对重力场求解时的不稳定性,同时对高阶解的计算起到一平滑作用[18].
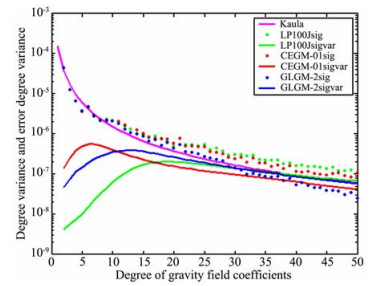
图 3给出了Kaula曲线和三个月球重力场模型位系数阶方差与误差阶方差曲线图,图中sig和sigvar分别表示阶方差和误差阶方差.由图 3可以看出,GLGM-2模型25阶次之后的位系数阶方差小于误差阶方差,说明该模型在这一阶次之后的信息量小于噪声,这一阶次之后的信息主要是通过数学约束解算得到,不包含实际的月球重力场信息. LP100J综合了LP探测器100 km正常轨道运行期间和扩展任务阶段三个月的跟踪数据,以及Clementine和早期历史跟踪数据.由图 3可以看出,LP100J和GLGM-2在低阶次部分一致度较高,这是因为两个模型用于求解中长波位系数的跟踪数据源一致.由于LP100J模型求解时用到了大量的低轨跟踪数据,20阶次之后LP100J比GLGM-2具有更强的信号及更高的解算精度.
|
图 3 重力场模型频谱图 Fig. 3 Power spectrum of lunar gravity field |
CEGM-01模型仅利用了“嫦娥一号”轨道跟踪数据,200km轨道高度的跟踪数据主要对月球重力场中短波部分的解算起到作用.由图 3可以看出,9阶之后的信号强度在GLGM-2和LP100J之间,这与“嫦娥一号”运行轨道高度特征相吻合.由CEGM-01的误差阶方差曲线可以看出,CEGM-01相比于先验的GLGM-2,10阶次之后的精度有较为显著的提高,这也说明了我国“嫦娥一号”跟踪数据在解算月球重力场模型方面具有一定程度的贡献.CEGM-01误差阶方差在18阶次之后要小于LP100J,这主要是由于解算中引入了较强的Kaula约束引起的,而不是实际的重力场模型精度优于LP100J.
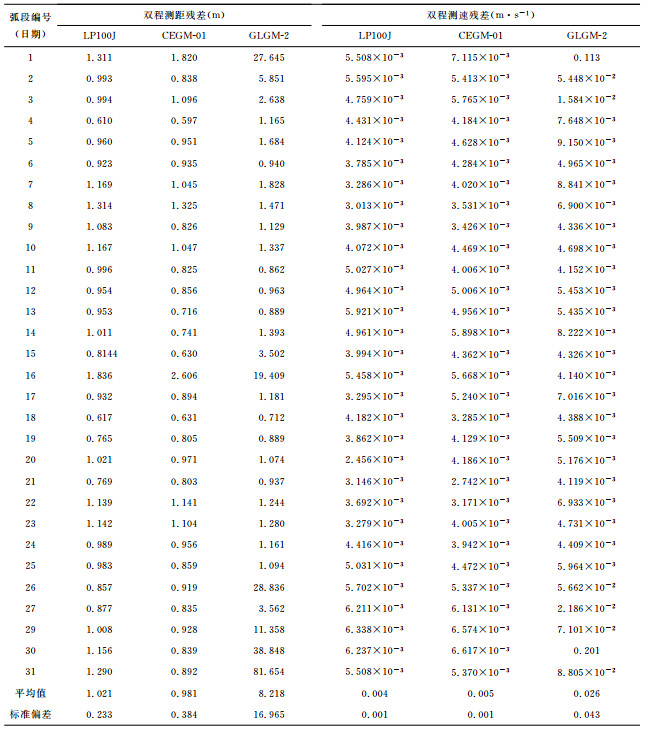
4 定轨残差分析为了进一步评价解算模型精度及可靠性,分别利用GLGM-2、LP100J和CEGM-01对6个月的跟踪弧段进行了事后精密定轨,文中主要对各测站双程测距测速跟踪数据的残差进行了比较分析.表 2给出了基于三个不同重力场模型利用测轨数据对“嫦娥一号”2008年7月逐日进行精密定轨的结果,利用GLGM-2模型对28日弧段进行精密定轨时不能收敛,故表 2中没有给出该弧段的解算结果.
|
|
表 2 2008年7月跟踪数据利用三个模型得到的测距测速残差RMS值 Table 2 RMS of range and range rate residuals of tracking data in July 2008 based on three models |
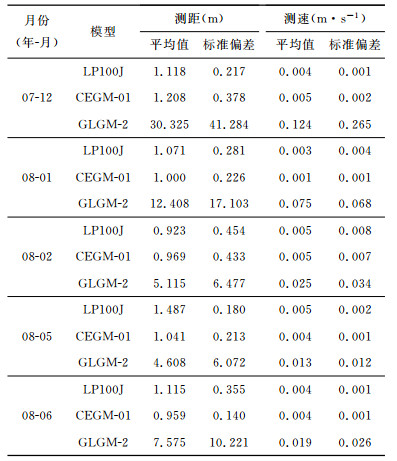
表 2给出了利用三个不同重力场模型进行精密定轨后双程测距测速的轨道残差情况,第一列表示天数,对应的残差为每个弧段中观测量残差的RMS值.由表 2的数据可以明显看出,基于三个不同重力场模型进行精密定轨,在轨道残差分布趋势上表现出比较明显的一致性,CEGM-01解算模型与LP100J模型具有比较一致的定轨精度,两者得到的残差比GLGM-2要低近一个量级.残差比较大的弧段对应于较大幅度的卫星姿态调整,或者是卫星轨道面与测站观测方向近似垂直的时段.对于后者的观测几何构型,轨道跟踪数据对卫星运动不敏感.对“嫦娥一号”其他5个月轨道跟踪数据的解算具有类似的结论,这由表 3给出的统计信息可以看出.
|
|
表 3 利用三个模型得到的测距测速残差统计信息 Table 3 Statistical information of range and range rate residuals using three models |
为了进一步分析CEGM-01的精度特征,基于为了进一步分析CEGM-01的精度特征,基于不同模型对月球表面自由空气重力异常进行了分析.月球自由空气重力异常是一个重要的重力场物理量,具有明确的物理含义.通过月球重力异常可以刻画月球内部构造的特殊性质,比如质量瘤以及月球正面和背面的二分性.综合利用最新的月球重力异常、月面地形、月球激光测距以及少量的月震信息等资料是当前月球测地学研究最主要的手段,在此基础上可以更精确地确定月球的主轴惯量矩及内部结构,为确定月核的大小与状态提供更强的约束,为月球的起源及演化等科学问题提供更客观的解释[20, 21].
基于重力场球谐级数解的月球自由空气重力异常的计算公式为[17, 22]:
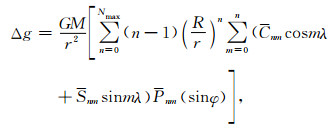
|
(3) |
式中R为月球参考球平均半径,文中取为1738 km,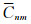

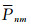
由图 4可以看出,CEGM-01与GLGM-2和LP100J相比,可以清晰地分辨出月球正面五个典型的质量异常瘤,对月球背面自由空气重力异常而言,CEGM-01比GLGM-2能分辨出更多的细节.由于跟踪数据的长度有限,以及轨道高度特征,CEGM-01在重力异常细节上的分辨能力不如LP100J.表 4给出了GLGM-2模型和CEGM-01分别与LP100J模型重力异常的相关性.
|
|
表 4 模型之间重力异常相关系数 Table 4 Correlation coefficients of gravity anomaly between models |

|
图 4 三个月球重力场模型对应的月球自由空气重力异常图(左边为月球背面,右边为月球正面) Fig. 4 Lunar free air gravity anomaly of three gravity field models (left is lunar farside, right is lunar nearside) |
由表 4可以看出,CEGM-01与GLGM-2模型相比,前者的重力异常与LP100J具有更高程度的相关性,这可以从一定程度上说明“嫦娥一号”跟踪数据有助于解析月球背面的重力场特征.
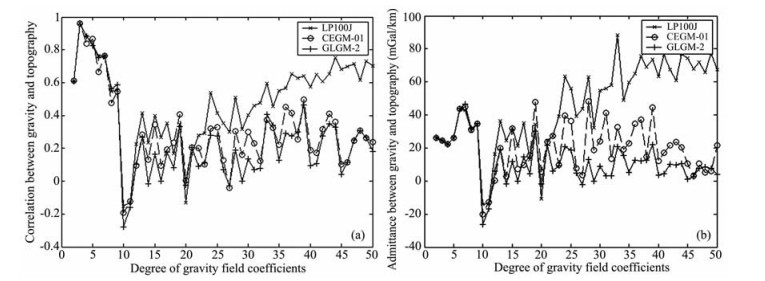
图 5给出了三个重力场模型和根据“嫦娥一号”测高数据得到的地形模型CLTM-s01[23]的相关及导纳值[24],为便于比较分析,LP100J、GLGM-2、CEGM-01与CLTM-s01均截断至50阶次.重力地形相关和导纳值是用于分析月球、火星、金星等星体内部构造、壳幔结构的一个重要工具[24],重力地形相关及导纳值与星体的弹性厚度有关,可以认为是通过给定地形负荷预测重力异常的一个转换函数[24].由图 5相关系数图可以看出,三个模型在10阶及20阶有较为显著的负相关性,这主要是由于月球质量瘤引起.此外,由图 5可以明显看出,在中短波上,CEGM-01与GLGM-2相比,相关及导纳值均有显著提高,这也说明了“嫦娥一号”轨道跟踪数据在解算月球重力场方面具有的贡献.
|
图 5 重力场模型与“嫦娥一号”地形模型相关系数(a)及导纳值(b) Fig. 5 Coherence (a) and admittance (b) between gravity field models and Chang′E-1 topography models |
文中对独立利用“嫦娥一号”轨道跟踪数据解算月球重力场模型进行了较为全面的介绍和分析,对数据源及解算原理做了简要的说明.通过重力场位系数阶方差和误差阶方差、事后精密定轨残差分析、月球自由空气重力异常及重力地形相关性与导纳分析,对解算模型的精度和可靠性进行了验证.结果表明基于“嫦娥一号”6个月的轨道跟踪数据能够较好地得到月球重力场模型,相比于先验的GLGM-2有较为明显的改善,说明了解算过程的合理性及可靠性.
“嫦娥一号”的成功实施为后续的月球探测项目积累了丰富的经验,“嫦娥一号”轨道测控数据成功用于解算月球重力场为我国开展后期具有特色的月球重力场探测试验打下了良好的基础.我国于2010年10月发射的“嫦娥二号”已成功运行,轨道高度为100km,这一高度提供的轨道跟踪数据有利于得到更高空间分辨率的重力场模型.除了降低轨道高度之外,改变倾角也是提高重力场模型精度的一个重要方面.图 6给出了利用不同倾角的轨道进行重力场仿真时得到的重力场模型对卫星定轨精度的影响(图中I为倾角).可以明显地看出,仅根据极轨卫星轨道观测数据得到的月球重力场模型,随着卫星倾角增大,轨道预报误差也随之增大.对我国后续的月球探测任务,可以考虑改变卫星轨道倾角至冻结轨道,利用这一倾角提供的轨道跟踪数据,综合已有的极轨卫星跟踪数据,有利于降低月球重力场位系数之间的相关性,减轻重力场模型误差中的条状特性[9],得到更完备的月球重力场模型.此外,在冻结轨道倾角附近处的卫星提供的激光高度计数据可以形成大量均匀分布的交叉点数据,这一数据源一方面可以验证并改进现有的月面地形模型,另外还可以对轨道面的平面及径向提供约束,结合地面测站轨道跟踪数据进行精密定轨以提高定轨精度,进而改善月球重力场模型的解算精度.

|
图 6 2个月极轨、2个月极轨+2个月77°倾角、2个月极轨+2个月77°倾角+2个月85°倾角轨道得到的月球重力场对卫星轨道月心-卫星径向精度的影响 Fig. 6 Effect on satellite radial accuracy based on gravity field models from 2 months polar, 2 months polar plus 2 month 77° inclination, 2 months polar plus 2 months 77° plus 2 months 85° inclination orbiter |
本文所提及的GEODYNⅡ/SOLVE轨道分析软件是经GSFC/NASA/USA授权中国科学院上海天文台使用,文中解算工作在上海天文台的服务器上完成.感谢北京航天指挥控制中心提供“嫦娥一号”轨道双程测距测速跟踪数据.
| [1] | 欧阳自远. 我国月球探测的总体科学目标与发展战略. 地球科学进展 , 2004, 19(3): 351–358. Ouyang Z Y. Scientific objectives of Chinese lunar exploration project and development strategy. Advance in Earth Sciences (in Chinese) , 2004, 19(3): 351-358. |
| [2] | Konopliv A S, Asmar W, Carranza E, et al. Recent gravity models as a result of the Lunar Prospect Mission. Icarus , 2001, 150(1): 1-18. DOI:10.1006/icar.2000.6573 |
| [3] | Han S C. Improved regional gravity fields on the Moon from Lunar Prospector tracking data by means of localized spherical harmonic functions. J. Geophys. Res , 2008, 113: E11012. DOI:10.1029/2008JE003166 |
| [4] | Han S C, Mazarico E, Lemoine F G. Improved nearside gravity field of the Moon by localizing the power law constraint. Geophys. Res. Lett , 2009, 36: L11203. DOI:10.1029/2009GL038556 |
| [5] | Namiki N, Iwata T, Matsumoto K, et al. Farside gravity field of the Moon from four-way Doppler measurement of SELENE (Kaguya). Science , 2009, 323(5916): 900-905. DOI:10.1126/science.1168029 |
| [6] | Goossens S, Matsumoto K, Ishihara Y, et al. Analysis of tracking data and results from Kaguya (SELENE) satellites for lunar gravity field estimation. Eos Trans, AGU, 89(53), Fall Meet. Suppl, 2008, Abstract P31B~1400 |
| [7] | Mazarico E, Lemoine F G, Neumann G A, et al. Preparations for Lunar Reconnaissance Orbiter gravity and altimetry missions. Eos Trans, AGU, 89(53), Fall Meet. Suppl., 2008, Abstract P31B~1401 |
| [8] | Zuber M. GRAIL Gravity Mission:Goals and Status. 37th COSPAR Scientific Assembly, Montréal, Canada, 2008 |
| [9] | Tapley B D, Bettadpur S, Watkins M, et al. The gravity recovery and climate experiment:Mission overview and early results. Geophys. Res. Lett , 2004, 31: L09607. DOI:10.1029/2004GL019920 |
| [10] | Hoffman T L. GRAIL:Gravity mapping the Moon. In:Proceedings of the 2009 IEEE Aerospace Conference, Big Sky, MT, USA, 7-14 March, 2009 |
| [11] | Rowlands D D, Marshall J A, Mccarthy J, et al. GEODYN Ⅱ System Description, vols. 1-5. Contractor Report, Hughes STX Corp. Greenbelt, MD, 1997 |
| [12] | Ullman R E. SOLVE program:mathematical formulation and guide to user input. Hughes/STX Contractor Report, Contract NAS5-31760. NASA Goddard Space Flight Center, Greenbelt, Maryland, 1994 |
| [13] | Floberghagen R, Visser P, Weischede F. Lunar albedo force modeling and its effect on low lunar orbit and gravity field determination. Advances in Space Research , 1999, 23(4): 733-738. DOI:10.1016/S0273-1177(99)00155-6 |
| [14] | Lemoine F G, Smith D E, Zuber M T, et al. A 70th degree lunar gravity model (GLGM-2) from Clementine and other tracking data. J. Geophys. Res , 1997, 102(16): 339-359. |
| [15] | Seidelmann P K, Archinal B A, A'Hearn M F, et al. Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements of the planets and satellites:2000. Celestial Mechanics and Dynamical Astronomy , 2002, 82(1): 83-111. DOI:10.1023/A:1013939327465 |
| [16] | Standish E M. JPL planetary and lunar ephemerides, DE405/LE405. JPL IOM 312. F-98-127, 1998 |
| [17] | Heiskanen W A, Moritz H. Physical Geodesy. San Francisco:VCH, 1967 |
| [18] | 鄢建国, 平劲松, 李斐, 等. 应用LP165P模型分析月球重力场特征及其对绕月卫星轨道的影响. 地球物理学报 , 2006, 49(2): 408–414. Yan J G, Ping J S, Li F, et al. Character analysis of the lunar gravity field by the LP165P model and its effect on lunar satellite orbit. Chinese J. Geophy. (in Chinese) , 2006, 49(2): 408-414. |
| [19] | Kaula W M. Theory of Satellite Geodesy:Applications of Satellite to Geodesy. Waltham, Mass: Blaisdell, 1966 . |
| [20] | Khan A, Mosegaard K, Williams J G, et al. Does the Moon possess a molten core? Probing the deep lunar interior using results from LLR and Lunar Prospector. J. Geophys. Res , 2004, 109: E09007. DOI:10.1029/2004JE002294 |
| [21] | 李斐, 鄢建国, 平劲松. 月球探测及月球重力场的确定. 地球物理学进展 , 2006, 21(1): 31–37. Li F, Yan J G, Ping J S. Lunar exploration and lunar gravity field determination. Progress in Geophysics (in Chinese) , 2006, 21(1): 31-37. |
| [22] | Matsumoto K, Goossens S, Ishihara Y, et al. An improved lunar gravity field model from SELENE and historical tracking data:Revealing the farside gravity features. J. Geophys. Res , 2010, 115: E06007. DOI:10.1029/2009JE003499 |
| [23] | 平劲松, 黄倩, 鄢建国. 基于嫦娥一号卫星激光测高观测的月球地形模型CLTM-s01. 中国科学G辑 , 2009, 52(7): 1105–1114. Ping J S, Huang Q, Yan J G. Lunar topographic model CLTM-s01 from Chang'E-1 laser altimeter. Science in China Series G (in Chinese) , 2009, 52(7): 1105-1114. DOI:10.1007/s11433-009-0144-8 |
| [24] | Wieczorek M A. The gravity and topography of the terrestrial planets. In:Schubert G Ed. Treatise on Geophysics. Elsevier, Amsterdam, The Netherlands.2007, vol.10 |
 2010, Vol. 53
2010, Vol. 53