2. 中国极地研究中心, 上海 200136
2. Polar Research Institute of China, Shanghai 200136, China
电磁波在尘埃等离子体中的传播问题近年来是一个受到广泛关注的研究课题.随着人类航天活动的不断增多,空间环境中的尘埃等离子体也受到越来越多的关注.高层大气中存在来自宇宙空间的和人类航天活动产生的尘埃颗粒,这些尘埃颗粒在空间环境中受周围等离子体和空间辐射的作用,形成带电颗粒,带电尘埃颗粒又通过电磁力与等离子体相互作用,形成一个复杂的电磁传播环境.由于尘埃颗粒在地球轨道空间中形成尘埃等离子体,引起的近地空间变化往往对雷达通信系统产生较大影响,所以人们很早就注意到并开始研究带电尘埃颗粒对电磁波传播的影响.有关尘埃等离子体与电磁波的相互作用近年来也取得了一些成果,地球北极极区附近的非相干雷达EISCAT (European Incoherent Scatter)己长期多次地观测到在极区上空80~90 km处的尘埃等离子体层能够对高频电磁波产生强烈的散射[1~3].Ginzburg和Tsytovich认为带电粒子的屏蔽云在电磁场中极化能产生电偶极矩辐射.根据这种散射机制,一些学者从动力论出发研究了电磁波入射尘埃等离子体的散射,并推导了电磁波的散射截面[4, 5].近期,P.Bartos等人还模拟计算了低温情况氩等离子体中尘埃粒子充电过程[6].国内也有学者在不同方面作了相关的研究,李芳对尘埃粒子引入充电频率的概念,通过求解无碰撞项的弗拉索夫方程得到尘埃等离子体的低频纵介电张量,研究等离子体中尘埃粒子对电磁波的吸收效应,分析尘埃等离子体的微波衰减特性[7, 8].在高频近似下,用玻恩近似计算散射场的微分散射截面和总散射截面,并将电子屏蔽云产生的散射与尘埃粒子产生的瑞利散射进行比较.石雁祥等则研究了尘埃粒子充放电过程对尘埃等离子体电导率的影响,并对尘埃等离子体微波衰减常数作了理论分析[9, 10].
综合分析有关含有大量尘埃粒子的高空大气中电磁波传播相关问题,国内外在此领域开展研究还较少,本文基于有关单个尘埃粒子散射研究工作基础,采用Mie-Debye模型研究充电平衡态下平面层状尘埃等离子体的电磁散射特性.在带电尘埃颗粒的电磁散射系统中,尘埃颗粒的散射由Mie理论计算,同时将充电电流用矢量波函数展开,求解尘埃颗粒外围Debye云的Debye散射场,以及Mie-Debye相干散射场.对于高层大气中尘埃等离子体环境对电磁波传播的影响分析,主要考虑尘埃等离子体的层状分布对电磁波传播的影响,采用离散纵标法对不同浓度、不同粒径分布的尘埃等离子体电磁散射进行了模拟计算.研究结果表明带电粒子形成Debye云对电磁波的衰减作用非常明显,并明确给出了高层空间环境下带电尘埃颗粒对电磁波的衰减率随尘埃浓度分布、尘埃粒子半径的变化规律.
2 带电尘埃的电磁散射对于高层大气中的尘埃颗粒,一般都视为球形粒子处理.考虑空间等离子体环境中有一个处于充电平衡状态、半径为rd的尘埃颗粒,吸附了一定数量的电子(或离子),在它周围形成半径为λD的屏蔽电子云[5]
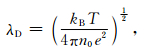
|
(1) |
其中,kB为玻耳兹曼常数,T为背景温度,n0为电子浓度,e为基元电荷.此带电尘埃系统的散射除了中心尘埃粒子的散射外还应该考虑粒子外围Debye云的散射.根据麦克斯韦方程以及流体方程可以给出散射场横向分量ET满足的方程为
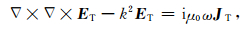
|
(2) |
其中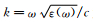
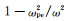
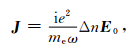
|
(3) |
其中J=JT+JL,JT为充电电流横向分量,JL为充电电流纵向分量.
考虑满足如下方程的第一类并矢格林函数
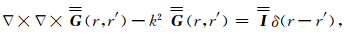
|
(4) |
由于该并矢格林函数在球面边界处满足狄利克雷边界条件,所以将公式(4)代入公式(2)可以得出散射场的横向分量为
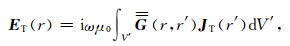
|
(5) |
V′为尘埃粒子体积,将式(5)中的JT用矢量球谐函数M、N、L展开可得散射场的各分量[5].其中Debye场的横向分量为
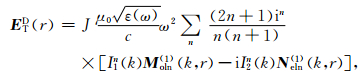
|
(6) |
这里,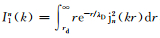
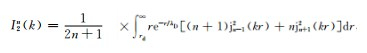
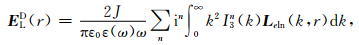
|
(7) |
式中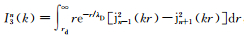
总散射场Etot=ED+EM可看作Debye散射场ED和Mie散射场EM两部分之和,相应的总的散射截面σs_tot由三部分组成σs_tot=σM+σD+σMD,其中由Mie理论得出中心尘埃粒子的散射σM为[5]
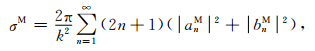
|
(8) |
这里,anM,bnM为采用Mie理论计算球粒子散射截面时的散射系数.
外围Debye云的散射σD为[5]
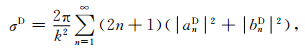
|
(9) |
其中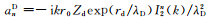
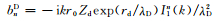
尘埃粒子与外围Debye云的相干截面σMD为[5]
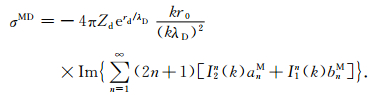
|
(10) |
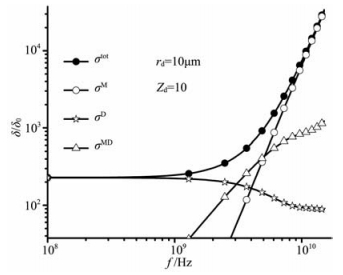
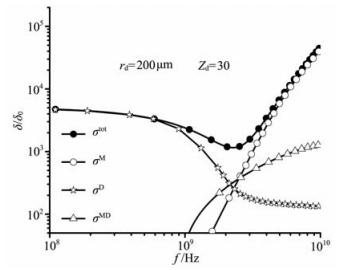
根据上述理论,尘埃粒子的散射场主要受尘埃粒子尺度、复折射率和带电荷数等因素的影响.图 1、图 2分别给出了不同尘埃粒子半径时带电尘埃粒子各散射截面随入射波频率的变化(δ0为汤姆逊截面).其中尘埃粒子的复折射率为1.78+7.78×10-6i (冰晶复折射率),尘埃粒子半径分别为10 μm和200 μm,所带电荷数分别为10和30.从图中可以看出,随着入射电磁波频率的增加,Mie散射截面σM和相干截面σMD迅速增大,而Debye散射截面σD缓慢变小;尘埃粒子的总散射截面在电磁波频率较高时主要来源于Mie散射.另外,通过图 1与图 2的对比还可以发现,随着尘埃粒子半径的增加,带电尘埃粒子的总散射截面是增大的,同时所带电荷数越多,Debye散射截面在较低入射频率时对总散射截面影响越大.
|
图 1 散射截面随入射波频率的变化,rd=10 μm Fig. 1 The scattering section as a function of frequency of the incident wave for rd=10 μm |
|
图 2 散射截面随入射波频率的变化,rd=200 μm Fig. 2 The scattering section as a function of frequency of the incident wave for rd=200 μm |
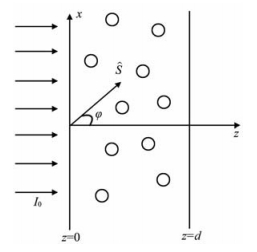
对空间尘埃等离子体的大量观测研究表明,空间尘埃等离子体中电子浓度、尘埃浓度分布呈明显的分层结构[11, 12],所以空间尘埃等离子体环境对电磁波传播的影响,可以看作是平行平面边界随机介质中的波传播问题.考虑在厚度为d的平面平行介质中随机分布着介电性质相同、尺度参数不相同的带电尘埃粒子.强度为I0的平面波垂直入射,选择入射面为xz平面,平板介质的边界平面为z=0和z=d,如图 3所示.
|
图 3 空间尘埃等离子体层电磁散射 Fig. 3 The electromagnetic scattering from layers of dust plasma in the atmosphere |
在研究空间尘埃等离子体中带电尘埃电磁散射特性时,首要的问题是确定尘埃粒子所带电荷数Zd.这里采用轨道受限运动OLM (theorbit-limited motion)方法[13]来计算等离子体中电子和离子对尘埃粒子的充电电流I.电子充电电流Ie和离子充电电流Ii分别为
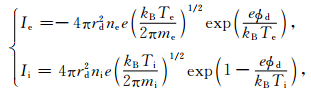
|
(11) |
其中,rd为尘埃粒子半径,me、mi分别为电子质量和离子质量,Te、Ti分别为电子温度和离子温度,ne、ni分别为电子浓度和离子浓度,φd为尘埃粒子表面电势.
根据充电平衡条件Ie+Ii=0,以及电中性条件ni=ne+|Zd|nd,可得
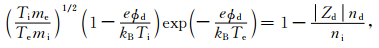
|
(12) |
其中nd为尘埃浓度.又由于尘埃粒子表面电势为
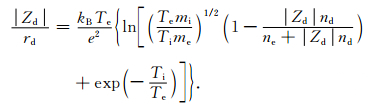
|
(13) |
从式(13)可知,当空间环境中电子浓度、电子温度、离子温度等已知,可以计算得出不同尘埃浓度分布情况下,尘埃粒子所带电荷数Zd与尘埃颗粒半径rd之间的关系.将式(13)代入式(8)~(10)中即可求得一定粒径分布情况下的带电尘埃散射截面.
在分析尘埃等离子体层中波传播问题时,由输运理论可知,当介质内部无源和不计及粒子间相互作用时,总强度I(z,s)=Iri (z,s)+Id (z,s),其中约化入射强度Iri和漫射强度Id分别满足[14]
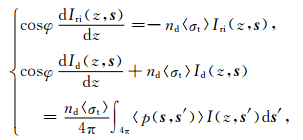
|
(14) |
其中,〈σt〉和〈p(s,s′)〉分别是尺度参数为α=2πr/λ的粒子的平均衰减截面和平均相函数,因为空间中的尘埃等离子体是由半径连续分布的多粒径粒子组成的,显然其散射相函数是多种粒径粒子散射的平均效应,这里平均相函数通常可以表示为s与s′之间夹角θ的函数[14]
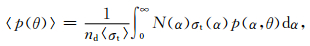
|
(15) |
而平均衰减截面为
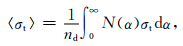
|
(16) |
其中,粒子尺度分布N(α)表示单位粒径间隔单位体积粒子数.衰减截面σt应为吸收截面σa_tot与散射截面σs_tot之和.散射截面由(7)~(9)式可知σs_tot=σM+σD+σMD.而吸收截面σa_tot又分为介电常数虚部ε″引起的吸收截面σam和无旋场引起的吸收截面σad两部分,即
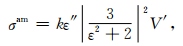
|
(17) |

|
(18) |
根据以上分析,将式(13)代入尘埃粒子衰减截面的计算公式中,求解一定尘埃粒径分布下的平均衰减截面和平均相函数,再将所得结果代入式(14),求解粒子输运方程即可得到不同浓度分布、不同粒径分布下尘埃等离子体层中波传播问题的解.
4 数值计算与讨论尘埃颗粒以空间环境中常见的冰晶颗粒为例来分析带电尘埃颗粒对电磁波传播的影响,其等离子体参数如表 1所示,而冰晶的复介电常数由Ray给出的经验公式确定[15]
|
|
表 1 等离子体参数 Table 1 Plasma parameter |
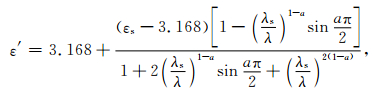
|
(19) |
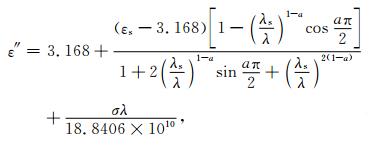
|
(20) |
其中

|
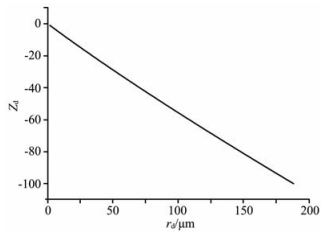
首先根据式(13)分析尘埃粒子所带电荷数与尘埃半径之间的关系.采用表 1中的等离子体参数,计算结果如图 4所示,其结果与P.Bartos[6]所得结论一致,尘埃半径越大,尘埃所带电荷数越多.
|
图 4 尘埃电荷数Zd随尘埃半径rd的变化 Fig. 4 The charge number Zd as a function of radius rd of the dust grains |
根据式(13)确定尘埃粒子所带电荷数Zd,再将rd、Zd等参数代入式(8)~(10)可分别求出带电尘埃粒子的各个散射截面及相函数,如图 5所示.
|
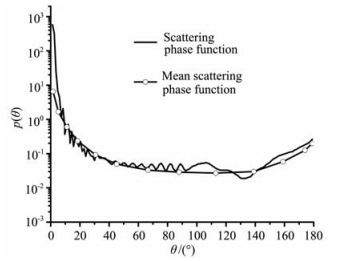
图 5 尘埃粒子的散射相函数 Fig. 5 The scattering phase function of dust grain |
图 5给出尘埃半径r=50 μm带电尘埃颗粒的散射相函数,其中冰晶颗粒的复折射率由式(19),(20)确定.由图 5可以看出未考虑粒径分布时的相函数曲线随散射角增大而逐渐振荡下降,且在大散射角度时又缓慢增大,这与球形粒子散射相函数的变化趋势大致相同.由于空间环境中尘埃颗粒的大小从零点几微米到几百微米不等,图 5中同时给出了考虑粒径分布时的相函数分布.为了准确地计算尘埃粒子对输运过程的影响,这里选用对数正态分布作为尘埃尺度分布函数[16]

|
(21) |
取几何平均偏差σ=1.42,几何平均半径r0=50 μm,将式(21)代入式(15),(16)中计算平均相函数.显然,与未考虑粒径分布时的相函数曲线相比,图 5中考虑粒径分布时随散射角变化的平均相函数曲线较为光滑,这是由于粒径取平均消除了单粒子散射的起伏特征,但总体变化趋势与未考虑粒径分布的相函数是一致的.
采用离散纵标法,由式(14)计算波长λ=200 μm的入射波垂直入射,光学厚度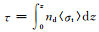
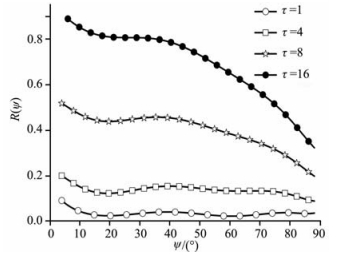
|
图 6 尘埃等离子体层的反射函数 Fig. 6 The reflection function of layers of the dust plasma |
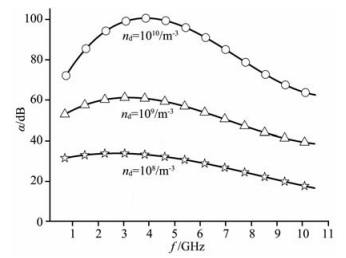
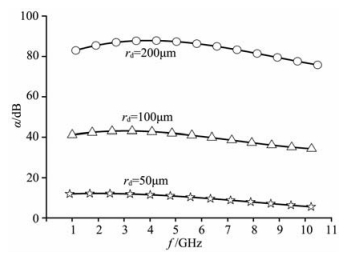
电磁波衰减系数定义为α=|10lg (It/I0)|,其中I0为入射强度,It为透射强度.将式(19)(20)(21)的尘埃模型代入式(15)(16),计算尘埃粒子的平均相函数及平均衰减截面,再采用离散纵标法求解式(14),求出入射电磁波的透射强度.本文采用国际参考电离层IRI2007模型西安地区(108°55′E,34°15′N)的电离层参数以及MSIS模型的中性大气密度和温度剖面,考虑85 km高度处厚度为1 km的尘埃等离子体层.图 7给出电磁波分别在尘埃浓度nd为108,109,1010/m-3的尘埃等离子体层中传播时,衰减系数随入射电磁波频率的变化.图 7中尘埃等离子体层尘埃颗粒平均尺度取为rd=200 μm.图 8给出了电磁波在不同尺度尘埃颗粒rd为50,100,200 μm (平均尺度)形成的尘埃等离子体层中传播时,衰减系数随入射电磁波频率的变化,其中尘埃粒子浓度nd=109/m-3.
|
图 7 尘埃浓度对衰减的影响 Fig. 7 The influence of dust grain density on the attenuation |
|
图 8 尘埃大小对衰减的影响 Fig. 8 The influence of dust grain size on the attenuation |
从图 7中可以看出尘埃等离子体层的衰减随着尘埃颗粒浓度的增加而增加,在较低频段随电磁波频率的增加衰减缓慢加大,而在较高频段随电磁波频率的增加衰减逐渐减小,这与相关实验观测结果[17]是一致的.从图 8中可以看出在背景电离层参数不变的情况下,尘埃粒子尺度越大,对电磁波的衰减也越大.
5 结论根据尘埃等离子体Mie-Debye散射模型,研究平衡态下尘埃等离子体中带电尘埃的电磁波散射特性,计算表明在尘埃尺度满足一定分布的情况下,尘埃颗粒在入射电磁波频率较低时对Debye散射影响较大,而频率较高时电磁散射主要表现为Mie散射.由尘埃粒子的充电方程和静电平衡方程得出的尘埃粒子所带电荷数随尘埃粒子半径变化关系表明,尘埃粒子在不同的粒径分布条件下吸附电荷的能力相差非常大,这将对其电磁散射特性产生重要影响.此外,根据输运理论计算高层大气环境中尘埃等离子体层对电磁波的衰减特性,计算结果表明尘埃等离子体层对于入射电磁波具有高通滤波性质,且电磁波在尘埃等离子体层中的衰减与尘埃粒子浓度、尘埃粒子半径成正比.
| [1] | Klumov B A, Vladimirov S V, Morfill G E. Features of dusty structures in the upper earth's atmosphere. JETP Letters , 2005, 82(10): 632-637. DOI:10.1134/1.2166910 |
| [2] | Grach V S, Demekhov A G, Trakhtengerts V Yu. Dissipative instability of charged aerosol flows in the mesosphere. Radiophysics and Quantum Electronics , 2006, 49(11): 942-957. |
| [3] | Karashtin A N, Shlyugaev Yu V. Angles of arrival of HF mesosphere radar echoes. Geomagnetism and Aeronomy , 2007, 47(2): 260-266. |
| [4] | Bingham R, de Angelis U, Tsytovich V N, et al. Electromagnetic wave scattering in dusty plasmas. Phys. Fluids B:Plasma Physics , 1991, 3(7): 811-817. |
| [5] | Guerra R, Medonca J T. Mie and Debye scattering in dusty plasmas. Phys. Rev. E , 2000, 62(1): 1190-1201. DOI:10.1103/PhysRevE.62.1190 |
| [6] | Bartos P, Blazek J, Jelinek P, et al. Hybrid computer simulations:electrical charging of dust particles in low-temperature plasma. The European Physical Journal D , 2009, 29(5): 1140-1145. |
| [7] | 李芳, HavnesO. 电磁波被尘埃等离子体散射的功率谱. 电子科学学刊 , 1999, 21(5): 679–686. Li F, Havnes O. Scatter spectrum of radio waves by a dusty plasma. Journal of Electronics (in Chinese) , 1999, 21(5): 679-686. |
| [8] | 李芳, 李廉林, 隋强. 等离子体中尘埃粒子对电磁波的吸收效应. 中国科学E辑 , 2004, 34(7): 832–840. Li F, Li L L, Sui Q. Absorption of electromagnetic waves by the dust particles in a plasma. Science in China (Series E:Engineering & Materials Science) (in Chinese) , 2004, 34(7): 832-840. |
| [9] | 石雁祥, 葛德彪, 吴健. 尘埃等离子体微波衰减常数的理论分析. 地球物理学报 , 2007, 50(4): 1005–1011. Shi Y X, Ge D B, Wu J. Theoretical analysis of micro wave attenuation constant of weakly ionized dusty plasma. Chinese J. Geophys. (in Chinese) , 2007, 50(4): 1005-1011. DOI:10.1002/cjg2.v50.4 |
| [10] | 石雁祥, 葛德彪, 吴健. 尘埃粒子充放电过程对尘埃等离子体电导率的影响. 物理学报 , 2006, 55(10): 3290–3297. Shi Y X, Ge D B, Wu J. Influence of charge and discharge processes of dust particles on the dust plasma conductivity. Acta Physica Sinica (in Chinese) , 2006, 55(10): 3290-3297. |
| [11] | Havnes O, Trøim J, Blix T, et al. First detection of charged dust particles in the Earth's mesosphere. J. Geophys. Res. , 1996, 101(A5): 10839-10847. DOI:10.1029/96JA00003 |
| [12] | Chilson P B, Yu T Y, Palmer R D. Aspect sensitivity measurements of polar mesosphere summer echoes using coherent radar imaging. Annales Geophysicae , 2002, 20(2): 213-223. DOI:10.5194/angeo-20-213-2002 |
| [13] | Shukla P K, Mamun A A. Introduction to Dusty Plasma Physics. Institute of Physics Publishing Bristol and Philadelphia, 2001 |
| [14] | Ishimaru A. Wave Propagation and Scattering in Random Media. New York: Academic Press, 1978 . |
| [15] | Ray P S. Broadband complex refractive indices of ice and water. Applied Optics , 1972, 11(8): 1836-1844. DOI:10.1364/AO.11.001836 |
| [16] | Savigny C V, Petelina S V, Karlsson B. Vertical variation of NLC particle sizes retrieved from ODIN/OSIRIS limb scattering observations. Geophys. Res. Lett. , 2005, 32(7): 7806-7818. |
| [17] | Baghdady E J, Ely O P. Effects of exhaust plasmas upon signal transmission to and from rocket powered vehicles. Proceedings of the IEEE , 1966, 54(9): 1134-1146. DOI:10.1109/PROC.1966.5059 |
 2010, Vol. 53
2010, Vol. 53


