核磁共振广泛应用于生物医学、无损检测、石油勘探等领域.在石油勘探中,由共振所产生的自旋回波串能观测到常规测井仪器难以提供的岩石孔隙流体体积、流体特性、含流体孔隙尺寸等重要信息,提供孔隙度、流体类型、渗透率等重要参数,已成为一种应用广泛的测井方法[1].但采集到的回波信号通常比较微弱,一般只有几十纳伏(nV),容易受到来自电子器件、电磁场和外部环境的干扰.如何有效抑制回波信号中的噪声、增强数据信噪比一直是核磁共振技术研究的关键问题之一.
Cobas等[2]讨论了一种基于数据压缩的方式对核磁共振回波信号去噪的方法,采用较高压缩比时能较好地重构多维NMR谱;郑传行等[3]讨论了基于小波变换的UDWT(Undecimated wavelet transform)方法,在保持回波信号峰值的同时进行去噪,但是在数据信噪比较低的时候噪声不能得到较好的压制.本文讨论了一种基于小波变换的多分辨率Stein无偏风险估计(Stein Unbiased Risk Evaluation,SURE)算法[4],通过尺度因子和分解层次的相关系数图版确定最优化参数,根据噪声分量在不同分解层次的差异,在不同分解尺度下采用自适应、软取阈值的方式有效消除核磁共振回波信号中的噪声,提高数据的信噪比,为储层解释和评价提供更为准确的信息.
2 小波变换原理近几年来,小波变换因其实用、简单、便捷、去噪效果明显等优点广泛应用于数据压缩、图像处理、地震勘探资料预处理、雷达通信、信号降噪等领域.
小波变换即把基本小波函数(母小波函数)作位移后,在不同的尺度a下与待分析信号x(t)作内积[4, 5].主要分为连续小波变换CWT(Continuous Wavelet Transform)和离散小波变换DWT(Discrete Wavelet Transform).针对信号的不同特点,常用的小波去噪方法有:Mallat提出的模极大值重构去噪[5, 6]、Xu等提出的空域相关法去噪[7]、Donoho提出的阈值去噪[8~12]等.阈值去噪法直接在各尺度上对小波系数进行阈值处理,其关键是确定阈值,噪声能得到很好的抑制,且信号的特征突变点能得到很好的保留.Donoho曾提出通用阈值选取公式[8],在任何尺度和分解层次下选用统一的阈值:

|
(1) |
潘泉等[13]对阈值选取公式做了一些改进:
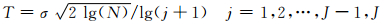
|
(2) |
但在回波信号的去噪中并不理想.式中,σ为噪声方差,N为数据采样点数,J为小波分解层次.本文采用多分辨率自适应SURE算法,针对多尺度、不同分解层次下的回波信号选取不同的阈值去噪,能很好地消除信号中的白噪声.
3 多分辨率SURE算法多分辨率SURE算法[9]对信号采用多尺度、自适应、软取阈值的分析方法,在不同的分解层次上选取不同的阈值对小波系数进行滤波处理.
设接收到的信号为X(t)=f(t)+w(t),f(t)为信号,w(t)为噪声.设B为规范正交基,B={gm},0≤m<N,gm为滤波器系数,m为分解层次下的小波系数个数.带噪信号X(t)在规范正交基B下分解为高频小波系数WB[m]和低频小波系数fB[m],且满足:
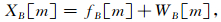
|
(3) |
式中,XB[m]为X(t)的小波系数.带噪信号X(t)通过一个决策算子D来估计原信号f(t),决策算子D是正交基B下的投影,通过优化D以便最小化期望风险,所得的估计子为:
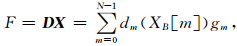
|
(4) |
其中,dm为阈值函数.对于不同的取阈值方式,有:
(1)硬取阈值:

|
(5) |
(2)软取阈值:
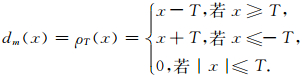
|
(6) |
在小波基下,阈值估计子可改写为:
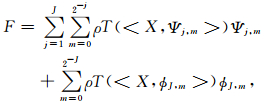
|
(7) |
式中,J为分解层次,Ψ为小波,ϕ为尺度函数,ρT(x)为硬(或软)取阈值函数,〈X,Ψj,m〉为小波分解系数.由式(5)可知,对于阈值估计方法,估计风险的大小与阈值密切相关.为了提高信号的信噪比,可以通过最小化风险估计,计算自适应于数据或小波分解系数的阈值.
设r(f,T)为阈值T时的估计子风险,由带噪数据X(t)计算而得,T可以通过求极小化的r(f,T)而被优化.Donoho和Johnstone认为可用|XB[m]|2 -σ2来估计|fB[m]|2,所得的估计子为[9]:
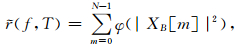
|
(8) |
其中:
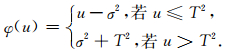
|
(9) |
Donoho和Mallat在文献[10]中已证明:通过忽略f的影响,可由小波系数的中位Mx来估计噪声的方差:
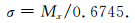
|
(10) |
此时,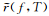
为了寻找最小的SURE估计子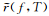

|
(11) |
则,式(6)可以改写为:
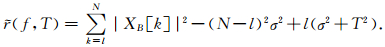
|
(12) |
Donoho已在文献[10]中证明,当取T=XB[l]时,可以得到最小化的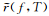
将阈值选取自适应于尺度2j,可形成多分辨率SURE阈值算法:在大尺度2j,阈值Tj应该较小,以避免将太多的大幅值信号系数置为零,这样会增加风险;在小尺度2j,阈值应该较大,能准确将信号与噪声的小波系数分辨出来,达到去噪的目的.
根据核磁共振回波信号的特点,本文分别选用Symlets小波和Daubechies小波作为基函数,通过尺度因子、消失矩、相关系数三者的组合图版,选取最大相关系数下的尺度因子和消失矩,并对信号进行分解[14],运用SURE算法在不同的分解层次下对信号进行去噪处理.
4 算法仿真本文通过对比去噪前后回波信号的反演结果来检验SURE算法的有效性.实现步骤为:
(1)构造一个T2谱双峰模型,通过正演计算得到回波串信号;
(2)给回波串信号增加噪声,降低信噪比;
(3)利用多分辨率SURE算法对带噪信号进行去噪处理,得到新信号;
(4)采用SVD反演方法[15]对新信号进行反演,对比去噪前后T2谱和信噪比的变化;
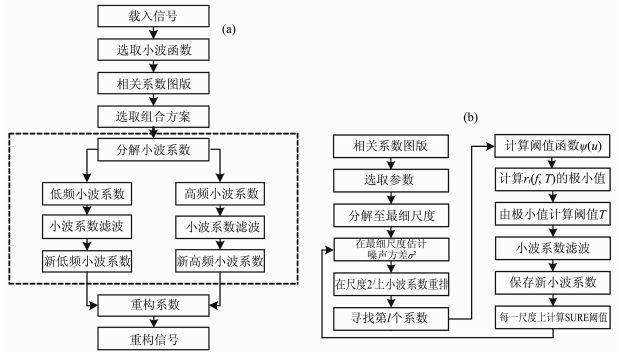
整个去噪处理流程如图 1所示.图 1a为小波变换去噪的处理流程,虚线方框内为SURE算法,具体实现流程如图 1b所示.
|
图 1 小波变换处理流程 (a)去噪流程;(b) SURE算法流程. Fig. 1 Wavelet processing flow chart (a) De-noising flowchart; (b) SURE algorithm flowchart. |
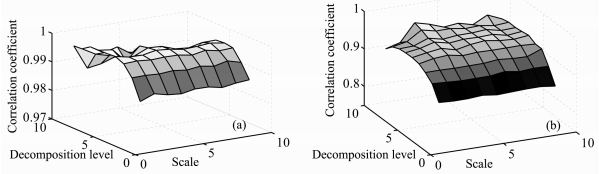
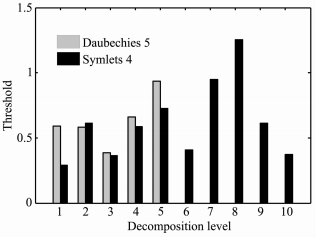
根据低场核磁共振回波信号呈多指数衰减的特点,选用具有紧支撑性和双正交性的Daubechies小波和Symlets小波,通过尺度因子、消失矩、相关系数三者的组合图版,选取具有最大相关系数的尺度因子和消失矩对信号进行分解.如图 2所示,当尺度因子为5,消失矩为5时,Daubechies小波具有最高的相关系数(相关系数为0.995);Symlets小波在尺度因子为4,消失矩为10的时候具有最大的相关系数(0.951).图 3为Symlets4小波和Daubechies5小波在不同分解层次依据式(8)和式(12)计算出的SURE算法阈值.
|
图 2 Daubeches小波(a)、Symlets小波(b)的相关系数图版.相关系数、消失矩、尺度因子均为无量纲(下同) Fig. 2 Correlation coefficient plate for Daubechies (a) and Symlets (b). All units are dimensionless |
|
图 3 Daubechies 5小波和Symlets 4小波在不同分解层次的阈值 Fig. 3 Thresholds in different decomposition level for Daubechies 5 and Symlets 4 |
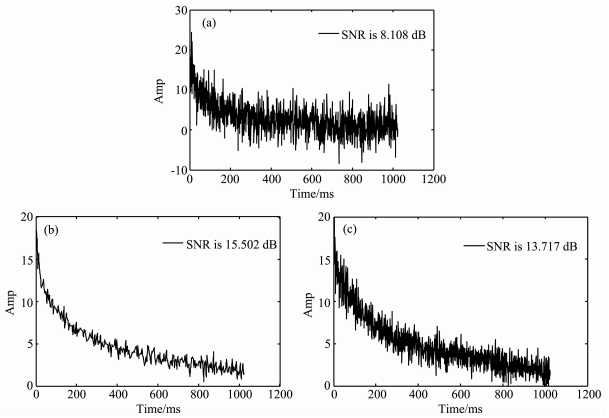
图 4为核磁共振回波模型去噪前后的对比.由图 4a中可知,回波信号具有较大的噪声分量,信噪比仅为8.108dB.采用多分辨率SURE算法对带噪信号去噪处理后,噪声分量得到了很好的压制,信噪比分别提高到了15.502dB和13.717dB,如图 4b和图 4c所示.图 4b为选用Daubechies5小波,5层分解的去噪结果;图 4c为选用Symlets4小波,10层分解去噪结果.
|
图 4 SURE算法在不同小波基下的去噪结果 Amp为相对信号幅度,无量纲;Trnie为回波采集时间(下同):(a)带噪回波串,SNR为8.108 dB; (b) Daubeches 5小波去噪结果,SNR为15.502 dB; (c) Symlets 4小波去噪结果,SNR为13.717 dB. Fig. 4 De-noising results based on different mother wavelet using SURE algorithm Amp is the relative amplitude. Time is acquisition time. (a) Noisy echo train, SNR is 8. 108 dB; (b) De-noising result of Daubechies 5, SNR is 15. 502 dB; (c) De-noising result of Symlets 4, SNR is 13. 717 dB. |
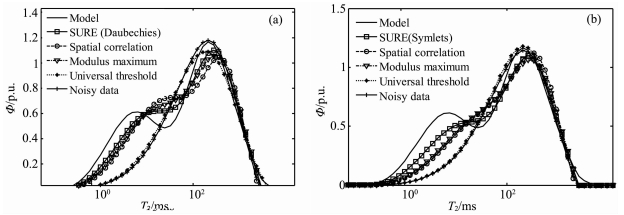
为了检验本文算法的优越性,对比分析了模极大值重构法[6]、空域相关法[7]、通用软阈值法[8]与SURE算法去噪后的回波信号SVD反演结果,如图 5所示.图 5a与5b分别选用Daubechies 5小波和Symlets 4小波作为母小波,由图可知:增加噪声后的回波信号反演为单峰特征,其T2谱与模型有较大的差异,丢失了微孔组分的信息;由于核磁共振回波串信号的噪声系数在不同的分解层次上具有不同特性,通用软阈值法在各个分解层次上选取统一的阈值,去噪效果不明显,信噪比变化不大,T2谱不能体现微孔组分;由于小尺度下的小波系数受噪声影响较大,模极大值重构去噪方法在小尺度下产生的伪极值点易被认为是真实信号的小波系数;空域相关法适合于较高信噪比数据,对于低场核磁共振低信噪比数据去噪,容易产生间断、不连续点.而且,如果不同尺度下的小波系数位置发生偏移,则不能反映小波系数的真实相关性.但是,由于信噪比的提高,模极大值重构法和空域相关法的T2谱已逐渐体现微孔组分;采用多分辨率SURE算法,在不同尺度、不同分解层次上选取不同的阈值,克服了以上去噪方法的缺点,去噪后信噪比得到了较大提高,反演结果已能分辨微孔组分,T2谱趋向双峰,更为接近原模型.
|
图 5 不同算法去噪后的T2谱对比 Φ为刻度后的孔隙度,T2为横向弛豫时间.(a)Daubechies 5小波各种算法对比;(b)Symlets 4小波各种算法对比.“-”,构造的模型;“□”,SURE方法;“o”,空域相关法;“ Δ”,模极大值重构法;“*”,通用软阈值法;“+”,带噪回波信号. Fig. 5 Comparison of T2 spectrum using various de-noising algorithm. Φ is porosity after calibration, T2 represents transverse relaxation.(a) Daubechies 5;(b) Symlets 4 |
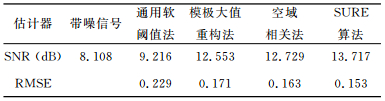
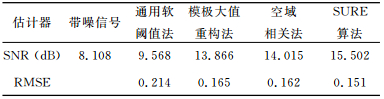
本文以均方根误差(RMSE)和信噪比(SNR)为比较参量,对比分析了上述几种小波去噪方法.通常情况下,有较好的SNR和较低的RMSE的算法具有更好的去噪性能.表 1和表 2的数据证明:在处理低场核磁共振低信噪比数据时,SURE算法具有最好的去噪性能,模极大值重构法和空域相关法次之,Donoho提出的通用软阈值法效果最差.
|
|
表 1 各种算法去噪效果对比(Symlets 4) Table 1 Comparison of different de-noising algorithm (Symlets 4) |
|
|
表 2 各种算法去噪效果对比(Daubechies 5) Table 2 Comparison of different d--noising algorithm (Daubechies 5) |
为了验证算法的有效性,使用Oxford DRX核磁共振数字化谱仪对10块四川普光气田A井的碳酸盐岩岩芯进行了孔隙度测量.称重孔隙度测量采用岩芯常规分析方法(烘箱恒温90℃,连续24h烘干,然后水饱和48h).核磁共振实验采用CPMG脉冲序列,90°脉冲持续时间9μs,180°脉冲持续时间18μs,采样频率100kHz,回波个数8192,回波间隔600μs,累加4次,实验结果及SURE算法去噪后的计算结果如表 3所示.
|
|
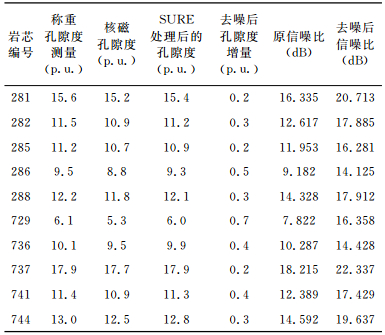
表 3 普光气田犃井岩芯孔隙度测量与算法处理结果比较 Table 3 Comparisons of core porosity measurements and SURE processing for well A in Puguang gas field |
由表 3可知,所测岩芯最大孔隙度为岩芯737,称重孔隙度测量与核磁孔隙度测量误差为0.2p.u.(p.u.,孔隙度单位,用100%饱和岩芯后剩余的水进行刻度);孔隙度最小为岩芯729,称重孔隙度测量与核磁孔隙度测量误差为0.7p.u.,称重孔隙度较核磁共振测量结果偏大,主要由于存在核磁共振岩芯分析仪内部电子器件产生的噪声对核磁共振测量的影响.运用本文算法对数据做去噪处理后,削弱了噪声影响,减小了两种测量方法的误差.而且,在相同的实验条件下,岩芯孔隙度越大,孔隙中含有的1H质子数目越多,核磁共振回波信号幅度相对较大,与低孔隙度测量数据相比信噪比更高,测量的孔隙度与称重孔隙度测量更接近;具有低孔隙度的岩芯由于核磁共振回波信号幅度相对较小,受到噪声污染后信噪比更低.低信噪比数据在反演时,为了压制噪声分量对反演结果的影响,选取的奇异值截止值较大,奇异值保留个数减少,反演后的孔隙度相对称重孔隙度误差较大;当数据信噪比较大时,为了保留更多回波信息,奇异值截止值的选取较小,奇异值保留个数较多,反演后的孔隙度更接近于称重孔隙度.
SURE算法去噪前后孔隙度的增量变化还与小尺度上选取的小波系数阈值有关.由于噪声能量主要集中在小尺度,当数据信噪比较低时,小尺度小波系数的阈值选取较大,噪声得以有效抑制,反演时保留了更多的奇异值,从而使得去噪前后孔隙度增量较大;当数据信噪比较高时,为了保留更多的信号,小尺度上选取的阈值较小,小波系数保留较多,反演前后孔隙度的增量较小,从而体现了SURE算法的自适应特性.
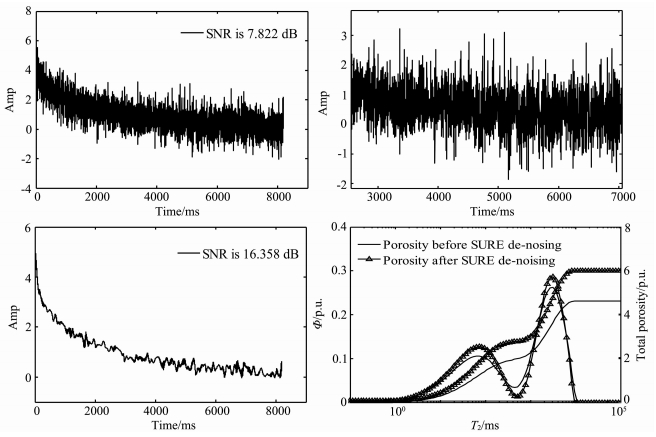
以孔隙度最小的729号岩芯为例,运用本文讨论的SURE算法对测量数据做去噪处理,比较回波信号的信噪比及反演后岩芯孔隙度变化.采集到的回波信号如图 6a所示;图 6b为采集到的回波信号放大,有用信号被淹没在大量的噪声中,数据的信噪比较低.
|
图 6 SURE算法去噪前后的回波信号及T2谱与总孔隙度 (a)带噪回波串;(b)放大后带噪信号;(c)运用SURE算法去噪后的信号;(d)去噪前后数据的T2谱与总孔隙度. Fig. 6 De-noising results of echo train, T2 spectrum and total porosity (a) Noisy echo train; (b) Noisy data (close-up); (c) De-noising result using SURE algorithm in Daubechies 4; (d) Comparison of T2 spectrum and total porosity. |
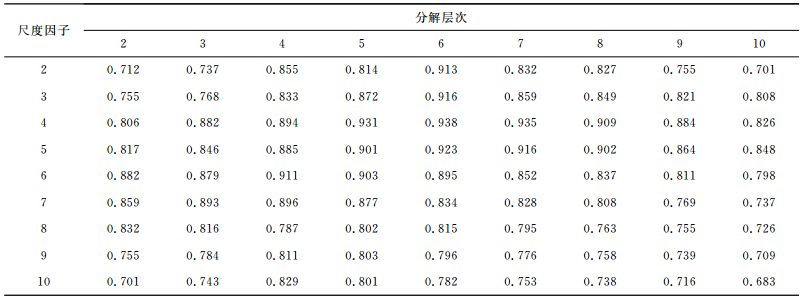
选取Daubechies小波作为母小波,尺度因子、消失矩与原信号平均去噪效果的相关系数如表 4所示.对应最高相关系数(0.938)的尺度因子和消失矩分别为4和6,选用Daubechies4小波对带噪信号6层分解.使用本文讨论的SURE算法对带噪信号去噪,由式(8)和式(12)计算的各层阈值如表 5所示.去噪后的回波信号如图 6c所示,可见原信号中的噪声分量得到了很好的压制.图 6d为带噪信号和去噪信号通过SVD反演后的T2谱,去噪前原数据信噪比为7.822dB,去噪后信噪比为16.358dB;利用去噪前的回波信号计算的总孔隙度为5.3p.u.,而去噪后计算的岩芯总孔隙度为6.0p.u.,更接近称重孔隙度(6.1p.u.).可见,本文所用算法有效地提高了回波信号的信噪比,反演时保留了更多的奇异值,反演结果更接近于称重方法得到的岩芯孔隙度.
|
|
表 4 尺度因子和分解层次的相关系数表 Table 4 Correlation coefficient of scale and decomposition level |
|
|
表 5 Daubechies 4小波不同分解层次下的SURE算法阈值 Table 5 SURE thresholds of Daubechies 4 in different decomposition level |
核磁共振产生的回波信号易受到噪声干扰.采用基于小波变换的多分辨率SURE算法,通过寻找小波基下最优尺度因子与分解层次,根据噪声分量的变化,自适应选取阈值.与传统的小波去噪方法相比,能更好地压制噪声,降低最小化估计的风险.实验表明,利用SURE算法去噪后的回波数据,能获得更高的信噪比,更能准确地反映岩芯孔隙度信息.在实际测井应用中,核磁共振测井数据信噪比受到地层孔隙度大小、探测区域样品体积、钻井液矿化度、测井仪运动速度等多方面的影响,噪声成分较实验室岩芯分析要复杂的多.因此,在后续研究中,将运用本文算法对核磁共振测井资料的去噪处理做进一步讨论.
| [1] | Coates G R, Xiao L Z, Prammer M G. NMR logging:principles and applications. Texas: Gulf Professional Publishing, 2000 . |
| [2] | Cobas J, Tahoces P G, Pastor M M, et al. Wavelet-based ultra-high compression of multidimensional NMR data sets. Journal of Magnetic Resonance , 2004, 168(2): 288-295. DOI:10.1016/j.jmr.2004.03.016 |
| [3] | Zheng C X, Zhang Y M. Low-field pulsed NMR signal de-noising based on wavelet transform. Signal Processing and Communications Applications, SIU, 2007, IEEE 15th.1~4 http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4298696 |
| [4] | 杨福生. 小波变换的工程分析与应用. 北京: 机械工业出版社, 1999 . Yang F S. Wavelet Analysis and Its Engineering Applications (in Chinese). Beijing: China Machine Press, 1999 . |
| [5] | Mallat S. A wavelet Tour of Signal Pprocessing. Burlington: Elsevier Science, 2009 . |
| [6] | Mallat S. A theory for multiresolution signal decomposition:the wavelet representation. IEEE TPAMI , 1989, 11(7): 674-693. DOI:10.1109/34.192463 |
| [7] | Xu Y S, Weaver J B, Healy D M, et al. Wavelet transform domain filters:a spatially selective noise filtration technique. IEEE Transactions on Image Processing , 1994, 3(6): 747-758. DOI:10.1109/83.336245 |
| [8] | Donoho D L, Johnstone I M. Ideal spatial adaptation via wavelet shrinkage. Biometrika , 1994, 81(12): 425-455. |
| [9] | Donoho D L, Johnstone I M. Adapting to unknown smoothness via wavelet shrinkage. J. American Statist. Assoc. , 1995, 90: 1200-1224. DOI:10.1080/01621459.1995.10476626 |
| [10] | Donoho D L, Johnstone I M. Wavelet shrinkage:asymptopia? J. of Royal Stat. Soc.B. , 1995, 57(2): 301-369. |
| [11] | Donoho D L, Mallat S, Sachs R V. Estimating covariances of locally stationary processes:consistence of best basis methods. In Proc. of Time-Freq. and Time-Scale Symp., 1996. 337~340 http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=547482 |
| [12] | Song G X, Zhao R Z. Three novel models of threshold estimator for wavelet coefficients. 2nd International Conference on Wavelet Analysis and Its Applications, 2001.145~150 http://link.springer.com/chapter/10.1007/3-540-45333-4_19 |
| [13] | 潘泉, 张磊, 孟晋丽, 等. 小波滤波方法及应用. 北京: 清华大学出版社, 2005 . Pan Q, Zhang L, Meng J L, et al. Wavelet Filtering Method and Its Applications (in Chinese). Beijing: Tsinghua University Press, 2005 . |
| [14] | 王希武, 董光波, 谢桂海, 等. 基于小波变换的核磁共振FID信号的去噪方法研究. 核电子学与探测技术 , 2008, 28(2): 365–370. Wang X W, Dong G B, Xie G H, et al. A new de-noising method of NMR FID signals based on wavelet transform. Nuclear Electronics & Detection Technology (in Chinese) , 2008, 28(2): 365-370. |
| [15] | Dunn K J, Bergman D J, Latorraca G A. Nuclear Magnetic Resonance:Petrophysical and Logging Applications. Pergamon: Elsevier Science, 2002 . |
 2010, Vol. 53
2010, Vol. 53