2. 吉林大学通信工程学院, 长春 130012
2. College of Communication Engineering, Jilin University, Changchun 130012, China
在油井工程中,固井质量评价是保证油气井稳定生产的重要环节.声波测井是应用最普遍也是最有效的固井质量检测技术.声波测井的解释方法基于套管井井孔声学理论.轴对称套管井中的声波传播理论已被广泛研究[1~6],并被有效地应用到生产实际中广泛使用的声波-变密度测井(CBL-VDL)解释.但声波-变密度测井轴对称发射-接收,只能给出井周水泥胶结情况的平均结果,不能指示周向水泥缺失分布.为克服这一不足,20世纪90年代以来又发展出新一代有周向方位识别功能的扇区水泥胶结测井装置(SBT),典型的仪器有两种:一种是6极板贴井壁测量的补偿声波水泥胶结测井,一种是柱状声系8扇区沿井8发8收的声波水泥胶结测井.他们都是采用非轴对称声系探测井周围局部水泥胶结情况,但声系结构差别很大.针对这类测井方法开展非轴对称套管井声场的理论研究,尤其是对同时有水泥局部缺失情况下瞬态全波声场的模拟计算与分析,将有助于改进水泥环周向分布的解释方法和提高解释精度,这正是油田开发所需要的.然而针对SBT探测非轴对称套管井水泥局部胶结问题开展的理论工作尚比较少.文献[7]和[8]都是针对贴井壁极板型SBT测井进行数值研究,且采用的是简化模型,考虑了声源偏心时的非轴对称性,却都没有顾及套管井的柱状多层结构和水泥局部缺失的实际复杂性.文献[9]采用2.5维有限差分算法计算了带扇形窜槽的套管井中声场,只是其声源为主频10kHz的单极点源,不能反应SBT测井主频100kHz柱状声系扇形声源激发的套管井内声场规律.而对8扇区的扇区水泥胶结测井(SBT)的理论与数值模拟问题,只有文献[10](第一作者博士论文)有所涉及.
本文主要针对8扇区的SBT测井,数值地计算与研究水泥环任意方位有不同大小水泥局部缺失的非轴对称套管井中SBT测井波形.我们采用已广泛应用于研究井孔声学问题的时域应力-速度有限差分(SVFD)方法[11~17].用有限差分模拟无限大介质中的波传播问题时,要用到吸收边界条件,本文采用了非裂化的完全匹配层吸收边界条件(NPML)[18].由于SBT测井的主频较高(100kHz),有限差分模拟需要很大的内存和计算时间,普通计算机很难完成.为克服这一困难,我们引入可在计算机集群上运行的基于信息传递接口(MPI)的并行算法[19~21].
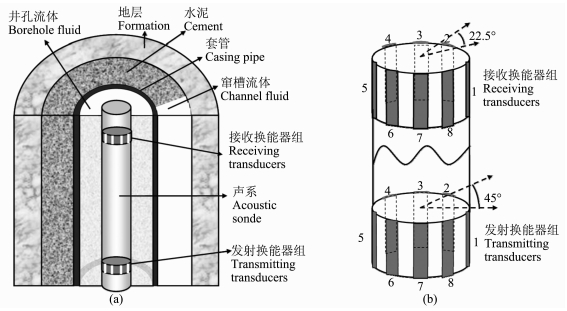
2 并行有限差分方法 2.1 测井模型SBT测井模型见图 1a.从内向外依次为测井仪、井孔流体、套管、水泥环和半无限大地层.水泥环中的扇区缺失部分由窜槽流体填充,在本文中窜槽流体和井孔流体参数相同.测井仪声系包含8个发射换能器和8个接收换能器,如图 1b所示.接收和发射换能器组中心的距离为0.6096 m(2ft).发射(接收)换能器等间距分布在声系柱面圆周上,相邻的两换能器中心线间夹角为45°,每个换能器周向边界对其中心线的张角为22.5°.测井仪用局部表面径向振动的刚性柱来模拟.8扇区测井仪的8对换能器成对轮流发射接收,在每个深度点记录8条波形.
|
图 1 扇区水泥胶结测井模型示意图(a)和测井仪声系示意图(b) Fig. 1 Schematic diagrams of the SBT logging model (a) and acoustic sonde of SBT tool (b) |
图 1a所示模型为柱状多层结构,我们采用柱坐标系,z轴与井轴重合.柱坐标系下的波动方程、NPML中修正的方程以及NPML有限差分实现等内容在文献[18]中已有论述,为了方便读者以及下文的表述,这里还是简要给出.对均匀各向同性介质,波场满足以下方程:
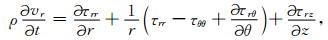
|
(1) |
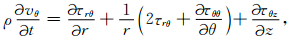
|
(2) |
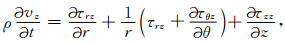
|
(3) |
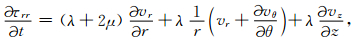
|
(4) |
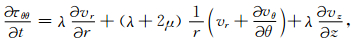
|
(5) |
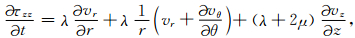
|
(6) |
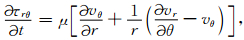
|
(7) |

|
(8) |
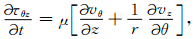
|
(9) |
其中vα为速度分量,ταβ为应力分量,α,β=r,θ,z;ρ,λ和μ分别为密度和拉梅系数.
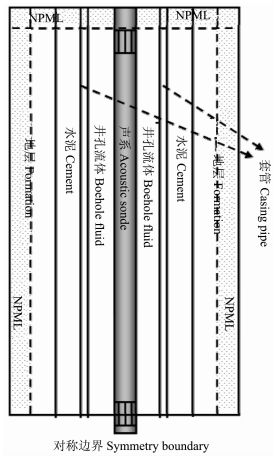
为消除有限大模型外边界的人为反射波,NPML被用来包围计算区域.我们令发射换能器中心所在平面为对称边界,这样下边界就不需要NPML层,从而提高计算效率.如图 2所示,NPML只出现在径向最外层以及接收换能器以上的区域.
|
图 2 对称边界与NPML吸收边界纵剖面示意图,阴影区为NPML区域 Fig. 2 Schematic diagramof longitudinal section of symmetry boundary and NPML absorbing boundary. The shaded regions are NPMLs |
在NPML区域,波动方程(1)~(9)通过把空间坐标拓展到复变量域引入衰减.下面以方程(1)为例,给出NPML区域修正的波动方程的推导过程.在e-iωt假设下,方程(1)在频率域可写为
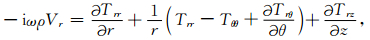
|
(10) |
其中Vr和Tαβ分别为vr和ταβ的Fourier频谱.在NPML区域,空间坐标q(q=r,z)替换为复坐标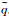
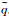

|
(11) |
其中
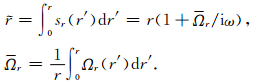
|
将方程(11)进行Fourier逆变换到时域可得
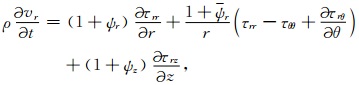
|
(12) |
其中ψq=-Ωqe-Ωqt*,ψr=-Ωre-Ωrt*,*为卷积算符.当Ωq=0,Ωr=0时,方程(12)自动退化为内部区域的原始波动方程(1).根据参考文献[18],我们选取Ωq(q)=Ωq0(aη+bη2),其中Ωq0=-(Vmaxlnα)/L,η=q/L,L为NPML区域的厚度,Vmax为NPML区域中介质的最大体波速度,a=0.25,b=0.75,α=10-6.为保证吸收效果,本文计算中取L大于等于介质中的最小半波长.
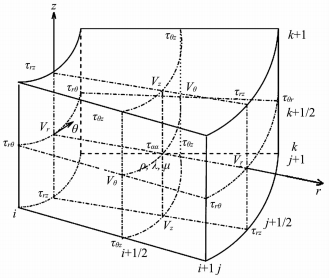
2.3 方程离散化速度和应力场,密度和拉梅系数被离散化到交错网格上,如图 3(修改自文献[16])所示.径向网格从测井仪半径处开始,这样可以避免井轴上的奇异点,简化程序.空间和时间网格步长分别为Δr,Δθ,Δz和Δt.对时间的微分采用二阶中心差分来近似,微分方程(12)可写为
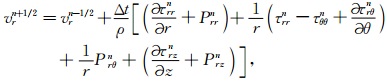
|
(13) |
|
图 3 柱坐标系下有限差分交错网格(修改自文献[16]) Fig. 3 The FDTD staggered grid in cylindrical coordinates (modified from reference [16]) |
其中n是时间步序号,r=iΔr,上式省略了空间网格序号(i,j+1/2,k+1/2),其中
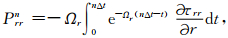
|
(14) |
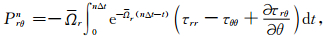
|
(15) |
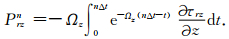
|
(16) |
为了使(14)~(16)式具有方便时间迭代的形式,积分由求和来近似,例如
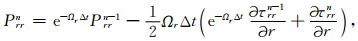
|
(17) |
以上各式中,空间微分也用二阶中心差分近似,例如
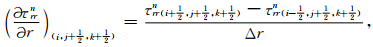
|
(18) |
应力场和密度选取(i,j+1/2,k+1/2)处的算术平均值,例如
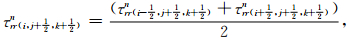
|
(19) |
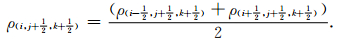
|
(20) |
应该强调的是,当将方程(7)~(9)差分化时,拉梅系数μ选取了该点的调和平均值,以方程(7)为例
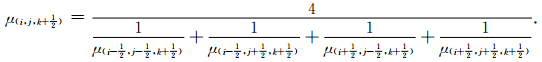
|
(21) |
当(21)式等号右侧的4个值中任意一个或多个为零时,视为其倒数无穷大,则该式分母无穷大,取零值.(21)式可以使得流-固界面上剪切应力为零,从而提高了数值计算的稳定性和精度.
测井仪器用局部表面径向振动的刚性柱来模拟,仪器和套管内流体的边界为刚性边界,声波不在仪器中传播.由于声源位于刚性边界上,无法使用传统的声源加载方式[22],我们通过定义发射扇区的径向粒子速度模拟发射换能器(设r0=i0Δr为刚性柱半径)
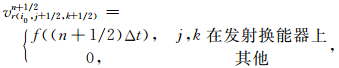
|
(22) |
声源脉冲函数为瑞克子波f(t)=4α2t2e-αtsinω0t,其中ω0=2πf0,f0为中心频率,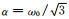
空间步长按照下式定义:
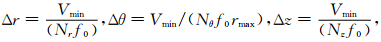
|
(23) |
时间步长为[15]
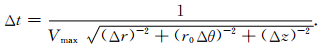
|
(24) |
为保证计算精度,本文取Nr,Nθ,Nz大于等于7. Vmax和Vmin分别为模型中介质的最大和最小体波速度,rmax为模型外边界的半径.
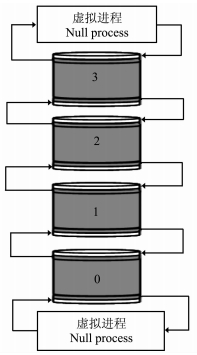
2.4 基于MPI的并行程序设计我们采用网格并行的方式,将整个计算模型分为多个子区域,每个进程计算一个子区域,这样只有子区域边界的场需要数据交换,数据通信量较小,适合在计算机集群这种分布式内存的并行计算机上运行.考虑到计算速度和编程的方便,我们沿井轴方向分割网格.图 4是以调用4个进程为例,网格划分和进程间通信的示意图.整个模型沿轴向分为4段,即4个子区域,0,1,2,3为子区域所在进程的标识.每个子区域中灰色的部分为计算区域,在计算区域边界上的数据在每一时间步都要发送到相邻的进程,白色的区域是用来接收相邻进程发送的数据的缓冲区.进程间通信用箭头表示,箭头端指向接收进程,另一端为发送进程.从二阶中心差分格式(18)式以及交错网格图 3可知,边界上的vr,vθ,τzz要被发送到上面的进程,而vz,τrz,τθz要被发送到下面的进程.进程1和2都需要和两边相邻的进程通信,而进程0只需要向上通信,进程3只需要向下通信.为了编程方便,我们引入虚拟进程[19].虚拟进程是虚无的进程,当真实的进程调用发送或接收命令时,来充当通信的目标进程或源进程.该调用会立即返回,不读写任何缓冲区.引入虚拟进程可以简化程序结构.
|
图 4 网格划分和进程间相互通信示意图 Fig. 4 Schematic diagram of grid partition and communications between processes |
在有限差分计算中,每个时间步都需要进行数据通信.我们采用重复非阻塞通信(RNC)来重叠计算和通信[19].在每一时间步,先计算边界上需要通信的数据,然后调用RNC,再计算内部区域的数据,计算结束后完成RNC.重复非阻塞通信的使用使得通信不需要等待,而且基本不占用计算时间,极大地提高了计算速度.
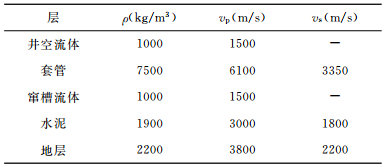
3 方法验证与模拟结果 3.1 并行算法的验证为验证算法的正确性,我们将图 1中模型退化为轴对称情况,将用并行有限差分方法模拟的波形与由实轴积分法[23]计算的结果对比,见图 5.在图 5算例中,轴对称发射-接收换能器用普通柱状(360°)声源模拟,中心频率20kHz,声源-接收器间距0.6096m(2ft);测井仪、井孔流体、套管和水泥环的外半径分别为20mm,60mm,70mm和100mm,换能器高度40mm;各介质声学参数见表 1;有限差分网格步长为Δr=4.0mm,Δz=8.021mm,Δθ=2.813°(0.0491rad),Δt=1.55×10-4 ms,NPML层厚度为15个网格.
|
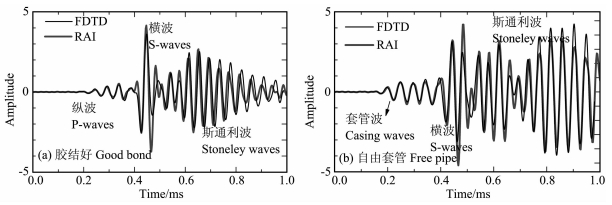
图 5 有限差分模拟波形和实轴积分法计算波形的对比 (a)胶结好,(b)自由套管. Fig. 5 Comparisons between the waveforms calculated by the FD method and the real-axis integration method (a) Good bond, and (b) free pipe. |
|
|
表 1 本文模型的声学参数 Table 1 Acoustic parameters of the model in this paper |
图 5a和图 5b分别为水泥环胶结好和完全缺失(自由套管)时两种方法计算波形对比.从图中可见对胶结好和自由套管两种情况,有限差分模拟的波形(细实线)与用实轴积分法计算的波形(粗实线)总体上一致性较好.两种方法得到的首波基本是重合的,横波和Stoneley波存在小的差异,其中幅度比相位符合程度略差.这可能是由于有限差分方法中声源的近似处理,以及网格有限小导致实际模型与输入参数存在微小偏差等因素造成的结果.此外由于实轴积分法中被积函数是由大量的用多项式逼近的贝塞尔函数组成,双重离散FFT实现的实轴积分计算也不是精确解值,也会有误差,因此这种数值检验确切的说是一种相互印证,只是实轴积分法广为应用,公认稳定可靠.可以认为上述比较的符合程度验证了并行有限差分方法的正确性、物理上的可信性.
3.2 SBT测井波形的数值模拟本节我们用并行有限差分算法模拟有水泥扇区缺失的套管井中8扇区SBT测井波形.为定位方便,我们定义第一对换能器(T1)为0°,水泥环扇区缺失的位置和大小可通过其中心相对T1的方位角(θA)和其角度大小(θS)定义,如图 6所示.以下的数值模拟中,发射换能器主频100kHz,声源-接收器间距0.6096m(2ft),记录的波形为接收换能器中心处的声压.测井仪、井孔流体、套管和水泥环的外半径分别为25mm,62mm,70mm和100mm,换能器高度40mm,声学参数见表 1.有限差分网格步长为Δr=1.0mm,Δz=2.0mm,Δθ=0.975°(0.0167rad),Δt=5.13×10-5 ms,NPML层厚度为12个网格.
|
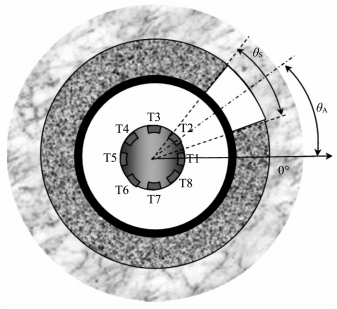
图 6 缺失的水泥扇区位置定义图 Fig. 6 Diagram for the definition of cement groove position |
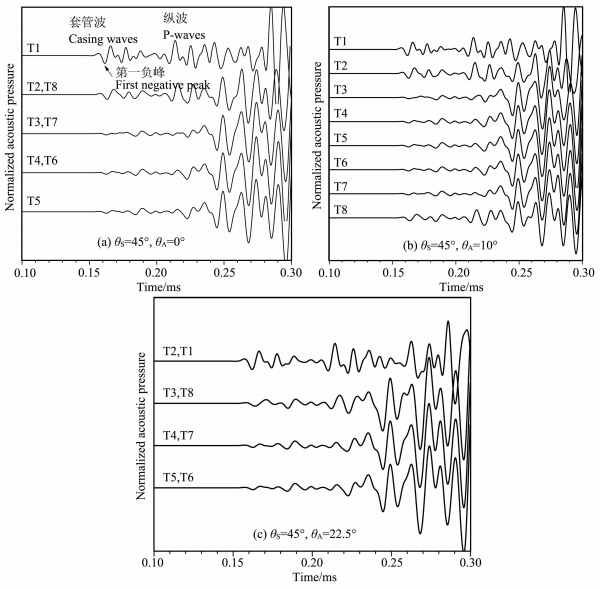
图 7中给出了扇区缺失大小为θS=45°时SBT测井模拟波形,方位角分别为(a)θA=0°,(b)θA=10°,(c)θA=22.5°.波形上所标T1-T8为产生该波形的换能器对序号(图 6).波形均按图 7a中T1测得波形最大值归一化.当两对换能器中心和缺失中心夹角相同时,它们测得的波形相同,被放在一起显示,如图 7a中的T2和T8.可以看到套管波以及地层纵波的幅度随着夹角的增大而减小.
|
图 7 套管井中水泥缺失扇区大小θS=45°时SBT测井波形 3张图分别为缺失在不同的方位:(a) θA=0°; (b) θA=10°; (c) θA=22.5° Fig. 7 Waveforms of SBT logging in cased hole with cement groove size θS=45°, and with azimuth (a) θA=0°, (b) θA=10° and (c) θA=22.5° |
在实际SBT测井中,测得的100kHz波形被调制为20kHz波形,然后计算20kHz波形一个周期的套管波幅度积分并记录下来,用来评价胶结质量.因此我们主要关心套管波幅度.作为理论研究,我们这里分析原始100kHz波形套管波头波的幅度以及套管波前5个周期的幅值积分,后者与实际SBT测井相比,都是相同时窗内套管波的幅度积分,反应相同的信息.
注意到相邻两对换能器间的夹角为45°,对于一定的θA,可以求出每对换能器和缺失扇区中心的夹角,例如当θA=10°,换能器T1-T8与缺失扇区间的夹角分别为10°,35°,80°,125°,170°,145°,100°,55°.因此对于某一大小为θS的缺失,我们可以分析套管波幅度随夹角的变化规律.
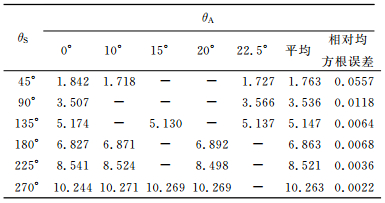
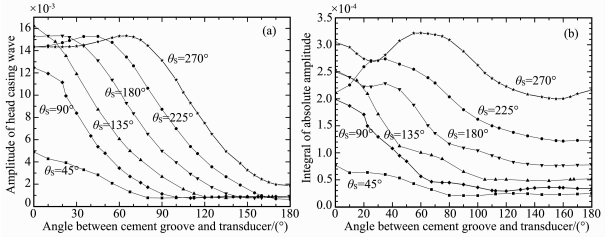
图 7中波形的分析结果在图 8中给出,为带有实心方块的线.图 8a为套管波头波的幅度(第一负峰幅值,以下简称幅度),图 8b为套管波前5个周期的积分值(以下简称幅度积分).当θS=90°,135°,180°,225°,270°时(方位角有所不同,见表 2),模拟波形的分析结果也在图 8中给出,由于篇幅限制,波形本身没有给出.
|
图 8 套管波幅度(a)和前5个周期绝对幅度积分(b)随夹角的变化曲线 Fig. 8 Amplitude of head casing wave (a), and the integral of absolute amplitude of first 5 cycles of the waveform (b), versus included angle |
|
|
表 2 不同大小和方位水泥缺失时套管波幅度8扇区平均值 Table 2 The average of casing wave amplitude of 8 sectors for various sizes and azimuths of cement groove |
在图 8a中,当缺失扇区θS≤135°时,幅度随夹角增大单调递减,当夹角较大时都趋于同一数值.而θS≥180°时,幅度曲线不再单调,最大值不在夹角0°处,且比θS=135°时最大值要小.这一现象应该是由于周向各方向套管波相互干涉叠加的结果.当夹角较大时,尤其是在180°附近,幅度对缺失大小不敏感.在图 8b中,幅度积分随夹角显示了与图 8a中相似的单调性和规律,只是对于较大的夹角,幅度积分随缺失增大而单调增大.
尽管对于同一大小的缺失,不同方向换能器得到的套管波幅度和幅度积分对夹角很敏感,而8对换能器幅度或幅度积分的平均值,应该依赖于缺失大小,而不受缺失的方位角的影响.表 2中的数据证实了这一推测.对于固定的缺失大小,缺失位于不同方位时得到的8对换能器平均值很接近,相对均方差非常小,且该平均值随缺失增大单调增大.经过分析,图 8b中显示幅度积分,也具有表 2中相同的特征.
以上模拟和分析结果显示,通过数值模拟建立如表 2和图 8的更详细的数据库或图板,由SBT测井8扇区幅度积分平均值可以直接反演水泥扇区缺失大小,然后利用图 8b中该缺失大小的幅度积分随夹角的变化曲线,缺失扇区相对换能器T1的方位可以通过最小二乘方法求得.为了得到较高的反演精度,就需要模拟各种扇区缺失大小(0°~360°)以及每一种缺失大小不同夹角(0~180°)时的波形,正演模拟数据越大,反演精度也就越高.这是一项计算量巨大的工作.本文给出的基于MPI的并行算法,相对串行算法计算速度可以提高数十倍,可以胜任这一工作.
4 结论我们给出了一种基于MPI的有限差分并行算法,用来模拟有扇区水泥缺失的非轴对称套管井中8扇区SBT测井的井孔瞬态声场.并行算法将有限差分网格根据计算机集群的条件任意分割为多个子区域,可以数十倍地提高计算速度.在轴对称情况下将有限差分并行算法模拟的波形和实轴积分法得到波形相对比,验证了方法和程序的正确性.用该方法模拟了各种大小和方位的扇区水泥缺失时8对换能器测得的波形,并分析了套管波头波幅度以及前5个周期幅度积分随换能器-缺失方位夹角的变化.得到了非轴对称套管井中8扇区SBT测井时弹性波传播的一些新的现象和规律,这些规律将有助于改进解释方法,从而提高SBT测井中水泥周向胶结情况的解释精度.可以在计算机集群上运行的基于MPI的并行有限差分算法,具有低投入、高性能的优点,可以应用于其他大规模波场模拟问题.
| [1] | Schoenberger M, Marzetta T, Aron J, et al. Space-time dependence of acoustic waves in a borehole. J. Acoust. Sot. Am. , 1981, 70(5): 1496-1507. DOI:10.1121/1.387107 |
| [2] | Chang S K, Everhart A H. A study of sonic logging in a cased hole. J. Pet. Tech. , 1983, 35(9): 1745-1750. DOI:10.2118/11034-PA |
| [3] | Tubman K M, Cheng C H, Toksöz M N. Synthetic full waveform acoustic logs in cased boreholes. Geophysics , 1984, 49(7): 1051-1059. DOI:10.1190/1.1441720 |
| [4] | Schmitt D P, Bouchon M. Full-wave acoustic logging:synthetic micro-seismograms and frequency-wavenumber analysis. Geophysics , 1985, 50(11): 1756-1778. DOI:10.1190/1.1441865 |
| [5] | 董庆德, 王克协. 柱状多层准弹性介质中声压波形的数值计算和分析-声法测井理论研究(Ⅱ). 地球物理学报 , 1985, 28(2): 208–217. Dong Q D, Wang K X. Numerical evaluation and analysis of the acoustic pressure waveform in cylindrical multilayer quasi elastic media. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1985, 28(2): 208-217. |
| [6] | Smolen J. Cased Hole and Production Log Evaluation. Pennwell Publishing Com., 1996. 161~191 |
| [7] | 张秀梅, 孙建孟, 陈雪莲. 扇区水泥胶结测井(SBT)响应的数值模拟. 测井技术 , 2004, 28(6): 515–517. Zhang X M, Sun J M, Chen X L. Numerical simulation of the logging response of Segmented Bond Tool (SBT). Well Logging Technology (in Chinese) , 2004, 28(6): 515-517. |
| [8] | 何峰江, 陶果, 王锡莉. 贴井壁声波测井仪的有限差分模拟研究. 地球物理学报 , 2006, 49(3): 923–928. He F J, Tao G, Wang X L. Finite difference modeling of the acoustic field by sidewall logging devices. Chinese J. Geophys. (in Chinese) , 2006, 49(3): 923-928. |
| [9] | 林伟军. 带扇形窜槽的非轴对称固井声场研究. 北京: 中国科学院声学研究所, 2004 . Lin W J. Acoustic field in a cased well with a sectorial crossing channel (in Chinese). Beijing: Institute of Acoustics, Chinese Academy of Science, 2004 . |
| [10] | 宋若龙. 非轴对称套管井声场并行计算及声波固井质量评价理论与方法研究. 长春: 吉林大学物理学院, 2008 . Song R L. Parallel computation of acoustic field in non-axisymmetric cased holes & theory and method studies of acoustic cementing quality evaluation (in Chinese). Changchun: College of Physics, Jilin Universiy, 2008 . |
| [11] | Stephen R A, Cardo Casas F, Cheng C H. Finite-difference synthetic acoustic logs. Geophysics , 1985, 50(10): 1588-1609. DOI:10.1190/1.1441849 |
| [12] | Randall C J. Multipole acoustic wave forms in nonaxisymmetric boreholes and formations. J. Acoust. Soc. Am. , 1991, 90(3): 1620-1631. DOI:10.1121/1.401903 |
| [13] | Cheng N Y, Cheng C H, Toksoz M N. Borehole wave propagation in three dimensions. J. Acoust. Soc. Am. , 1995, 97(6): 3483-3493. DOI:10.1121/1.412996 |
| [14] | Liu Q H, Schoen E, Daube F, et al. A three-dimension finite difference simulation of sonic logging. J. Acoust. Soc. Am. , 1996, 100(1): 72-79. DOI:10.1121/1.415869 |
| [15] | Chen Y H, Chew W C, Liu Q H. A three-dimensional finite difference code for the modeling of sonic logging tools. J. Acoustic. Soc. Am. , 1998, 103(2): 701-712. |
| [16] | Liu Q H, Sinha B K. A 3D cylindrical PML/FDTD method for elastic waves in fluid-filled pressurized boreholes in triaxially stressed formations. Geophysics , 2003, 68(5): 1731-1743. DOI:10.1190/1.1620646 |
| [17] | Sinha B K, Simsek E, Liu Q H. Elastic wave propagation in deviated wells in anisotropic formations. SEG 2006 Annual Meeting, 2006, 324~328 http://library.seg.org/doi/abs/10.1190/1.2358402 |
| [18] | Wang T, Tang X M. Finite-difference modeling of elastic wave propagation:A nonsplitting perfectly matched layer approach. Geophysics , 2003, 68(5): 1749-1755. DOI:10.1190/1.1620648 |
| [19] | 都志辉. 高性能计算并行编程技术-MPI并行程序设计. 北京: 清华大学出版社, 2001 . Du Z H. High-Performance Calculation Parallel Programming Techniques-MPI Parallel Programming (in Chinese). Beijing: Tsinghua University Press, 2001 . |
| [20] | Bohlen T. Parallel 3-D viscoelastic finite difference seismic modeling. Computers & Geosciences , 2002, 28(8): 887-899. |
| [21] | Blanch J O, Cheng A C, Varsamis G L. Attainable computational speed for large-scale seismic modeling on PC-based cluster. SEG Annual Meeting, Houston, Texas, 2005 http://library.seg.org/doi/pdfplus/10.1190/1.2148038 |
| [22] | Coutant O, Virieux J, Zollo A. Numerical source implementation in a 2D finite difference scheme for wave propagation. Bull. Seism. Soc. Am. , 1995, 85(5): 1507-1512. |
| [23] | Rosenbaum J H. Synthetic microseismograms:logging in porous formations. Geophysics , 1974, 39(1): 14-32. DOI:10.1190/1.1440407 |
 2010, Vol. 53
2010, Vol. 53