面波最早被天然地震学家们用于探测地球结构.近年,胡家富等[1]利用面波和接收函数联合反演滇西地区壳幔速度结构,何正勤等[2]研究了用微动中的面波信息来探测地壳浅部的速度结构,张智等[3]用地震面波频散重建了川滇地区壳幔S波速度,Chen等[4, 5]用地震面波频散重建了青藏高原壳幔S波速度与偏振各向异性结构.瑞雷波勘探同样也广泛应用于工程物探中,以探测表层的地质异常体,如地下土洞、溶洞、矿区废弃矿井以及各种地下掩埋物.为了研究面波波场特征及频散特性,不少学者进行了大量的正演模拟[6, 7]和频散曲线计算方法研究[8, 9].利用频散曲线反演介质速度结构的研究,从基于基阶曲线反演发展到多模式联合反演[10~12],大大提高了反演的精度.
高品质的地震面波记录为高精度的频散曲线提取提供了必要的前提条件,而如何采取有效的信号处理技术以提高频散曲线的提取精度和可靠性,是后续反演解释成败与否的关键因素之一.为此,多年来大量学者就此问题进行了不懈的努力和研究,提出了很多有效算法,取得了较好的应用效果.目前主要的频散曲线提取算法有相位差法[13]、τ-p变换算法(倾斜叠加算法)[14]、F-K变换算法[15]、时频分析法[16]和小波分析算法[17]等.Hyung-ChoonPark等[18]提出用谐波小波变换的方法来提取信号的相位谱,该方法具有一定的抗噪能力,但对多模式频散分析不具能力.
对于多模式联合反演则要求必须解决好如下两个主要问题:(1)在有规则干扰和随机噪声情况下,准确提取瑞雷波的频散曲线;(2)要求能同时准确提取多模式瑞雷波的各阶频散曲线.有一个不能有效实现,便会严重制约联合反演的正确性和精度.本文将对以上问题做研究.
2 基于拉东变换的频散分析方法二维连续函数d(x,t)的正演拉东变换用如下积分形式表示[19]:

|
(1) |
式中,x和t为输入变量,r和τ为变换变量.该积分形式沿轨迹表示为走时t和τ的线性函数.
拉东反变换的积分形式为
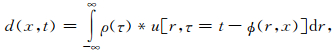
|
(2) |
在积分之前用ρ滤波器ρ(τ)与u(r,τ)进行褶积.对于二维数据类型d(x,t),ρ滤波器的傅里叶变换为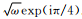
实际应用时,在时间空间域对资料进行离散采样,需要用离散叠加方程代替方程(1)和(2)中的积分形式,可以用最小二乘技术计算离散拉东变换[19].分析方程(1)中ϕ(r,x)的三种不同形式,相应地有三种拉东变换:双曲线拉东变换[20~22],抛物线拉东变换[23],线性拉东变换[20].这三种方法即是对三种不同函数型的同相轴进行变换,由于单频瑞雷面波的同相轴在波场中呈线性,故这里选择使用线性拉东变换.
对方程(1)作线性拉东变换时,函数φ(r,x)中的变换变量r代表射线参数p.那么,(x,t)和(p,τ)两种坐标系之间的关系可由下面的线性时差方程表示:

|
(3) |
式中,x为偏移距.将(3)式和p=1/v带入方程(1)中,即得:

|
(4) |
式中,t为传播走时,τ为p=0时的截距时间.从τ-p域到t-x域的变换为
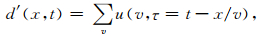
|
(5) |
要想由t-x域直接变换到f-v域,必须对式(5)中的t进行傅里叶变换:

|
(6) |
具体到u(v,f)和d′(x,f)中的每一个f成分,将方程(6)转为矩阵形式:

|
(7) |
式中L采用下面的复矩阵形式:

|
(8) |
L的大小为m×n,其中,m为面波分析的道数,n为速度参数的个数.d′和u为长度分别为m和n的复向量.可以看出矩阵L的元素依赖于观测系统确定的采集道数和构建速度叠加道集所需的速度值范围.
实现由t-x域到f-v域的变换,就是估算出u:u(v,f),标准的线性拉东变换为

|
(9) |
d为实际记录的傅里叶变换后得到的d(x,f)构成的一个长度为m的复向量.
上述标准线性拉东变换,具有明确的物理意义.为了使得d与拉东反变换得到的d′之间的差e:e(x,f)在最小二乘意义上最小.用矩阵符号和方程(7)表示e为
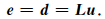
|
(10) |
方程(10)中的最小二乘解用累积平方误差S表示[24]:

|
(11) |
式中,T表示矩阵转置.将方程(10)带入(11)式可得:

|
(12) |
关于u求S的最小值,这样就得到了所期望的最小二乘解:

|
(13) |
(LTL)-1LT为L的最小二乘逆(也称广义逆).
方程(13)给出的是无约束的最小二乘解u.为了避免在矩阵LTL中出现奇异点或近奇异点,要对解加一些约束条件.将衰减因子β(也称为拉格朗日乘子)引入方程(13)[24]:

|
(14) |
由于复矩阵L有近奇异特征,特别是对于小值f,方程(14)给定的解可以用矩阵L的奇异值分解式(SVD)更好地表示[25].该过程矩阵L可用三个矩阵表示为

|
(15) |
利用L这种分解为因式的形式,方程(14)给定的约束解变为

|
(16) |
式中

|
(17) |
且Γi=λi/(λi2 +β),λi为LTL的特征值λi2的正平方根.衰减因子β是用来防止解方程(16)不稳定的.因此,若β选择恰当,用来提取面波频散关系就具有很强的抗干扰能力.此外,该方法能够分离出多模式面波的频散曲线,这为多模式面波频散曲线的联合反演提供了可靠的前提条件.
利用上述最小二乘奇异值分解线性拉东变换方法,即可将t-x域的面波记录变换到f-v域,其中v即是要求的面波相速度VR.对于基阶正频散曲线,可用如下视横波速度公式[26, 27],求取评价探测目标体异常情况的近似横波速度:

|
(18) |
式中,Ti为不同频率的周期,VS为视横波速度.利用该式可将面波相速度-频率曲线转换为视横波速度-频率频散关系,按照半波长关系H=λ/2解释,可获得视横波速度-深度剖面.利用介质视横波速度差异能够有效识别异常体的存在及其空间分布.
3 基于频散曲线的面波合成方法如何检验频散曲线求取方法的正确性、稳定性,评价各种方法的合理性、适用范围和深入认识复杂介质面波波场特征从而做出更合理的地质解释显得尤为重要.为此,提出了基于频散曲线合成理论瑞雷面波地震记录的方法来解决以上问题.
3.1 子波的选取研究面波的频散特性,为便于分析各频率成分的面波的能量变化,设子波各频率成分能量相等.因此,选择抽样脉冲信号作为面波记录合成用子波,其时间函数为[28, 29]:

|
(19) |
式中f0为上限频率.抽样脉冲信号时域波形图如图 1a所示,其频谱函数为

|
(20) |
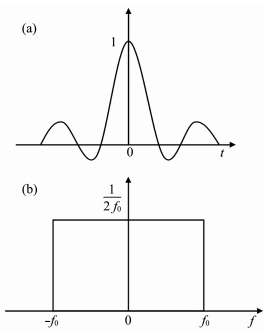
|
图 1 抽样脉冲信号 (a)波形图;(b)振幅谱. Fig. 1 Sampling pulse signal (a) Waveform graph; (b) Amplitude spectrum. |
式中A(f)为振幅,f为频率.其振幅谱如图 1b所示.由(20)式可知抽样脉冲信号的频谱函数虚部为零,相位恒等于零,是一零相位信号.用此信号作为震源子波,其频带宽度可根据频散曲线上限频率来确定,此外各频率成分能量分布均匀且具有分辨率最高等优点.
3.2 面波合成的原理选择抽样脉冲信号作为子波,设其上限频率为f0,则面波不同频率成分的传播时间为

|
(21) |
式中v(f)是由频散曲线决定的面波相速度.设最小炮间距为x0,Δx为道间距,则第n道的相位为

|
(22) |
式中φ0(f)为子波初相位,tn(f)是面波从激发点传至第n道所需的时间:

|
(23) |
则相邻道记录的相位差为

|
(24) |
由上可得第n道信号的频谱函数为

|
(25) |
A(f)为抽样脉冲信号的振幅谱.若子波初相位φ0(f)=0,则上式变为:

|
(26) |
对式(25)或(26)式做反傅里叶变换即得第n道面波记录.对于多阶模式第n道面波记录的合成可表示为

|
(27) |
式中,I为多模阶数,i表示第i阶,vi(f)为第i阶频散关系曲线.因此,只要设定子波的上限频率、总道数、道距、最小炮间距、采样间隔及记录长度,根据式(27)即可合成多阶模式纯面波单炮地震记录.
4 模型信号分析实际瑞雷波勘探大多存在多模式,利用多模式联合反演解释会取得很好的地质效果.为此,要求能够精确地提取出多模式的各阶频散曲线,这不仅要求频散提取方法要有较强的抗干扰能力,还必须具有较高速度分辨率.给定四层层状土层介质模型(表 1)用改进的传播矩阵法[27]计算的各阶频散曲线如图 2(只计算了低阶的4个模式).利用上述基于频散曲线合成瑞雷面波方法,选择上限截止频率120 Hz、采样率0.5ms、道间距0.5m、记录长度1s、接收道数100,由式(27)合成有一、二、三、四阶的多模面波记录如图 3所示.对合成的多模式面波记录,选择合适的参数,用最小二乘奇异值分解线性拉东变换进行频散分析,得到如图 4所示的频散能量谱(便于对比分析,模型计算理论频散曲线附予其中).
|
|
表 1 四层层状土层介质模型特性参数 Table 1 The parameters of four-layered soil medium model |
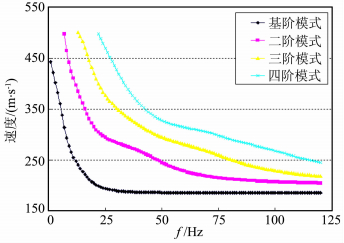
|
图 2 正演计算的多模式频散曲线(表 1模型) Fig. 2 The high-mode frequency dispersion curves by forward calculation (the model of table 1) |
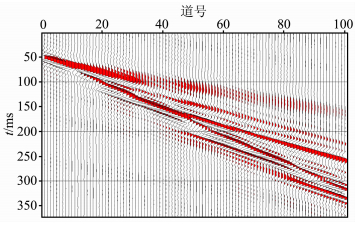
|
图 3 合成面波记录(图 2多模式频散曲线) Fig. 3 The synthetic surface wave record (The high-mode velocity dispersion curves showed in Fig. 2) |

|
图 4 拉东变换法提取的多模式频散能量谱(图 3记录) Fig. 4 The high-modes frequency dispersion energy spectrum by Radon Transform (the record showed in Fig. 3) |
模型分析表明,在没有干扰的情况下,最小二乘奇异值分解线性拉东变换频散分析法对多模式的存在能够取得较满意的结果,而且速度分辨率很高.该方法是以频域叠加能量的强弱识别信号的频散曲线的,在低频部分由于接收道距小分辨率略低,强能量团与理论值有一定的偏差.在有各种干扰存在时,改变求解方程(16)中的衰减因子β的大小,选择恰当的值可提高该方法的抗干扰能力.这为多模式频散曲线联合反演提供了很好的基础,有助于获得更好的勘察效果.
5 实际资料处理为了对某大桥地基土层的性质进行评价,进行了瑞雷波勘探.采用道距4m、24道的排列接收,点距20m,共12个点.采用震源枪激发,面波能量明显占优,信噪比较高.采集的地震记录如图 5所示,根据该区地质条件及原始记录的速度和频率分析结果,选择分析参数为:分析频率范围3~50 Hz,速度范围50~500m/s,频率扫描间隔1Hz,速度扫描间隔1m/s.对某测点原始记录进行频散分析,得图 6所示归一化频散能量谱.从图中可见,可靠的低频信号为5Hz,高阶振型在高频部分能量很强,但不影响低阶模式信号的频散分析.因此,可准确分离出基阶模式频散曲线.本文未对多模式联合反演进行研究,反演解释依旧采用基阶频散曲线,对12个测点分别进行相同的分析并提取出基阶频散曲线如图 7所示.最后,根据式(18)相速度和视横波速度的关系,并做时-深转换,将每个排列的中点位置作为这个排列的测点,可得如图 8所示的视横波速度剖面,通过图 8能够有效评价该区地基土层结构性质,为桥墩建立地基处理提供了可靠的地质依据.

|
图 5 测线某点面波地震记录 Fig. 5 One surface wave seismic record in the exploration line |

|
图 6 图 5所示面波地震记录的频散能量谱 Fig. 6 The frequency dispersion energy spectrum of the surface wave seismic record showed in Fig. 5 |

|
图 7 各测点的基阶频散曲线 Fig. 7 The fundamental frequency dispersion curves of all points |

|
图 8 测线视横波速度剖面 Fig. 8 The pseudo S-wave velocity profile of the exploration line |
瑞雷面波频散曲线计算.研究提出了基于频散曲线的面波合成方法,对计算出的多模式频散曲线进行了面波记录合成,并采用改进的抗干扰最小二乘奇异值分解线性拉东变换进行频散分析,取得了很好的速度分辨率,能够准确地提取出多模式面波的各阶频散特性曲线.
本文所研究的频散分析方法,不对原始记录进行数字处理(时域滤波、FK滤波),避免了数字处理效应的影响(如吉普斯效应等),而是通过对信号的频谱分析、结合场地的地质条件,通过选择频散分析的频率、速度范围,来达到规避高视速度的直达波、反射波等干扰.模型和实际资料分析表明,该方法具有抗干扰能力强,能够高精准地分离出多模式面波的各阶频散特性曲线,可利用分离出的基阶模式的频散曲线进行反演,同时为多模式联合反演提供了可靠的各阶频散特性曲线.
| [1] | 胡家富, 朱雄关, 夏静瑜, 等. 利用面波和接收函数联合反演滇西地区壳幔速度结构. 地球物理学报 , 2005, 48(5): 1069–1076. Hu J F, Zhu X G, Xia J Y, et al. Using surface wave and receiver function to jointly inverse the crust-mantle velocity structure in the West Yunnan area. Chinese J. Geophys. (in Chinese) , 2005, 48(5): 1069-1076. DOI:10.1002/cjg2.750 |
| [2] | 何正勤, 丁志峰, 贾辉, 等. 用微动中的面波信息探测地壳浅部的速度结构. 地球物理学报 , 2007, 50(2): 492–498. He Z Q, Ding Z F, Jia H, et al. To determine the velocity structure of shallow crust with surface wave information in micro tremors. Chinese J. Geophys. (in Chinese) , 2007, 50(2): 492-498. |
| [3] | 张智, 陈赟, 李飞. 利用地震面波频散重建川滇地区壳幔S波速度. 地球物理学报 , 2008, 51(4): 1114–1122. Zhang Z, Chen Y, Li F. Reconstruction of the S-wave velocity structure of crust and mantle from seismic surface wave dispersion in Sichuan-Yunnan Region. Chinese J. Geophys. (in Chinese) , 2008, 51(4): 1114-1122. |
| [4] | Chen Y, Badal J, Zhang Z J. Radial anisotropy in the crust and upper mantle beneath the Qinghai-Tibet Plateau and surrounding regions. Journal of Asian Earth Sciences , 2009, 36: 289-302. DOI:10.1016/j.jseaes.2009.06.011 |
| [5] | Chen Y, Badal J, Hu J F. Love and Rayleigh wave tomography of the Qinghai-Tibet Plateau. Pure and Applied Geophysics , 2010, 167(10). DOI:10.1007/s00024-009-0040-1 |
| [6] | 周竹生, 刘喜亮, 熊孝雨. 弹性介质中瑞雷面波有限差分法正演模拟. 地球物理学报 , 2007, 50(2): 567–573. Zhou Z S, Liu X L, Xiong X Y. Finite-difference modelling of Rayleigh surface wave in elastic media. Chinese J. Geophys. (in Chinese) , 2007, 50(2): 567-573. |
| [7] | 周红, 陈晓非. 凹陷地形对Rayleigh面波传播影响的研究. 地球物理学报 , 2007, 50(4): 1182–1189. Zhou H, Chen X F. A study on the effect of depressed topography on Rayleigh surface wave. Chinese J. Geophys. (in Chinese) , 2007, 50(4): 1182-1189. |
| [8] | 何耀锋, 陈蔚天, 陈晓非. 利用广义反射-透射系数方法求解含低速层水平层状介质模型中面波频散曲线问题. 地球物理学报 , 2006, 49(4): 1074–1081. He Y F, Chen W T, Chen X F. Normal mode computation by the generalized reflection-transmission coefficient method in planar layered half space. Chinese J. Geophys. (in Chinese) , 2006, 49(4): 1074-1081. |
| [9] | 邵广周, 李庆春, 梁志强. 液体表层层状介质导波频散曲线研究. 地球物理学报 , 2007, 50(3): 915–920. Shao G Z, Li Q C, Liang Z Q. A study on dispersion curves of guided wave in layered media with overlying liquid surface. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 915-920. |
| [10] | 陈祥, 孙进忠. 改进的等效半空间法及瑞雷波频散曲线反演. 地球物理学报 , 2006, 49(2): 569–576. Chen X, Sun J Z. An improved equivalent homogenous half-space method and reverse fitting analysis of Rayleigh wave dispersion curve. Chinese J. Geophys. (in Chinese) , 2006, 49(2): 569-576. |
| [11] | 鲁来玉, 张碧星, 汪承灏. 基于瑞利波高阶模式反演的实验研究. 地球物理学报 , 2006, 49(4): 1082–1091. Lu L Y, Zhang B X, Wang C H. Experiment and inversion studies on Rayleigh wave considering higher modes. Chinese J. Geophys. (in Chinese) , 2006, 49(4): 1082-1091. |
| [12] | 罗银河, 夏江海, 刘江平, 等. 基阶与高阶瑞利波联合反演研究. 地球物理学报 , 2008, 50(1): 242–249. Luo Y H, Xia J H, Liu J P, et al. Joint inversion of fundamental and higher mode Rayleigh waves. Chinese J. Geophys. (in Chinese) , 2008, 50(1): 242-249. |
| [13] | 杨成林. 瑞雷波勘探. 北京: 地质出版社, 1993 . Yang C L. Rayleigh-waves Exploration (in Chinese). Beijing: Geological Publishing House, 1993 . |
| [14] | 宋先海, 肖柏勋, 顾汉明, 等. 用改进的τ-p变换算法提取瞬态瑞雷波频散曲线. 物探与化探 , 2003, 27(4): 292–295. Song X H, Xiao B X, Gu H M, et al. The application of improved τ-p transform algorithm to the extraction of dispersion curve of transient Rayleigh waves. Geophysical & Geochemical Exploration (in Chinese) , 2003, 27(4): 292-295. |
| [15] | Gabriels P, Snieder R, Nolet G. In situ measurements of shear-wave velocity in sediments with higher-mode Rayleigh waves. Geophysical Prospecting , 1987, 35: 187-196. DOI:10.1111/gpr.1987.35.issue-2 |
| [16] | 鲁来玉, 汪承灏, 张碧星. 分层介质半空间瑞利波的时频分析. 声学学报 , 2006, 31(5): 425–432. Lu L Y, Wang C H, Zhang B X. Time-frequency analysis of the dispersive Rayleigh waves in stratified media. Acta Acustica (in Chinese) , 2006, 31(5): 425-432. |
| [17] | 彭文, 王亮. 瑞雷面波频散特征的时频分析方法及应用. 物探化探计算技术 , 2006, 28(3): 233–239. Peng W, Wang L. Theory and application of Time-frequency analysis to Rayleigh waves prospecting. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 2006, 28(3): 233-239. |
| [18] | Hyung-Choon Park, Sung-Eun Joh. Determination of phase spectrum using harmonic wavelet transform. NDT & E International , 2009, 42: 534-542. |
| [19] | Beylkin G. Discrete Radon transform:IEEE Trans. on Acoustics, Speech and Signal Processing. AASP , 1987, 35: 162-179. DOI:10.1109/TASSP.1987.1165108 |
| [20] | Thorson J R, Claerbout J F. Velocity-stack and slant-stack stochastic inversion. Geophysics , 1985, 50: 2727-2741. DOI:10.1190/1.1441893 |
| [21] | Yilmaz O. Velocity-stack processing. Geophys. Prosp. , 1989, 37: 357-382. DOI:10.1111/gpr.1989.37.issue-4 |
| [22] | Foster D J, Moshcr C C. Suppression of multiple reflections using the Radon transform. Geophysics , 1992, 57: 386-395. DOI:10.1190/1.1443253 |
| [23] | Hampson D. Inverse velocity stacking for multiple elimination. J. Can. Soc. Expl. Geophys , 1986, 22: 44-55. |
| [24] | Lines L R, Treitel S. Tatoriah. A review of least-squares inversion and its application to geophysical problems. Geophys. Prosp. , 1984, 32: 159-186. |
| [25] | Press W H, Flannery B P, Teukolsky S A, et al. Numerical Recipes:The Art of Scientific Computing. London:Cambridge University Press. 1986 |
| [26] | 姜建国, 曹建中, 高玉明. 信号与系统分析基础. 北京: 清华大学出版社, 1994 : 85 -91. Jiang J G, Cao J Z, Gao Y M. The Basis of Signal and System Analysis (in Chinese). Beijing: Tsinghua University Press, 1994 : 85 -91. |
| [27] | 凡友华, 陈晓非, 刘雪峰, 等. Rayleigh波的频散方程高频近似分解和多模式激发数目. 地球物理学报 , 2007, 50(1): 233–239. Fan Y H, Chen X F, Liu X F, et al. Approximate decomposition of the dispersion equation at high frequencies and the number of multi-modes for Rayleigh waves. Chinese J. Geophys. (in Chinese) , 2007, 50(1): 233-239. |
| [28] | 凌甦群, 三轮滋.瞬态面波法和微动勘探法在日本新滴县中越地震灾区地质调查中的应用.见:刘云祯主编.工程物探新技术.北京:地质出版社, 2006.80~85 Ling S Q, Miwa S. The evaluation of soil structures by surface wave prospecting method and microtremor survey method-2004 Mid Niigata prefecture earthquake.In:Liu Y Z ed.A New Technique on Engineering Geophysical Method.Beijing:Geological Publishing House, 2006.80~85 |
| [29] | 徐佩芬, 凌甦群. 微动技术探测煤矿陷落柱的原理方法及效果. 地球物理学报 , 2009, 52(7): 1923–1930. Xu P F, Ling S Q. The principle and effect s of exploration technique for microt remor in coal mine fall column. Chinese J. Geophys. (in Chinese) , 2009, 52(7): 1923-1930. |
 2010, Vol. 53
2010, Vol. 53


