2. 成都理工大学"油气藏地质及开发工程"国家重点实验室, 成都 610059
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu University of Technology, Chengdu 610059, China
叠前偏移后的地震数据较叠后偏移数据更能真实地反映地下构造形态及地下反射面的位置及岩性变化[1].但在横向速度变化剧烈的复杂区域,即使采用共偏移距或共炮集Kirchhoff偏移,也会产生一些意想不到的运动学与动力学假像.Duquet[2]在研究二维Marmousi时注意到:使用正确速度模型,用波动方程计算格林函数的共偏移距道集时存在假像,且同相轴并不平,这不仅使复杂地质构造下的速度建模变得很困难,更让AVO分析陷入绝境.
为了克服偏移过程中存在的假象,提高精确成像的质量,需要在共反射角度域对成像道集进行重建[3].1990年,DeBruin等[4]提出了利用平面波道集偏移成像得到平面波参数域成像道集.2001年,Prucha等[5]在炮域和偏移距域证明多波至的运动学问题,并提出了通过波动方程偏移重构获得共成像角道集的方法.2003年,Sava和Fomel[6]利用单程波偏移成像中的双平方根方程并结合倾斜叠加,提出了一种波动方程角度域共成像道集.在国内,陈生昌等[7]、陈凌等[8]对角度域成像进行了研究,并在理论模型和实际数据中取得较好效果.
共偏移距道集已被广泛地应用于地震速度建模及振幅随偏移距变化(AVO)的研究中[9],但复杂构造及射线多路径产生的共偏移距道集不保幅性等一系列缺陷给AVO研究带来很大的困难.
共反射角道集包含有能反映地下速度和岩性变化的信息,更有利于速度模型优化、地震振幅属性分析及地下岩性和断裂的研究[10~12].本文通过研究共反射角深度偏移方法和理论,完善了基于目标的共反射角深度偏移技术,提出了获得相对保幅共反射角道集方法.该方法克服了偏移距域道集在复杂介质中遇到的困难,更能有效地反映波场和地质结构方面的信息.通过理论模型数据进行了试算,并采用实际地震数据对此方法进行了验证,在陡倾角成像方面取得较好效果.通过研究认为共反射角道集更有利于地震速度建模、速度模型优化及AVA分析,为今后叠前反演及岩性预测提供新的研究方向.
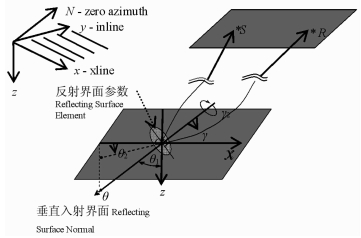
2 方法原理在深度域,对地震成像点进行逐点运算.在每个成像点o*激发后可得到一簇扇形状的上行射线束(图 1),且这簇射线束具有均匀的临界角增量,走时、几何扩散以及相位因子可根据每个射线束片段计算获得[13].
|
图 1 反射角偏移示意图 Fig. 1 Sketch map of common reflection angle domain migration |
根据共反射角道集(CRA)内给定的地震道,对所有地震成像点进行逐点求和后,可获得角度域成像数据.这些射线对都来源于地下成像点o*,但这些射线来自于共成像点不同的方向(地层倾角用θ表示),它们都具有相同的反射角γ(开角的一半).
共反射点成像公式[14]如下:
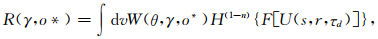
|
(1) |
式中s与r表示炮点与检波点的位置,即当射线到达地面时,波至点附近炮检点位置,可以用函数s(θ,γ,o*)与r(θ,γ,o*)表示,τd(θ,γ,o*)为走时时间,H为希尔伯特变换,n为指数[13],F[U(s,r,τd)]为地震波场函数,振幅加权因子表示如下:
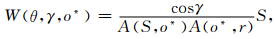
|
(2) |
其中:
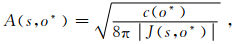
|
(3) |
c(o*)代表成像点速度,J(s,o*)为几何扩散度函数.S为格林函数的源符号.
一般情况下,对于给定的反射角,在波至附近,其偏移距对应的所有地震数据都对角度偏移道集有贡献.每个成像点的偏移孔径可根据反射层的法线矢量方向获取.根据傍轴射线理论,获取量的小偏移孔径,作为第一菲涅尔带的空间投影,并且此菲涅尔带是成像目标到数据空间的距离[15].用该方法在地震成像点上进行偏移求和.在这些成像点上,炮点位置、检波点位置及双程走时都是从地层倾角与反射角出发,且在成像点处的倾角和反射角都均匀[16].
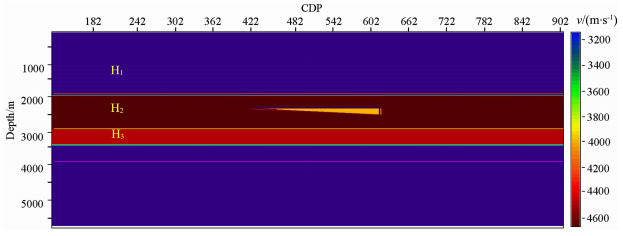
3 理论模型数值算例 3.1 楔状模型试算根据地震速度建模方法[17]和共反射角深度成像计算精度设计了理论模型(图 2).通过2D理论模型数据对偏移方法进行了试算,对反射角偏移计算的稳定性、精度及速度模型纵横向变化的适应性等进行验证.理论模型在空间由三层组成,其每一层的速度及深度如下:
|
图 2 理论模型示意图 Fig. 2 Sketch map of theoretical model |
H1:VP=3000m/s,H=0~2000m;H2:VP=4700m/s,H=2000~3000 m(图 2中楔状模型);VP=4000m/s,H=2400~2600m;H3:VP=4500m/s,H=3000~4000m.
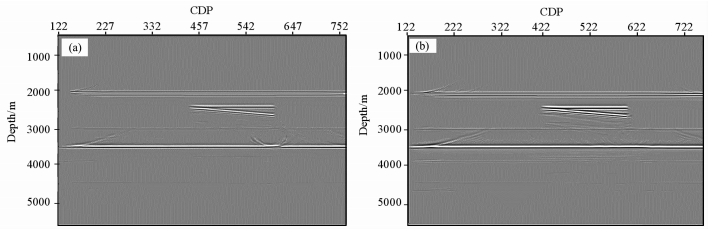
图 3所示,理论模型试算结果表明,特殊地质体及下覆地层均能准确归位成像.但在未应用相位旋转因子时(图 3a),低速楔状模型侧向与垂向速度变化剧烈,成像效果稍差[5].在物理上焦散射线场是折叠射线场的相移之和,通常情况下,折叠射线族中的每一个分支都有相同的焦散场标记值,但相同标记值的射线并不一定属于射线族的同一分支[18].针对二维理论模型,采用公式(3)中几何扩散度J,渐近振幅A,可以改进实际数据中的振幅保真性(图 3b应用相位旋转因子),改善成像效果.
|
图 3 共反射角叠前深度偏移理论模型试算结果 (a)未应用相位旋转因子;(b)应用相位旋转因子. Fig. 3 Calculation results of pre-stack migration of common reflection angle (a) Before applying phase rotation factor; (b) After applying phase rotation factor. |
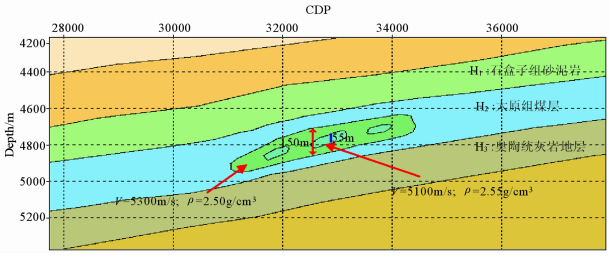
根据礁滩体岩性特征(图 4),利用纵波速度、横波速度和密度等资料,建立一个礁体层状介质模型(图 4).在模型中,自下而上为二叠系石盒子组砂泥岩、太原组煤层和奥陶系中奥陶统及下奥陶统灰岩地层,各层模型物理参数如下:
|
图 4 礁体模型及参数图 Fig. 4 The model and parameters of reef body |
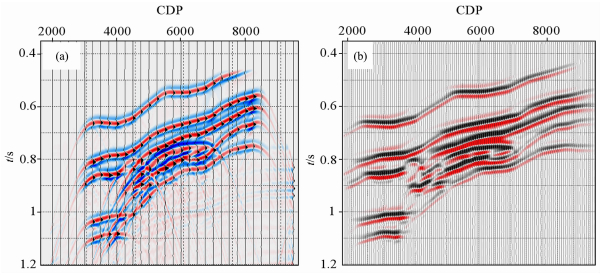
H1:石盒子组砂泥岩(包括上覆地层),VP=4200m/s,ρ=2.45g/cm3;H2:太原组煤层,VP=4500m/s,ρ=2.40g/cm3;(异常体:VP=5100m/s,ρ=2.55g/cm3,厚度50m);H3:奥陶统灰岩(包括下覆地层),VP=5600m/s,ρ=2.60g/cm3.利用礁体模型研究礁滩相地层的地震响应特征.利用弹性波波动方程的方法模拟野外放炮,得到零偏移距剖面(图 5a).图 5b为共反射角叠前深度偏移剖面,礁体反射特征为两峰夹一谷.在礁体内部出现亮点反射,且礁体具有明显的丘状反射特征.
|
图 5 礁体模型正演零偏移距剖面(a)与共反射角叠前偏移结果(b) Fig. 5 Zero-offset profile of reef body model (a) and resutt of pre-stack migration of common reflection angle (b) |
本文所采用的实际数据是我国西部某油田的资料,地下构造比较复杂.在速度模型建立中采用相干反演法建立初始速度模型.通过Kirchhoff积分法在共偏移距道集上对速度模型进行迭代,最后基于共角度域道集,对速度模型进行剩余延迟分析及速度模型优化[19].
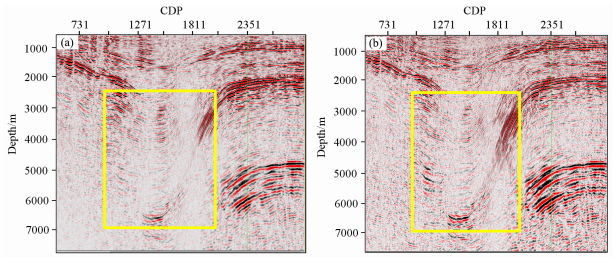
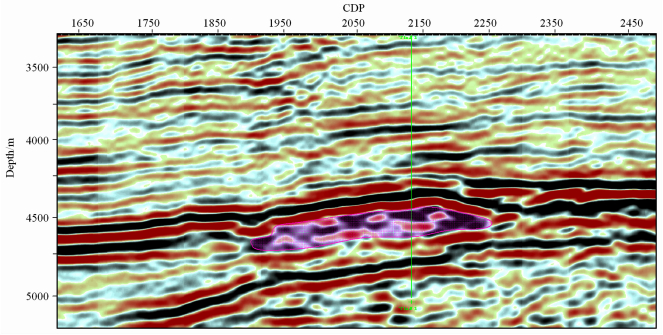
通过分析Kirchhoff深度偏移与共反射角深度偏移结果(图 6)对比,可以看出共反射角偏移成像的效果较理想,向斜部位成像、断点归位及一些构造细节得到改善,特别在陡倾角成像方面共反射角偏移比Kirchhoff更有优势.图 7所示共反射角深度偏移更有利于异常体聚焦成像,异常体反射特征清楚,礁体具有明显的丘状反射特征(图 4的礁体模型也证实这点).
|
图 6 Krchhoff深度偏移(a)与共反射角深度偏移(b)对比 Fig. 6 Comparison of Kirchhoff pre-stack migration (a) and pre-stack migration of common reflection angle (b) |
|
图 7 共反射角叠前深度偏移结果(实际资料) Fig. 7 Resutt of pre-stack migration of common reflection angle (real data) |
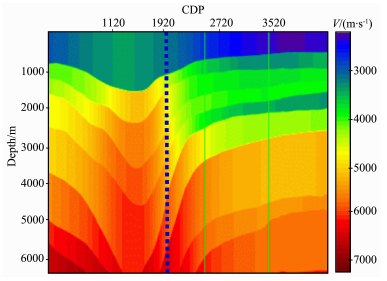
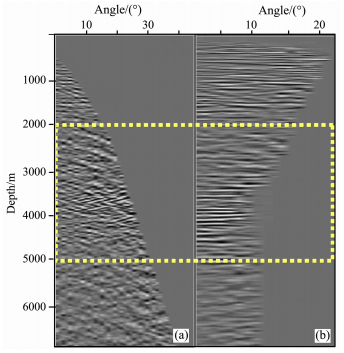
通过对复杂介质偏移成像的分析,可以对复杂介质中定量偏移增加理解.共偏移距道集的缺点和共偏移距成像中的假像,在共偏移距偏移时无法解决.陡倾角部位(图 8中CDP1920位置)如图 9所示,共偏移距道集反射杂乱,但共反射角道集很清楚.共反射角偏移的优势不仅体现在成像质量上,更重要的是反射角道集包含岩性信息,有利于AVA分析及偏移速度分析.最近研究表明,即使在共反射角度域里,射线偏移还存在假象,这是因为在无穷高频的情况下,若存在焦散场,则对单一的参数积分不能消除假象.无假象的共角度成像道集可以由双平方根波动方程偏移计算得到[20, 21].在Kirchhoff偏移中,可以通过同相轴斜率加权,较好地清除假象.无论如何,采用共反射角度域深度偏移时产生的假象比共偏移距深度偏移少很多.
|
图 9 Kirchhoff深度偏移CRP (a)与共反射角深度偏移CRA (b)对比 Fig. 9 Comparison of Kirchhoff pre-stack migration CRP (a) and pre-stack migration of common reflection angle CRA (b) |
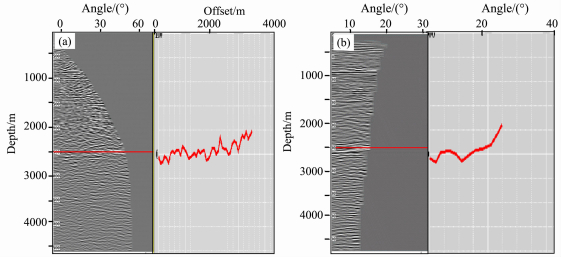
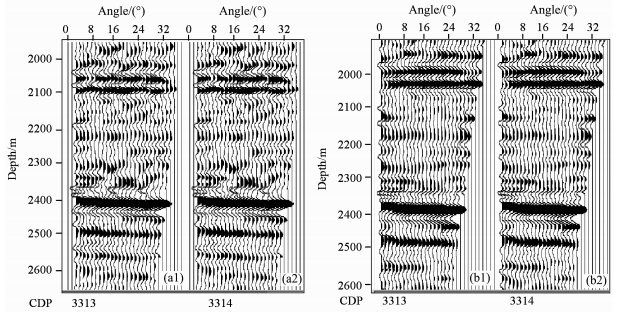
当地下结构很复杂时,在深度域进行振幅随偏移距变化分析具有很大优势,而共反射角度域偏移直接给出振幅随反射角的变化(图 10b),共反射角道集AVO特征更加直观明显,更有利于AVA分析及叠前反演研究(图 10).通过对CRP构建的角道集与共反射角道集(图 11)对比可看出,CRP构建角度道集时,无法构建小角度(0°~3°),同时道集存在噪音.而共反射角的道集(CRA)能克服上述缺陷,更有利于地层岩性的研究.共反射角道集通过倾角求和构建,因此需要从成像点向地表发送射线,当射线到达地面时,应在实际位置对地震数据进行插值并加入倾斜叠加,则可消除上述假象[22, 23].如图 10、图 11所示,在复杂区域的共反射角道集,无论是从振幅均衡、AVO响应,还是消除假象的角度来讲,较共偏移距道集有了很大的改善.同时在速度分析方面,共反射角度域偏移是复杂情况下合理的共像集,给层析成像带来新机遇.
|
图 10 Krchhoff深度偏移CRP道集(a)与共反射角深度偏移CRA道集(b) AVO特征对比 Fig. 10 AVO of Kirchhoff pre-stack migration CRP (a) and pre-stack migration of common reflection angle CRA (b) |
|
图 11 CRP构建角度道集与共反射角道集特征对比(CDP3313、3314) (a1,a2)由CRP构建角道集;(b1,b2)共反射角道集 Fig. 11 Comparison of angle gathers constructed from CRP and common reflection angle gathers CRA (a1, a2) Angle gathers constructed by CRP; (b1, b2) Common reflection angle gathers |
共偏移距道集在复杂介质中因地震波传播的多路径而造成地下反射体位置成像不准确,共反射角道集(CRA)克服了上述缺陷而逐步成为复杂区精确成像、AVA分析及保幅偏移成像研究的主要手段.
通过对基于模型的共反射角成像方法及速度模型建立的研究,构建真正的角度域道集.从本文的数值试算及实际资料共反射角深度偏移处理中可以看出,以目标为导向的共反射角成像方法对复杂速度模型及地质模式有很强的适应性.特别是在宽反射角、甚至具有多波至复杂构造区,反射同相轴的振幅和相位得到有效的保护.在陡倾角成像上比Kirchhoff偏移更有优势.更重要的是共反射角的道集(CRA)能克服共偏移距道集的缺陷,更有利于速度建模、地层岩性及断裂体系的研究,为基于角度域的AVA分析提供新的研究方向.
| [1] | 陈生昌, 马在田, WuRushan. 波动方程角度域共成像道集. 地球科学 , 2007, 32(4): 569–573. Chen S C, Ma Z T, Wu R S. Angle domain common image gather for wave equation. Earth Science-Journal of China University of Geosciences (in Chinese) , 2007, 32(4): 569-573. |
| [2] | Duquet B, Ehinger A, L Uv P.A new imaging techniqu e for reliable mi gration velocity analysis.64 Ann.Interuat.Mtg.Soc.Expl.Geophys., Expanded Abstracts, 1994.1187~1190 http://www.osti.gov/scitech/biblio/89726 |
| [3] | Xu S, Chauris H, Lambare G, Noble M. Common angle image gather:a strategy for imaging complex media. Extended Abstracts, Soc.Expl.Geophys, 1998.1538~1541 http://www.earthdoc.org/publication/publicationdetails/?publication=14033 |
| [4] | De Bruin C G M, Wapenaar C P A, Berkhout A J. Angle-dependent reflectivity by means of prestack migration. Geophysics , 1990, 55(9): 1223-1234. DOI:10.1190/1.1442938 |
| [5] | Prucha M, Biondi B, Symes W. Angel-domain common image gather by wave-equation migration. Extended Abstracts, Soc.Expl.Geophys, 2001.824~827 |
| [6] | Sava P, Fomel S. Angle domain common image gathers by wave field continuation methods. Geophysics , 2003, 68(3): 1065-1074. DOI:10.1190/1.1581078 |
| [7] | 陈生昌, 曹景忠, 马在田. 叠前地震数据的平面波深度偏移法. 地球物理学报 , 2003, 46(6): 821–826. Chen S C, Cao J Z, Ma Z T. A method of plane wave depth migration for pre-stack seismic data. Chinese J. Geophys. (in Chinese) , 2003, 46(6): 821-826. |
| [8] | 陈凌, 吴如山, 王伟君. 基于Gabor-Daubechies小波束叠前深度偏移的角度域共成像道集. 地球物理学报 , 2004, 47(5): 876–884. Chen L, Wu R S, Wang W J. Common angle image gathers obtained from Gabor-Daubechies beamlet prestack depth migration. Chinese J. Geophys. (in Chinese) , 2004, 47(5): 876-884. |
| [9] | 王西文, 刘全新, 苏明军, 等. 多井约束下的速度建模方法和应用. 石油地球物理勘探 , 2003, 38(3): 263–367. Wang X W, Liu Q X, Su M J, et al. Multi-well constrained velocity model-building method and its application. Oil Geophysical Prospecting (in Chinese) , 2003, 38(3): 263-367. |
| [10] | Xu S, Chauris H, LambaréG, Noble M. Common angle migration:A strategy for imaging complex media. Geophysics , 2001, 66(6): 1877-1894. DOI:10.1190/1.1487131 |
| [11] | 张宇. 振幅保真的单程波方程偏移理论. 地球物理学报 , 2006, 49(5): 1410–1430. Zhang Y. The theory of true amplitude one-way wave equation migration. Chinese J. Geophys. (in Chinese) , 2006, 49(5): 1410-1430. |
| [12] | 王西文, 杨孔庆, 周立宏, 等. 基于小波变换的地震相干体算法研究. 地球物理学报 , 2002, 45(6): 847–852. Wang X W, Yang K Q, Zhou L H, et al. Methods of calculating coherence cube on the basis of wavelet transform. Chinese J.Geophys. (in Chinese) , 2002, 45(6): 847-852. |
| [13] | Thomson C J, Chapman C H.. An introduction to Maslov's asymptotic method. Geophys. J. R. Astr. Soc. , 1985, 83(1): 143-168. DOI:10.1111/j.1365-246X.1985.tb05161.x |
| [14] | Miller D, Oristaglio M, Beylkin G. A new slant on seismic imaging:migration and integral geometry. Geophysics , 1987, 52(7): 943-964. DOI:10.1190/1.1442364 |
| [15] | Schleicher J, Hubral P, Tygel M, et al. Minimum apertures and Fresnel zones in migration and demigration. Geophysics , 1997, 62: 183-194. DOI:10.1190/1.1444118 |
| [16] | Koren Z, Kosloff D.Common reflection angle migration, a special issue of the JSE, seismic True Amplitudes edited by Martin Tygel. 2001 |
| [17] | 刘文卿. 提高地震速度场精度的一种方法. 石油地球物理勘探 , 2002, 37: 176–178. Liu W Q. A method for improving the accuracy of seismic velocity. Oil Geophysical Prospecting (in Chinese) , 2002, 37: 176-178. |
| [18] | 徐升, GillesLambaré. 复杂介质下保真振幅Kirchhoff深度偏移. 地球物理学报 , 2006, 49(5): 1431–1444. Xu S, Gilles Lambaré. True amplitude Kirchhoff pre-stack depth migration in complex media. Chinese J.Geophys. (in Chinese) , 2006, 49(5): 1431-1444. |
| [19] | 刘守伟, 程玖兵, 王华忠, 等. 偏移距域/角度域共成像点道集与偏移速度的关系. 地球科学-中国地质大学学报 , 2007, 32(4): 575–582. Liu S W, Cheng J B, Wang H Z. Relationships between offset domain/angle domain common image gathers and migration velocity. Earth Science-Journal of China University of Geosciences (in Chinese) , 2007, 32(4): 575-582. |
| [20] | Stolk C C, Symes. Kinematic artifacts in pre-stack depth migration. Geophysics , 2004, 69(2): 562-575. DOI:10.1190/1.1707076 |
| [21] | 刘洪, 刘红伟. Kirchhoff叠前时间偏移角度道集. 地球物理学报 , 2010, 53(5): 1207–1214. Liu H, Liu H W. Common-angle gathers based on Kirchhoff pre-stack time migration. Chinese J. Geophys. (in Chinese) , 2010, 53(5): 1207-1214. |
| [22] | 袁江华, 刘洪, 首皓, 等. 面向目标的叠前角度道集提取策略. 石油物探 , 2007, 46(4): 334–338. Yuan J H, Liu H, Shou H, et al. Extraction scheme for object-oriented prestack angle gathers. Geophysical Prospecting for Petroleum (in Chinese) , 2007, 46(4): 334-338. |
| [23] | 程玖兵, 王华忠, 马在田. 窄方位地震数据双平方根方程偏移方法探讨. 地球物理学报 , 2005, 48(2): 399–405. Cheng J B, Wang H Z, Ma Z T. Double square root equation migration methods of narrow azimuth seismic data. Chinese J.Geophys. (in Chinese) , 2005, 48(2): 399-405. |
 2010, Vol. 53
2010, Vol. 53