2. 海岛(礁)测绘技术国家测绘局重点实验室, 青岛 266510;
3. 中国科学院国家天文台, 北京 100012;
4. 国家测绘局卫星测绘应用中心, 北京 100830;
5. 台湾交通大学土木工程学系, 台湾新竹 300
2. Key Laboratory of Surveying and Mapping Technology on Island and Reef, SBSM, Qingdao 266510, China;
3. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China;
4. Satellite Surveying and Mapping Application Center, SBSM, Beijing 100830, China;
5. Department of Civil Engineering, National Chiao Tung University, Hsinchu 300, China
卫星测高在物理海洋学、大地测量学和地球物理学等领域得到了重要广泛应用[1~3].海洋流场是物理海洋的基础研究内容,卫星测高可以对海洋进行时间跨度和空间覆盖面大的观测,是估计海洋表面地转流速度的重要空基技术之一,但是单一卫星测高任务很难给出完整的中尺度时空海洋变化.
许多学者对利用卫星测高计算洋流速度进行了研究.通过模拟研究,Leeuwenburgh等分析了利用卫星测高计算地转流速度的精度[4],认为在湾流地区误差方差为信号方差的15%~25%,并建议TOPEX/Poseidon (T/P)和Jason-1的地面赤道轨迹间距应为0.75°,以利用平行轨迹法得到最佳的地转流速度,但实际T/P和Jason-1的赤道间距为1.42°[5].平行轨迹法利用轨迹间的SSH (Sea Surface Height)之差计算地转流速度,相邻轨迹间距越小,就会放大测量误差的影响,特别是轨道误差的影响; 间距越大,增加了洋流中尺度变化的采用误差. Hwang等利用T/P测高数据分析了南中国海流场,利用相对SSH格网法研究了南中国海海流和涡旋[6].利用卫星测高得到网格化的SSH数据计算地转流速度,需要高精度的海洋大地水准面模型,否则只能得到相对地转流速度[7, 8].Yuan等利用流量站实际观测和AVISO (Archivage,Validation et Interprétation des données des Satellites Océanographiques,卫星海洋数据获取、校准和解释中心)提供的测高数据研究了吕宋海峡海流变化[9].Zhang等利用KMSS04平均海面高模型及重力场模型CG01C和EGM96,采用格网法研究了表层地转流[10],但是CG01C和EGM96的精度和分辨率有待于提高,KMSS04没有顾及海平面的时变.假设卫星测高的各项误差之间不相关,且SSH是一个各向同性、均质、稳定的随机结果,Schlax等从理论上分析了测高仪器误差、轨道误差等对由卫星测高计算地转流速度的影响,认为由此计算的地转流速度的均方误差超过信号标准偏差的20%[11].因此,如何改善基于卫星测高的地转流速度解算结果是一个重要的研究内容.
交叉点是同一测高卫星的上升和下降地面轨迹的交点,或者不同测高卫星地面轨迹的交点.理论上在有限时间间隔内不同弧段测量的交叉点处平均海面高应当相等,但是由于卫星定轨、洋流、海面地形、地球物理因素等的影响,交叉点处平均海面高并不相等.Shum等讨论了利用交叉点方法进行测高卫星精密定轨和精化地球物理参数[12],并应用于ERS和T/P等测高卫星[13~15].
本文利用卫星测高交叉点法,根据具有重复轨道卫星得到的SSH,估计上升和下降轨迹交叉点的地转流速度.交叉点法适用于单一或者多颗测高卫星[11, 16].但是测高交叉点的空间分布与地转流吻合程度不同,同时经过同一交叉点的上升和下降轨迹还有一定的时间间隔,如T/P同一cycle的上升和下降轨迹时间间隔可达10d[6, 17, 18],这些都增加了由交叉点计算地转流速度的不确定性.根据海洋地转流平衡方程,本文给出了交叉点地转流速度计算公式,分析了其精度,并计算了T/P和Jason-1在中国台湾东部的交叉点处的黑潮流速.
2 海洋地转流平衡根据物理海洋学[19],任意海水质元受到重力g、压力梯度P、摩擦力f和Coriolis力C的作用.定义xyz坐标系:z轴沿铅垂线方向,背离地心为正; x轴指向东为正,y轴指向北为正,构成右手正交坐标系.因此,xy平面在质元的任意小的邻域内是一个重力等位面.在xyz中描述地转流速度,分别用u,v,w表示沿三个轴的速度分量.如果海流是水平流动,那么Rossby数就远远小于1,同时风力和其他摩擦力十分小,可以忽略不计它们的影响.因此,在水平面内,压力和Coriolis力就形成平衡,可得地转平衡方程
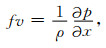
|
(1) |
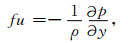
|
(2) |
式中,f=2Ωsinφ称为Coriolis参数,Ω为地球自转角速度,φ为纬度; p为压力; ρ=ρ(p,S,T)为海水密度,是压力p、盐度S和温度T的函数.满足地转方程(1)和(2)的海流称为地转流.海洋地转平衡中的力是很小的,一般都小于10-4N/kg,但也大于洋流的其他受力.压力梯度和Coriolis力决定了大部分洋流,世界上大部分主要洋流都近似满足地转平衡方程,如湾流、南极极地流、秘鲁流、黑潮、加利福利亚流等[8, 20].
对于地转流,在垂直方向,海洋近似为流体静力平衡[21],因此
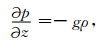
|
(3) |
根据地转平衡方程(1)和(2),地转流的表面速度主要决定于海面倾斜.因为海面倾斜,在水平面上就形成流体静力压力,产生水平压力梯度.设动力高度为ζ,海面倾斜在x和y方向的分量分别为ξ和η,则
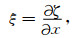
|
(4) |
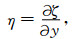
|
(5) |
代入式(1)和式(2),可得
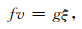
|
(6) |
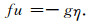
|
(7) |
卫星测高给出的SSH是海面和大地水准面之间的距离,SSH的变化不完全是地转流的贡献,也有地球物理的作用,如潮汐、大气压变化、温度的季节性变化等.为了计算地转流的速度,需要将地球物理影响从SSH中删除,这样就可以利用卫星测高结果计算地转流的速度.
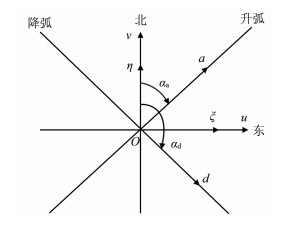
3 流速计算的交叉点公式由式(6)和式(7)可知,只要知道海面倾斜,就可以计算地转流的速度分量v和u.在卫星测高中,同一卫星的上升弧段和下降弧段以及不同卫星弧段的地面轨迹会产生交叉点.如图 1所示,以交叉点O为原点,建立xyz坐标系.根据卫星测高观测,可以计算沿上升弧段方位角αa和下降弧段方位角αd的海面倾斜ia和id.由图 1中的几何关系,可得
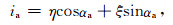
|
(8) |
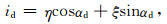
|
(9) |
|
图 1 测高卫星地面轨迹及交叉点 Fig. 1 Ground tracks and crossover point for altimetric satellite |
由式(8)和式(9)解得ξ和η,
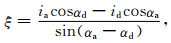
|
(10) |
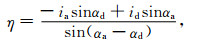
|
(11) |
代入式(6)和式(7),可得地转流速度v和u,
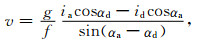
|
(12) |
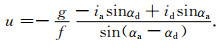
|
(13) |
海面倾斜是由卫星测高观测的海面高h和大地水准面起伏N通过数值微分得到的,即
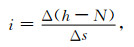
|
(14) |
式中,Δs为计算海面倾斜端点之间的水平距离.设海面倾斜的中误差为mi,距离中误差为ms,海面高中误差为mh,大地水准面起伏的中误差为mN,根据式(14),由误差传播定律[22]得
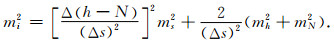
|
(15) |
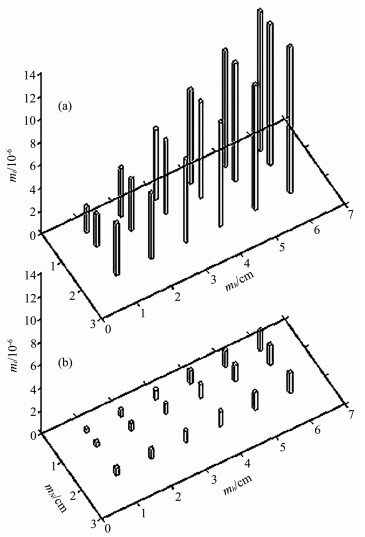
对于T/P的1 Hz的数据,相邻点之间的距离约7km,海面倾斜一般为10-7量级,因此可以忽略ms的影响.图 2给出了不同的Δs,mN和mh对应的海面倾斜精度.T/P,ERS-1/2和Jason-1等获得海面高的精度约为2~5cm[2, 23, 24].从图 2中可以看出,不但需要高分辨率、高精度的大地水准面模型,而且只有当Δs在50km以上,海面倾斜精度才有可能达到10-7量级.因此,必须对上升或者下降弧段的沿迹海面高进行滤波,滤波尺度一般应在50km以上.
|
图 2 不同海面高误差和大地高误差对应的海面倾斜误差 (a)Δs=7km; (b)Δs=50km. Fig. 2 Sea surface slope error derived from sea surface height error and geodetic height error |
设上升和下降弧段的海面倾斜为等精度mi,方位角计算也是等精度mα,根据误差传播定律,由式(12)和式(13)可得地转流速度分量v和u的精度mv和mu分别为
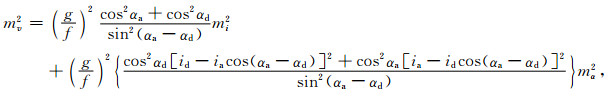
|
(16) |
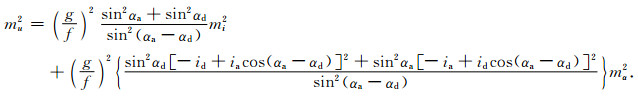
|
(17) |
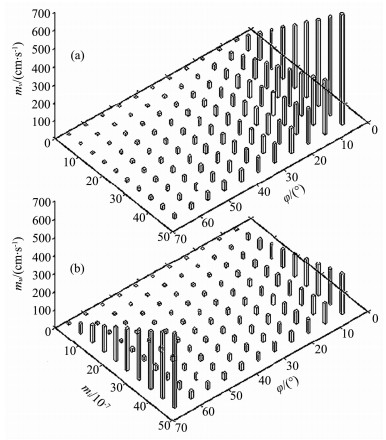
由于海面倾斜比较小,因此式(16)和式(17)中的右边第二项,即方位角计算精度的影响可以忽略不计.以T/P为例,图 3给出了不同纬度和不同海面倾斜精度下的mv和mu的结果比较.不同纬度地区海面倾斜对v和u精度的影响不同.纬度越低,海面倾斜误差对v的影响越大; 高纬度地区,轨迹方向接近东西向,海面倾斜误差的影响越来越小.纬度越低和接近卫星轨道倾角,海面倾斜误差对u的影响越大,特别是接近卫星轨道倾角,对u精度影响突然增大,在中纬度地区,海面倾斜误差对u的影响较小.海面倾斜精度越差,计算的地转流速度南北和东西分量的精度越差.只有当海面倾斜的精度达到10-7时,才有可能得到精度优于10cm/s的地转流速度.
|
图 3 以T/P为例,不同纬度和不同海面倾斜精度对应的地转流速度计算精度 (a)v; (b)u. Fig. 3 Geostrophic velocity accuracy due to latitude and sea surface slope |
黑潮是世界海洋中第二大暖流,是著名北太平洋副热带总环流系统中的西部边界流.黑潮由北赤道发源,经菲律宾,紧贴中国台湾东部进入东海,然后经琉球群岛,沿日本列岛的南部流去.在台湾东部海域,黑潮的流宽达200多公里,厚度达500多米,如图 4所示.

|
图 4 中国台湾周边平均洋流流速 (http://www.ncor.ntu.edu.tw) Fig. 4 Mean ocean current velocities around Taiwan, China |
本文采用T/P和Jason-1测高数据.T/P卫星是由美国NASA (National Aeronautics and Space Administration,美国国家宇航局)与法国CNES (Centre National d′Etudes Spatiales,法国空间局)联合的海洋地形试验卫星[25],于1992年8月10日发射升空,在海洋学、大地测量学和地球物理学等领域得到了广泛的应用[1].Jason-1是T/P的后继卫星[5],于2001年12月7日发射.在Jason-1初期,Jason-1和T/P处于同一个轨道,采用一前一后方式飞行,进行Jason-1测高计的检校,之后T/P偏移原来轨道,两个卫星并行飞行,使得两个卫星地面相邻轨迹赤道间距约为1.42°,这样就扩大了卫星观测,增加了更多的交叉点.
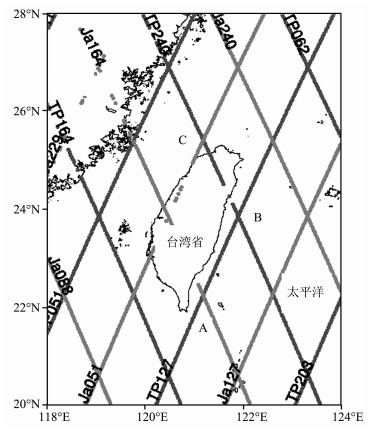
图 5给出了中国台湾东部海域T/P和Jason-1的地面轨迹,在台湾东部黑潮经过之地,有交叉点A和B,在台湾西北处有交叉点C.A是T/P的上升弧段(Pass127)和Jason-1的下降弧段(Pass164)的交点,处于黑潮的边缘.B是T/P的上升弧段(Pass 127)和下降弧段(Pass 240)的交点,处于黑潮流动轴线上.C是Jason-1的上升弧段(Pass51)和T/P的下降弧段(Pass240)的交点,位于台湾北部海域,距离黑潮较远.对照图 4和图 5,发现T/P的地面轨迹Pass127与黑潮的流向基本一致.本文利用2002~2005年的T/P (Cycle367-480)和Jason-1(Cycle24-137)的GDRs (Geophysical Data Records),进行地球物理和环境改正,计算沿轨迹海面高.对靠近陆地的测高数据应进行波形重定以改善测高数据质量[26, 27],这里C点距离陆地最近(31km),A和B距离陆地都在40km以上,因此直接使用GDRs.沿轨迹海面高包含有高频误差,采用Gauss滤波进行数据平滑,滤波窗口大小影响滤波作用,如果窗口过大,会产生数据失真,如果窗口太小,对原来观测起不到滤波作用[28].结合前面的分析,本文Gauss滤波窗口为50km.然后,利用卫星测高数据和中国台湾最新大地水准面模型计算A,B,C三点的动力高.该大地水准面模型是集成地面重力测量、船测重力、航空重力、卫星测高和数字地形等多源数据,使用最小二乘配置法计算的高精度模型,经过GPS/水准修正后,大地水准面起伏标准差优于5cm的精度[29].最后,根据公式(12)和(13)计算交叉点A、B和C处的地转流速度.
|
图 5 中国台湾周边T/P和Jason-1(Ja)地面轨迹分布和交叉点(图中的数字表示地面轨迹的Pass) Fig. 5 Ground tracks and crossover points of T/P and Jason-1 around Taiwan, China |
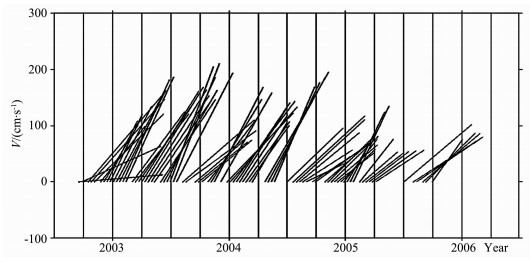
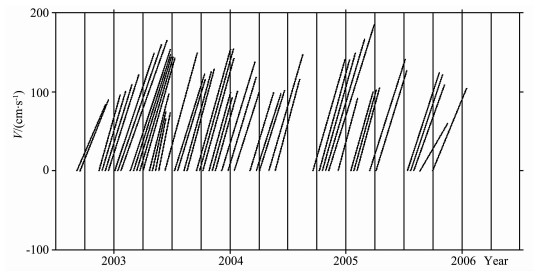
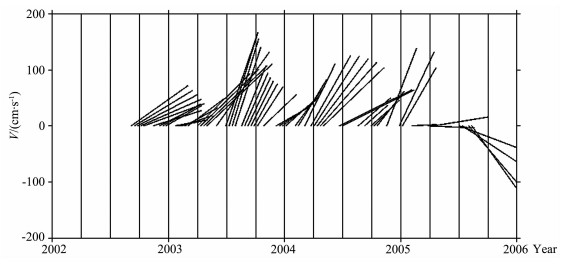
由于雷达测距、卫星定轨、地球物理改正、潮汐、交叉点的时空间隔等影响,由T/P和Jason-1测高数据计算的交叉点地转流速度包含诸多误差.因为T/P和Jason-1重复周期为10d,因此交叉点处地转流流速时间间隔为10d,而我们关心的是年均流速.因此为了消除高频误差影响,采用Gauss滤波器对流速序列进行滤波,滤波尺度为1a.这样就得到在三个交叉点A、B和C上的流速,如图 6~8所示.由于缺失卫星的一些Pass数据或者交叉点附近的GDRs,因此在图 6~8中就有一些时间没有数据.
|
图 6 交叉点A处的流速 Fig. 6 Current velocity at crossover point A |
|
图 7 交叉点B处的流速 Fig. 7 Current velocity at crossover point B |
|
图 8 交叉点C处的流速 Fig. 8 Current velocity at crossover point C |
在交叉点A处,平均流速为133cm/s,流向为30.57°.在B处,平均流速为127cm/s,流向为17.09°.在C处,平均流速为82cm/s,流向为62°.对照图 4和图 5,发现本文计算结果与中国台湾NCOR的结果基本吻合.
在这三个交叉点中,B处的流向最为稳定,其次为A处的流向,最差的是C处的流向,这主要是B处于黑潮轴线上,A位于黑潮的边缘,而C远离黑潮.同时,交叉点C距离陆地最近(只有31km),海深最浅(只有79m),因此C处的潮汐影响较大,潮汐模型精度最差,这样C处的测高数据精度就不如A和B.从图 6~8可以看,三个交叉点处的地转流存在周年变化.由于采用的时间较短,无法确定可靠的周年变化规律.
5 结论测高卫星对海洋进行了高时空分辨率的观测,测高数据包含了丰富的海洋信息.根据地转流平衡方程,本文分析了计算海洋表面地转流速度的测高交叉点方法,这是利用交叉点信息和大地水准面模型计算流速的直接方法.通过该方法的不确定分析,认为海面倾斜精度在50km尺度上应达到10-7量级,才能满足地转流速度计算的要求.对中国台湾东部黑潮流场的T/P和Jason-1的三个交叉点进行了处理,计算的地转流速度与中国台湾NCOR的结果基本一致,越靠近黑潮的交叉点的流速计算结果吻合得越好.
致谢感谢AVISO提供卫星测高数据.
| [1] | Hwang C, Shum C K, Li J C. Satellite altimetry for geodesy, geophysics and oceanography. Proceedings of the International Workshop on Satellite Altimetry. Berlin:Springer-Verlag, 2003 |
| [2] | Fu L L, Cazenave A. Satellite Altimetry and Earth Sciences. San Diego: Academic Press, 2001 . |
| [3] | Guo J Y, Gao Y G, Hwang C W, et al. A multi-subwaveform parametric retracker of the radar satellite altimetric waveform and recovery of gravity anomalies over coastal oceans. Science China -Earth Sciences , 2010, 53(4): 610-616. DOI:10.1007/s11430-009-0171-3 |
| [4] | Leeuwenburgh O, Stammer D. Uncertainties in altimetry-based velocity estimates. J Geophys Res , 2002, 107(C10): 3175. DOI:10.1029/2001/JC000937 |
| [5] | AVISO, PODAAC. AVISO and PODAAC User Handbook:IGDR and GDR Jason Products. CNES and NASA, 2004 |
| [6] | Hwang C, Chen S A. Circulations and eddies over the South China Sea derived from TOPEX/Poseidon altimetry. J Geophys Res , 2000, 105(C10): 23943-23965. DOI:10.1029/2000JC900092 |
| [7] | Hwang C. A study of Kuroshio's seasonal variabilities using a gravimetric-altimetric geoid and TOPEX/Poseidon altimeter data. J Geophys Res , 1996, 101: 6313-6335. DOI:10.1029/95JC03800 |
| [8] | Colling A. Ocean Circulation. 2nd Edition. Oxford:Butterworth-Heinemann, 2001 |
| [9] | Yuan Y C, Liao G H, Wang H Q, et al. Variability of the currents in the Luzon Strait during spring of 2002 obtained from observations and satellite geostrophic currents and spectral analysis. Science in China Series D-Earth Sciences , 2009, 52(4): 519-531. DOI:10.1007/s11430-009-0041-z |
| [10] | Zhang Z Z, Lu Y, Hsu H T. Detecting surface geostrophic currents using wavelet filter from satellite geodesy. Science in China Series D-Earth Sciences , 2007, 50(6): 918-926. DOI:10.1007/s11430-007-0038-4 |
| [11] | Schlax M G, Chelton D B. The accuracies of crossover and parallel-track estimates of geostrophic velocity from TOPEX/Poseidon and Jason altimeter data. Journal of Atmospheric and Oceanic Technology , 2003, 20: 1196-1211. DOI:10.1175/1520-0426(2003)020<1196:TAOCAP>2.0.CO;2 |
| [12] | Shum C K, Zhang B H, Schutz B E, et al. Altimeter crossover methods for precision orbit determination and the mapping of geophysical parameters. Journal of the Astronautical Sciences , 1990, 38(3): 355-36. |
| [13] | Carnochan S, Moore P, Ehlers S. ERS-1 radial position refinement by dual crossover analysis with TOPEX/Poseidon. Adv Space Res , 1995, 16(12): 12119-12122. |
| [14] | Smith A J E, Hesper E T, Kuijper D C, et al. TOPEX/Poseidon orbit error assessment. Journal of Geodesy , 1996, 70(9): 546-553. DOI:10.1007/BF00867862 |
| [15] | Le Traon P-Y, Ogor F. ERS-1/2 orbit improvement using TOPEX/POSEIDON:the 2 cm challenge. J Geophys Res , 1998, 103(C4): 8045-8057. DOI:10.1029/97JC01917 |
| [16] | Stammer D, Dieterich C. Space-borne measurements of the time-dependent geostrophic ocean flow field. Journal of Atmospheric and Oceanic Technology , 1999, 16: 1198-1207. DOI:10.1175/1520-0426(1999)016<1198:SBMOTT>2.0.CO;2 |
| [17] | Parke M E, Stewart R L, Farless D L, et al. On the choice of orbits for an altimetric satellite to study ocean circulation and tides. J Geophys Res , 1987, 92: 11693-11707. DOI:10.1029/JC092iC11p11693 |
| [18] | Morrow R, Coleman R, Church J, et al. Surface eddy momentum flux and velocity variances in the southern ocean from Geosat altimetry. Journal of Physical Oceanography , 1994, 24(10): 2050-2071. DOI:10.1175/1520-0485(1994)024<2050:SEMFAV>2.0.CO;2 |
| [19] | Knauss J A. Introduction to Physical Oceanography. 2nd Edition. New Jersey: Prentice-Hall, . |
| [20] | Apel J R. Principles of Ocean Physics. London: Academic Press, 1990 . |
| [21] | Cushman-Roisin B. Introduction to Geophysical Fluid Dynamics. New Jersey: Prentice Hall, 1994 . |
| [22] | Guo J Y, Tao H X. Solution model of nonlinear integral adjustment including different kinds of observing data with different precisions. Trans Nonferrous Met Soc China , 2003, 13(3): 735-738. |
| [23] | Fu L L, Christensen E J, Yamarone C A, et al. TOPEX/Poseidon mission overview. J Geophys Res , 1994, 99(C12): 24369-24381. DOI:10.1029/94JC01761 |
| [24] | Martin S. An Introduction to Ocean Remote Sending. Cambridge: Cambridge University Press, 2004 . |
| [25] | AVISO. AVISO User Handbook:Merged TOPEX/Poseidon Products (GDR-Ms). CNES, 1996 |
| [26] | Guo J Y, Hwang C W, Chang X T, et al. Improved threshold retracker for satellite altimeter waveform retracking over coastal sea. Progress in Natural Science , 2006, 16(7): 732-738. DOI:10.1080/10020070612330061 |
| [27] | 郭金运, 高永刚, 常晓涛, 等. 近岸海域EnviSat卫星测高波形重定的Threshold优化算法. 地球物理学报 , 2010, 53(4): 807–814. Guo J Y, Gao Y G, Chang X T, et al. Optimal threshold algorithm of EnviSat waveform retracking over coastal sea. Chinese J Geophys (in Chinese) , 2010, 53(4): 807-814. |
| [28] | Guo J Y, Han Y B, Hwang C. Analysis on motion of earth's center of mass observed with CHAMP mission. Science in China Series G-Physics Mechanics and Astronomy , 2008, 51(10): 1597-1606. DOI:10.1007/s11433-008-0152-0 |
| [29] | Hwang C, Shih H C, Guo J Y, et al. Zonal and meridional ocean currents at TOPEX/Poseidon and JASON-1 crossovers around Taiwan:error analysis and limitation. Terrestrial, Atmospheric and Oceanic Sciences , 2008, 19(1-2): 151-162. DOI:10.3319/TAO.2008.19.1-2.151(SA) |
 2010, Vol. 53
2010, Vol. 53

