地球物理学报  2010, Vol. 53 Issue (11): 2574-2581   PDF    
引用本文
游为, 沈云中, 范东明 等. 基于卫星轨道扰动理论的重力反演算法. 地球物理学报, 2010, 53(11): 2574-2581, doi: 10.3969/j.issn.0001-5733.2010.11.005.  
You W, Shen Y Z, Fan D M, et al. The algorithm of Earth's gravitational field recovery based on satellite's orbital perturbation theory. Chinese J. Geophys. (in Chinese), 2010, 53(11): 2574-2581, doi: 10.3969/j.issn.0001-5733.2010.11.005.  
基于卫星轨道扰动理论的重力反演算法
游为1 , 沈云中2 , 范东明1 , 冉将军3     
1. 西南交通大学测量系, 成都 610031;
2. 同济大学测量与国土信息工程系, 上海 200092;
3. 中国科学院测量与地球物理研究所, 武汉 430077
收稿日期 2010-03-12, 2010-05-22 收修定稿
基金项目: 国家自然科学基金(40474006, 40874016), 西南交通大学优秀博士论文培育项目(1003), 西南交通大学博士创新基金(09006)和同济大学土木学科访学基金(0901)资助
作者简介: 游为, 男, 1985年生, 西南交通大学博士研究生, 主要从事低轨重力卫星测量确定地球重力场模型的研究.E-mail:1985youwei@163.com
摘要: 为了更充分利用低轨重力卫星的高精度观测数据, 根据卫星轨道的扰动理论, 导出了应用卫星轨道与星间距离观测值联合反演地球重力场模型的算法.该算法的实质是将牛顿运动方程在卫星轨道处进行展开, 转化为第二类Volterra积分方程, 并采用基于移动窗口的9次多项式内插公式进行数值求解.给出了该算法的观测方程, 用QR分解法消去局部参数矩阵, 最后采用预条件共轭梯度法求解法方程.利用GRACE卫星2008-01-01~2008-08-01时间段内的轨道及星间距离观测数据, 解算了120阶次的地球重力场模型SWJTU-GRACE01S, 该模型在120阶处的阶方差为1.58×10-8, 大地水准面差距累计误差为22.29 cm, 与美国GPS水准网比较的标准差为0.793 m, 结果表明:SWJTU-GRACE01S模型精度介于EIGEN-GRACE01S与EIGEN-GRACE02S模型之间, 从而验证了该算法的有效性.
关键词: 卫星轨道扰动      地球重力场模型      牛顿运动方程      星间距离      多项式内插      QR分解     
The algorithm of Earth's gravitational field recovery based on satellite's orbital perturbation theory
YOU Wei1, SHEN Yun-Zhong2, FAN Dong-Ming1, RAN Jiang-Jun3     
1. Department of Surveying, Southwest Jiaotong University, Chengdu 610031, China;
2. Department of Surveying and Geomatics, Tongji University, Shanghai 200092, China;
3. Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China
Abstract: In order to make full use of precise observations of low orbital gravity satellites, the algorithm of Earth's gravitational field recovery by using the combined observations of satellite's orbits and inter-satellite's ranges has been presented based on satellite's orbital perturbation theory. The key point of this algorithm is to derive the linearized expression from Newton's nonlinear equation of motion by Taylor linear expansion on the measured orbits such as kinematical orbits as approximate values. The interpolation formula of shifted polynomial to degree 9 has been used to resolve the second Volterra integration equations. The observational equations related to the satellite's orbits and inter-satellite's ranges have been derived. The regional parameters are first eliminated by using QR decomposition, the global parameters are then solved by the preconditioned conjugate gradient approach. An Earth's gravitational field model up to degree and order 120 named SWJTU-GRACE01S has been resolved by using GRACE datum between 2008-01-01~2008-08-01. The degree variance and cumulative geoid height of the model are 1.58×10-8 and 22.29 cm respectively. The standard deviation of the model compared to GPS leveling networks of USA is 0.793 m. The results show that the precision of the model SWJTU-GRACE01S is between EIGEN-GRACE01S and EIGEN-GRACE02S up to the same degree and order..
Key words: Satellite's orbital perturbations      Earth's gravitational field model      Newton's equations of motion      Inter-satellite's ranges      Polynomial interpolation      QR decomposition     
1 引言

自2000年以来国内外学者基于低轨重力卫星观测数据，利用不同方法恢复了大量高精度、高分辨率的地球重力场模型，仅ICGEM (International Centre for Global Earth Models)公布的地球重力场模型就多达34个，确定这些模型所采用的方法包括:经典动力学法[1~5]、能量守恒法[6~11]、加速度法[12~15]、短弧长积分法[16, 17]及天体力学法[18].国际主要研究机构，如GFZ、CSR、JPL等，采用经典动力学法反演了EIGEN-及GGM-系列模型，但由于经典动力学法是基于卫星初始状态向量、先验地球重力场模型及其他力模型对非线性卫星运动方程进行线性化，不仅需要多次迭代计算，每次迭代都要重新进行轨道积分及变分方程积分计算，而且线性化误差随着积分弧段的延长而增大.能量守恒法是一种较简便的方法，其观测方程为线性方程，不需要先验地球重力场模型及卫星初始状态向量，但需要对卫星轨道进行数值微分得到速度，对于GRACE卫星来说，文献[10, 11]虽然采用了一些改进的方法，但观测方程依然包含有速度向量，不能完全由星间距离或距离变率来表示，故该方法的精度受到速度向量精度的影响，且能量守恒法主要与沿轨道方向的分量有关，而不能充分利用轨道垂直方向及径向分量的观测信息.加速度法可以充分利用三个方向的信息，但需要对卫星轨道进行二阶数值微分得到加速度，而微分运算大大降低了解算精度，文献[13~15]提出了平均加速度法，将相邻三个历元的轨道作为组合观测值来求解地球重力场模型，但是观测值定权比较复杂，且不能很好地利用星间距离或距离变率数据作为观测值来求解模型.短弧长积分法将牛顿运动方程转化为基于边值问题的数值积分方程，但由于力模型误差的累积限制了该方法积分弧长的延长.天体力学方法也是基于经典动力学方法，将卫星初始状态向量、位系数与动力学参数作为未知参数整体求解，不需要非保守力加速度计数据.文献[19]给出了基于卫星轨道和速度扰动的理论公式，但没有给出具体的数值计算公式与计算结果.

本文根据文献[19]的卫星轨道扰动理论，导出了基于卫星轨道及星间距离观测值联合解算地球重力场模型的数值计算方法.该算法将低轨卫星的轨道位置直接作为Taylor线性化的展开点，避免了线性化误差随轨道长度的积累，理论上适用于任意长弧段的观测数据解算，通过模拟及实测数据计算验证了该算法的有效性和可靠性.

2 基于扰动理论的轨道及星间距离观测方程

根据牛顿第二定律:

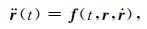
(1)

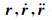
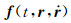
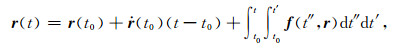
其中，分别为卫星在任意时刻的位置、速度及加速度向量，为t时刻卫星所受的作用力，包括中心引力、非球形引力、日月引力、固体潮、海潮、大气潮、极潮、相对论效应及非保守力等，非保守力可由低轨重力卫星的加速度计获得，而其他力模型的相关计算公式可参考文献[20].对式(1)二重积分得:

(2)

其中，t0为弧段初始历元.通过分部积分，将式(2)转化为一重积分公式:

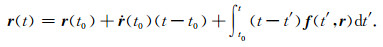
(3)

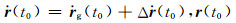
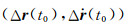
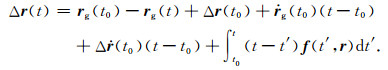
设任意时刻通过GPS测得的低轨重力卫星轨道位置向量为rg(t)，则r(t)=rg(t)+Δr(t); 在初始历元t0处，有:=rg(t0)+Δr(t0)，其中Δr(t)为t时刻卫星轨道的改正向量，为初始历元t0的卫星轨道状态向量改正值，代入式(3)得:

(4)

将f(t′，r)在该时刻t′的卫星轨道状态向量处Taylor线性展开得:

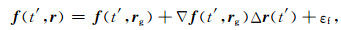
(5)

其中，∇f(t′，rg)为力模型的梯度张量，εf为力模型残差.将式(5)代入式(4)得:

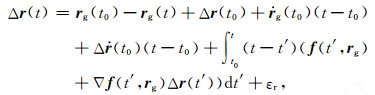
(6)

其中，εr为轨道向量残差，Δr(t′)可用式(7)进行回代:

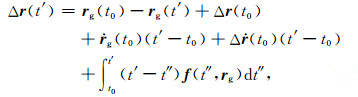
(7)

将式(7)代入式(6)中，得:

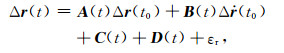
(8)

式(8)即为在某一历元处基于卫星轨道扰动的观测方程，其中:

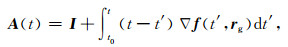
(8a)

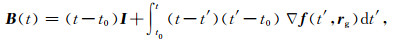
(8b)

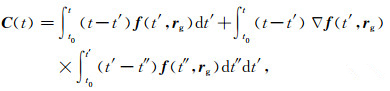
(8c)

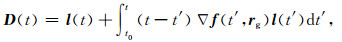
(8d)

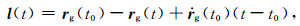
(8e)

其中，I为单位阵，A(t)、B(t)分别为初始轨道及初始速度改正向量的系数阵，C(t)中包含有全局未知参数的系数阵，D(t)为常数项.

对于GRACE类型的卫星，在某一历元处的星间距离ρ与卫星轨道存在如下关系式:

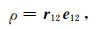
(9)

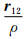
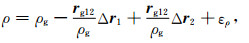
其中，r12=r2-r1为两颗卫星轨道向量之差，e12=为星间单位向量.将式(9)在卫星轨道处Taylor线性展开得:

(10)

其中，是利用卫星轨道所解算的星间距离，Δr1、Δr2分别为两颗卫星的轨道扰动向量，ερ为星间距离残差.将基于轨道扰动的观测方程式(8)代入式(10)，即得到基于星间距离的扰动公式.

3 数值积分和基于QR分解的局部参数消去法 3.1 基于移动窗口的多项式内插公式

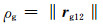
基于卫星轨道扰动的观测方程中包含对力函数的积分计算，而很多力函数无法求得解析解，且只已知了在观测历元处的数值.我们先将这些积分运算转化为每相邻两个历元的积分求和，再采用基于移动窗口的多项式内插公式内插出两相邻历元之间任意时刻的函数值，从而得到力函数在两相邻历元的积分值.(8)式中四个积分计算均可转化为如下积分运算:

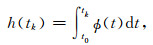
(11)

其中，Φ(t)为力模型或力梯度模型的函数.式(11)可转化为如下相邻历元积分累加:

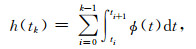
(12)

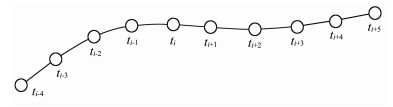
其中，[ti，ti+1]历元间的函数Φ(t)可根据相邻历元的函数值采用多项式公式内插，如图 1所示，若已知了相邻10个历元[ti-4，ti+5]的函数值，可采用9次多项式内插公式，如式(13)所示.

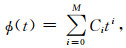
(13)

图 1 多项式内插 Fig. 1 Polynomial interpolation

其中，M=9为多项式次数，Ci为内插系数，可根据相邻10个历元的函数值采用式(14)求解:

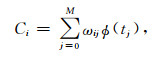
(14)

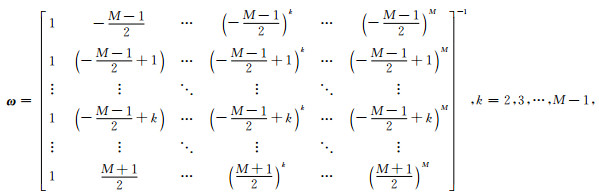
(15)

其中，ωij为ω矩阵的第i行第j列的元素.将式(14)代入式(13)得式(16)，采用式(16)就可计算[ti，ti+1]历元间的函数值，并将式(16)代入式(12)中即可进行积分运算.同理，若要计算[ti+1，ti+2]的多项式内插公式，可将内插窗口移动到[ti-3，ti+6]，利用该时间段的10个历元进行内插，这样可保证每次内插的时间段都在这10个离散历元的中间段，提高内插精度.

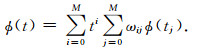
(16)

3.2 数值积分公式

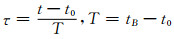
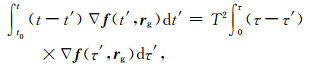
采用上述方法分别对轨道扰动方程的四个矩阵进行求解，令，其中，T为整个弧段长度，tB为弧段结束历元.对A(t)中的积分式子进行如下变换:

(17)

再令，则τ′=τi+ηΔτ，其中N为某一弧段所有观测历元的个数，代入式(17)并通过变量替换得:

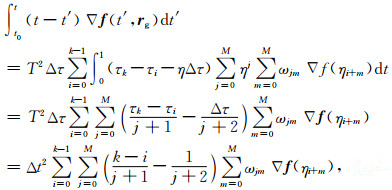
(18)

其中，Δt为两相邻历元间隔，将式(18)代入A(t)的计算中，可得:

(19)

同理，B(t)可化为:

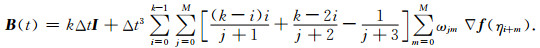
(20)

运用同样方法对C(t)中的两个积分分别计算得:

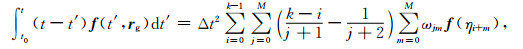
(21)

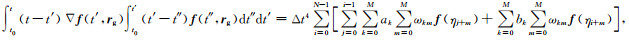
(22)

其中:

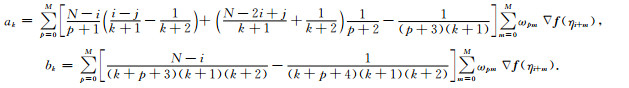
(23)

将式(21)、(22)、(23)代入式(8c)即可计算C(t).同理，再对D(t)积分可得:

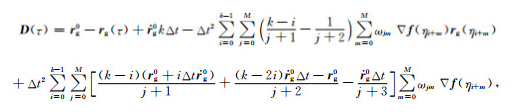
(24)

其中，rg0与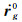分别为初始历元卫星轨道的位置与速度向量.

3.3 基于QR分解的局部参数消去法

基于式(8)与式(10)即可建立卫星轨道及星间距离观测值联合计算地球重力场模型的观测方程，从而可得到某一弧段的误差方程:

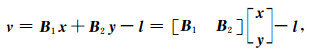
(25)

其中，v为观测值改正数向量，x为全局未知参数，即位系数向量，y为局部未知参数，包括初始状态向量等，B1、B2分别为全局未知参数及局部未知参数的系数阵，l为常数项.利用最小二乘原理求解该误差方程，得到法方程如式(26)所示:

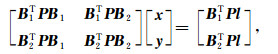
(26)

由式(26)可分别求解局部未知参数y和位系数向量x，如式(27)、(28)所示.

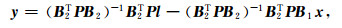
(27)

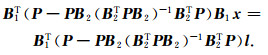
(28)

由于权阵P为对角矩阵，故可令P=(P1/2)TP1/2及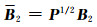，代入式(28)得:

(29)

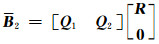
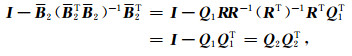
对矩阵珚B2进行QR分解得:，所以有

(30)

将式(30)代入式(29)得:

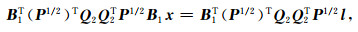
(31)

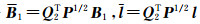
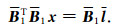
令，可将式(31)转化为式(32):

(32)

利用式(32)将各个弧段的法方程累加，即可消去局部系数阵，求解位系数向量x.由于星间距离主要与卫星间的相对位置向量有关，而与各个卫星绝对位置向量的关系很弱，所以局部系数阵B2是病态的，模拟数据表明矩阵B2的法方程条件数cond (B2T PB2)＞107，呈现严重病态性，直接对其求逆将得不到稳定的结果，而矩阵珚B2的条件数cond (B2)≈103，对其QR分解能得到相对稳定且精确得多的结果，因而QR分解法避免了对局部系数阵的直接求逆，能降低由于局部系数阵病态而导致位系数向量解算结果的不稳定.

4 基于卫星轨道及星间距离观测值联合反演的模拟与分析

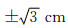
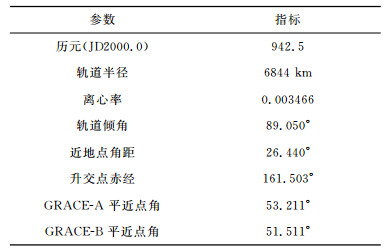
考虑到单独利用星间距离观测值解算重力场模型时，局部法方程矩阵的病态性太强，将卫星轨道及星间距离扰动联合解算重力场模型时，可降低法方程矩阵的病态性.两种观测值联合解算地球重力场模型的关键在于权的确定，由于卫星轨道扰动更能反映地球重力场的长波信息，而星间距离扰动更能反映地球重力场的短波信息，若星间距离观测值的权定的大些，则地球重力场模型的中高阶位系数更能准确地解算，若轨道观测值的权定的大些，则地球重力场模型的低阶位系数更能准确地解算，因此权阵的确定直接影响到求解的位系数精度.采用方差分量估计能对不同类观测值进行合理定权，但计算时需要多次迭代，而高阶地球重力场模型的求解本身非常耗时，因此本文采用方差分量估计迭代定权显得并不现实.若按照先验精度信息定权，假设轨道位置精度为±3cm，星间距离精度为±10μm，令先验单位权中误差为轨道位置在某一方向上的精度，则轨道位置各方向观测值的权为1，星间距离观测值的权为3×106.由于星间距离误差方程中，还包括卫星轨道及保守力与非保守力模型，其误差的影响将导致星间距离本身的精度并不能完全体现出来，因此需要对星间距离观测值进行降权处理，根据Mayer-Gürr Torsten博士的建议和我们的模拟数据计算表明将星间距离观测值的权降为3× 104较合适.

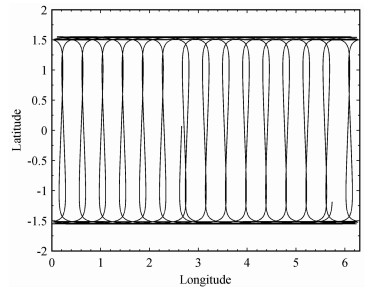
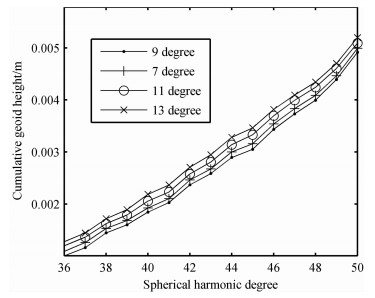
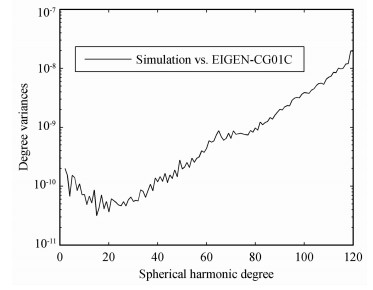
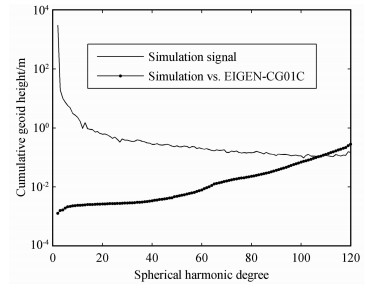
以EIGEN-CG01C作为参考重力场模型，GRACE卫星初始历元的轨道根数如表 1所示，采用8阶Runge-Kutta单步积分公式及12阶Adams、Cowell多步法隐式公式模拟GRACE卫星1个月的轨道及星间距离数据，历元间隔为10s，图 2为GRACE-A卫星在地固系下一天的模拟轨道，轨道位置及星间距离各加入±3cm和±10μm的随机误差.将模拟的轨道及星间距离作为观测数据，因作者的计算机难于用本文算法实施长弧段计算，每个弧段长度为0.5h，分别建立基于卫星轨道及星间距离扰动的观测方程，采用QR分解法消去局部参数矩阵，将位系数按以次为主的顺序排列，计算法方程的块对角矩阵，并将块对角矩阵的逆阵作为预条件矩阵，采用OSU91A模型作为预条件共轭梯度法的初值，利用预条件共轭梯度法求解法方程，解算得到对应的地球重力场模型.首先利用模拟的10天轨道及星间距离数据，分别采用不同次的多项式求解了四组50阶次的地球重力场模型，与参考重力场模型比较得到各模型的大地水准面差距累计误差(图 3)，比较可得采用9次多项式求解的模型精度最高，增加或减少多项式次数，重力场模型的精度都将降低.然后利用1个月的模拟轨道及星间距离数据解算了120阶次地球重力场模型，将该模型与EIGEN-CG01C模型比较，求解各阶位系数的阶方差(图 4)及大地水准面差距累计误差(图 5)，可知在顾及观测值误差的情况下，该模型在120阶次的阶方差为1.63×10-8，大地水准面差距累计误差仅为19.37cm，充分说明了本文方法的有效性.

图 2 GRACE-A卫星1天的模拟轨道 Fig. 2 Simulated orbits of GRACE-A satellite for one day
图 3 各阶多项式对应模型的大地水准面差距累计误差比较 Fig. 3 A comparison of cumulative geoid height between models of different polynomials
图 4 模拟重力场模型的阶方差 Fig. 4 Degree variances of simulated gravitational field model
图 5 模拟重力场模型的大地水准面差距累计误差 Fig. 5 Cumulative geoid height of simulated gravitational field model
表 1 GRACE卫星初始历元的轨道根数 Table 1 Initial orbital elements of GRACE
5 基于实测数据的重力场模型解算

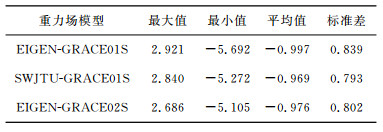
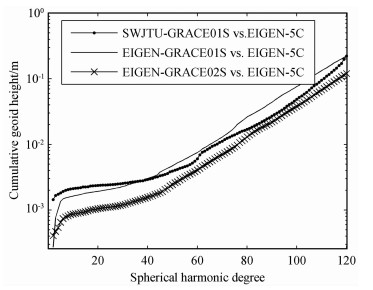
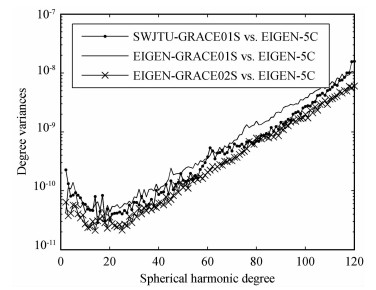
本文基于GRACE卫星2008-01-01~2008-08-01时间段内近200天的轨道及星间距离数据恢复了120阶次的地球重力场模型SWJTU-GRACE01S.首先对JPL所提供的GRACE卫星Level-1B数据预处理，得到重力场模型解算所需要的格式，然后计算卫星所受的各保守力大小，其中日月引力采用JPL所提供DE405星历表计算，固体潮、极潮和相对论效应都是基于IERS2003技术规范计算，海潮采用CSR3.0模型计算，大气和海洋的短期质量变化影响采用AOD1B RL04数据计算，非保守力由加速度计数据和姿态数据计算.基于本文方法，将位系数(14637个)作为全局未知参数，弧段初始状态向量(每个弧段6个)和加速度计各方向偏差(每个弧段3个，加速度计尺度采用JPL所提供的参考值)作为局部未知参数，以OSU91A模型作为初始重力场模型，因计算机原因各弧段长度为0.5h，卫星轨道与星间距离的权比仍然采用模拟数据计算的标准.先基于QR分解法消去各弧段的局部参数，然后将各弧段全局参数的法方程矩阵累加，采用预条件共轭梯度法，求解120阶次的地球重力场模型SWJTU-GRACE01S.计算工作在intel i5 750四核计算机上进行，主频为2.67G，内存为4G，共用约90h处理完200天GRACE实测数据.为分析SWJTU-GRACE01S的内符合精度，以GFZ高精度的EIGEN-5C模型为参考，求得SWJTU-GRACE01S的阶方差及大地水准面差距累计误差，并与EIGEN-GRACE01S及EIGEN-GRACE02S模型所对应的精度比较，结果如图 6，图 7所示.为了进一步对模型的外符合精度进行检验，选择美国的5379个GPS水准点的大地水准面差距作为基准，将该模型所解算的这些点的大地水准面差距与基准值进行比较，得到该模型的外符合精度(表 2).通过内外符合精度比较可得:SWJTU-GRACE01S模型在120阶处的阶方差为1.58×10-8，大地水准面差距累计误差为22.29cm，与美国GPS水准网比较的标准差为0.793m，结果表明该模型的精度高于EIGEN-GRACE01S模型而低于EIGEN-GRACE02S模型.需要说明的是，SWJTU-GRACE01S模型的低阶位系数精度低于EIGEN-GRACE01S模型，采用弧段较短应该是其重要原因.

图 6 三组模型的大地水准面差距累计误差比较 Fig. 6 A comparison of cumulative geoid height between three models
图 7 三组模型的阶方差比较 Fig. 7 A comparison of degree variances between three models
表 2 模型与美国实测GPS水准网的大地水准面差距比较(m) Table 2 A comparison of geoid height between three models and GPS leveling networks in USA (m)
6 结论

(1)采用基于移动窗口的多项式内插公式，可高精度实现基于轨道扰动观测方程中的数值积分计算，从而有效代替了经典动力学法的变分方程计算.

(2)采用QR分解法，可快速而方便地消去局部系数阵，并且避免了对局部法方程矩阵的直接求逆，能降低由于局部系数阵病态而导致的位系数解算结果不稳定.

(3)基于卫星轨道及星间距离观测值联合解算的方法能够有效利用GRACE卫星观测数据的高精度信息，确定出高精度地球重力场模型，本文所解算的模型在120阶处的阶方差为1.58×10-8，大地水准面差距累计误差为22.29cm，与美国GPS水准网比较的标准差为0.793 m，从而为应用实际低轨重力卫星观测数据确定地球重力场模型的解算提供了一种有效的方法.

致谢

感谢日本京都大学徐培亮博士及德国波恩大学Mayer-Gürr Torsten博士给予的帮助，感谢两位匿名审稿专家所提出的宝贵意见.

参考文献
[1] Visser P N A M, van den Ijssel J, Koop R, et al. Exploring gravity field determination from orbit perturbations of the European Gravity Mission GOCE. Journal of Geodesy , 2001, 75: 89-98. DOI:10.1007/s001900000155
[2] Arsov K, Pail R. Assessment of two methods for gravity field recovery from GOCE GPS-SST orbit solutions. Advances in Geosciences , 2003, 1: 121-126. DOI:10.5194/adgeo-1-121-2003
[3] Zhu S, Reigber C, König R. Integrated adjustment of CHAMP, GRACE and GPS data. Journal of Geodesy , 2004, 78: 103-108.
[4] Reigber C, Schmidt R, Flechtner F, et al. An earth gravity field model complete to degree and order 150 from GRACE:EIGEN-GRACE02S. Journal of Geodynamics , 2005, 39: 1-10. DOI:10.1016/j.jog.2004.07.001
[5] 张兴福, 沈云中, 胡雷鸣. 基于CHAMP短弧长动力学轨道的地球重力场模型. 地球物理学报 , 2007, 50(1): 106–110. Zhang X F, Shen Y Z, Hu L M. A gravity field model based on CHAMP short-arc dynamical orbits. Chinese J. Geophys (in Chinese) , 2007, 50(1): 106-110.
[6] Han S C. Efficient global gravity field determination from satellite-to-satellite tracking. Ohio:School of the Ohio State University, 2003
[7] Howe E, Stenseng L, Tscherning C C. Analysis of one month of CHAMP state vector and accelerometer data for the recovery of the gravity potential. Advances in Geosciences , 2003, 1: 1-4. DOI:10.5194/adgeo-1-1-2003
[8] Gerlach C, Sneeuw N, Visser P, et al. CHAMP gravity field recovery using the energy balance approach. Advances in Geosciences , 2003, 1: 73-80. DOI:10.5194/adgeo-1-73-2003
[9] Visser P, Sneeuw N, Gerlach C. Energy integral method for gravity field determination from satellite orbit coordinates. Journal of Geodesy , 2003, 77: 207-216. DOI:10.1007/s00190-003-0315-8
[10] 王正涛, 李建成, 姜卫平, 等. 基于GRACE卫星重力数据确定地球重力场模型WHU-GM-05. 地球物理学报 , 2008, 51(5): 1364–1371. Wang Z T, Li J C, Jiang W P, et al. Determination of earth gravity field model WHU-GM-05 using GRACE gravity data. Chinese J. Geophys (in Chinese) , 2008, 51(5): 1364-1371.
[11] 郑伟, 邵成刚, 罗俊, 等. 基于卫-卫跟踪观测技术利用能量守恒法恢复地球重力场的数值模拟研究. 地球物理学报 , 2006, 49(3): 712–717. Zheng W, Shao C G, Luo J, et al. Numerical simulation of Earth's gravitational field recovery from SST based on the energy conservation principle. Chinese J. Geophys (in Chinese) , 2006, 49(3): 712-717.
[12] 徐天河, 杨元喜. 利用CHAMP卫星几何法轨道恢复地球重力场模型. 地球物理学报 , 2005, 48(2): 288–293. Xu T H, Yang Y X. CHAMP gravity field recovery using kinematic orbits. Chinese J. Geophys (in Chinese) , 2005, 48(2): 288-293.
[13] Ditmar P, van Eck van der Sluijs A A. A technique for modeling the Earth's gravity field on the basis of satellite accelerations. Journal of Geodesy , 2004, 78: 12-33.
[14] Ditmar P, Kuznetsov V, van Eck van der Sluijs A A, et al. 'DEOS_CHAMP-01C_70':a model of the Earth's gravity field computed from accelerations of the CHAMP satellite. Journal of Geodesy , 2006, 79: 586-601. DOI:10.1007/s00190-005-0008-6
[15] Ditmar P, Liu X L. Dependence of the Earth's gravity model derived from satellite accelerations on a prior information. Journal of Geodynamics , 2007, 43: 189-199. DOI:10.1016/j.jog.2006.09.009
[16] Mayer-Gürr T, Ilk K H, Eicher A. ITG-CHAMP01:a CHAMP gravity field model from short kinematic arcs over a one-year observation period. Journal of Geodesy , 2005, 78: 462-480. DOI:10.1007/s00190-004-0413-2
[17] Mayer-Gürr T. Gravitationsfeldbestimmung aus der Analyse kurzer Bahnboegen am Beispiel der Satellitenmissionen CHAMP und GRACE. Bonn:Institute fuer Theoretische Geodaesi der Universitaet Bonn, 2006
[18] Prange L. AIUB-CHAMP02S:The influence of GNSS model changes on gravity field recovery using spaceborne GPS. Advances in Space Research , 2010, 45: 215-224. DOI:10.1016/j.asr.2009.09.020
[19] Xu P. Position and velocity perturbations for the determination of geopotential from space geodetic measurements. Celestial Mech Dyn Astr , 2008, 100: 231-249. DOI:10.1007/s10569-008-9117-x
[20] Montenbruck O, Gill E. Satellite Orbits, Models, Methods and Applications. Heidelberg:Springer Verlag, 2000