2. 中国科学院研究生院, 北京 100049
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China
阻滞势分析器是利用带电栅网分析空间等离子体能量从而得到离子密度、离子成份、离子温度、离子法向速度的就位探测仪器.美国早在20世纪60年代便开始发展阻滞势分析器技术,并将其广泛应用于空间等离子体探测领域.如早期的Ogo系列卫星[1]、AE卫星[2],Viking火星探测器[3]、Pioneer金星探测器[4],近期的NPOESS5新一代气象卫星等,都采用了阻滞势分析器及相关的探测技术.国外其他卫星的阻滞势分析器技术基本上都是由此发展而来.半个世纪以来,阻滞势分析器在国际上已经成为空间等离子体尤其是电离层等离子体就位探测的重要手段.遗憾的是,国内此项技术发展较晚,始终还没有此类仪器上天执行过探测任务.这一现状明显滞后于空间科学的发展需求.我们在实验室已有的技术基础上,针对500 km轨道高度的电离层环境研制了两台不同结构的阻滞势分析器,并做了详细的仿真分析和性能比较.
由于阻滞势分析器探测对象的能量很低,为eV量级,这个能量段的地面离子源很难保持稳定,阻滞势分析器的严格地面定标在国际上始终是一个难题.因此,利用计算机仿真程序对仪器特性进行分析,在优化仪器设计以及后期数据校正方面都具有十分重要的意义.另外,由于早期国际上并未充分利用仿真对阻滞势分析器数据做出校正,因此这些工作对以往探测数据的评估也具有重要的参考价值.
影响阻滞势分析器探测误差的因素主要包括:栅网的电场畸变、栅网透过率的各向异性以及等离子体鞘层的进一步影响.Hanson等[6]于1972年最早研究了栅网的有效偏压并给出了表达式,长期以来一直被广泛应用.Chao等[7, 8]于2000、2003年最早利用仿真程序研究了网格排列及电场畸变对离子运动的重要影响,并分析了这些因素引起的离子温度和离子法向速度的探测误差.Klenzing等[9, 10]随后于2008、2009年也利用仿真程序,对这些现象做了更加深入、微观的研究,分析了不同栅网模型对探测结果的影响.
在前人的仿真分析中,或者忽略了等离子体鞘层的影响,或者将阻滞栅网以外的栅网理想化处理,并且都没有分析离子密度的探测误差.本文利用粒子轨迹仿真软件全面研究了以上因素对仪器的影响,将所有栅网按照真实尺寸进行建模,首先分析了栅网透过率随离子能量和方向的改变,随后重点研究了等离子体鞘层带来的影响,最后根据仿真得到的伏安曲线进行密度、温度和速度三个参量的同时拟合,对仪器性能做了更加接近真实情况的仿真分析.这些工作对仪器的设计改进、实验测试和数据分析等有很好的指导意义.
2 阻滞势分析器工作原理阻滞势分析器主要用来测量离子的密度、温度、成份以及法向的整体移动速度.星载阻滞势分析器利用卫星的三轴稳定,传感器安装于卫星的迎风面,探测窗口始终保持向前.在卫星坐标系下,假设空间等离子体符合漂移麦克斯韦速度分布,漂移速度以卫星速度Vs占主导.图 1为结构最简单的一种阻滞势分析器.栅网G2加扫描偏压,一般为0~20 V,离子从探测窗口进入后被偏压抑制.当偏压为零时,所有离子都能通过G2;而当偏压为20 V时,几乎所有离子都会被阻挡(辐射带高能粒子的电流贡献远小于电离层热等离子体电流,可以忽略不计).随着偏压的扫描,只有高于阻滞能量的离子能到达收集极,使收集极上的电流随阻滞偏压变化,从而得到伏安特性曲线.通过分析伏安特性曲线,即可得到相关的离子参数.G1接卫星地,避免G2扫描偏压对环境等离子体的干扰.G3相对卫星地加一12 V固定偏压,抑制电子的进入,同时也防止收集极上二次电子和光电子的发射.G3的另一个作用是防止扫描偏压对前端电子学的干扰.以传感器法向向内为正x方向,收集极上接收到的第s种离子的电流为:
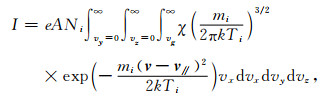
|
(1) |
|
图 1 阻滞势分析器原理图 Fig. 1 Principles of retarding potential analyzer |
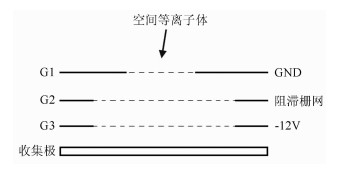
其中e为单位电荷,A为传感器开口面积,Ni为第i种离子的密度,mi是第i种离子的质量,k为玻尔兹曼常数,Ti为第i种离子的温度,v//为离子相对卫星的整体移动速度,χ为栅网透过率. 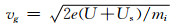
通常,处理阻滞势分析器数据时采用理想化模型,即假设栅网的透过率各向同性; 同时假设栅网对离子能量具有完美的选择性,即能量低于栅网偏压的离子全部被抑制,而能量高于偏压的离子完全按照栅网正面的透过率通过.此时,电流表达式可以简化为一维:
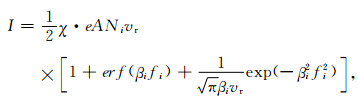
|
(2) |
其中Vr为离子整体的法向移动速度,以卫星速度Vs占主导. 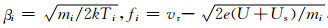
长期以来,这一简化结果被广泛应用于阻滞势分析器的数据处理中[11, 12].事实上,真实栅网的非理想性使上面的简化处理引人了不可忽视的探测误差.比如,栅网所在平面并不能保证完美的等电位,电场畸变使网孔中心的电位偏低,从而使能量低于阻滞偏压的离子也能穿过栅网.这一效果使伏安特性曲线趋于平缓,从而过高地估计等离子体的温度和漂移速度.另外,网孔处的电场畸变,使离子横向受力,从而使离子的运动轨迹变的复杂.尤其在多层栅网的情况下,不同能量的离子轨迹改变程度不同,在随后的栅网处就会表现出不同的透过率.又如,栅网的透过率各向异性,使多层栅网的总透过率与栅网排列方式密切相关等等.
所有这些因素最终都会体现在探测数据上,使探测结果偏离真实值.为了更好地了解仪器特性,必须全面分析这些因素对探测结果的影响程度.
3 仿真条件对阻滞势分析器的仿真利用粒子轨迹模拟软件SIMION7.0进行.仿真过程中,我们建立了四种栅网模型:
模型A:如图 1所示,共三层栅网,栅网之间等间距,每层栅网的尺寸相同,网孔为方形,透过率均为82.6%.
模型B:在模型A的基础上,将G2改为双层,共四层栅网,栅网等间距且间距与模型A一致,其他参数相同.
模型C:在模型A的基础上,将栅网间距改为1.75倍,其他参数相同.
模型D:在模型C的基础上,将网孔改为正六边形,其他参数相同.
其中,模型A、C、D的单层阻滞栅网结构在早期的阻滞势分析器中比较常见.模型C将栅网间距增大从而减小栅网间的电场,可以在一定程度上减弱电场畸变.模型D是考虑到电场均匀性和力学性能后,对模型C的进一步改进.模型B的双阻滞栅网结构在近些年比较常见,可以更好地保证阻滞电势的一致性,20世纪90年代以后随卫星上天的阻滞势分析器基本都采用了这种结构.
模型中所有的栅网都按照实际尺寸建立.在yz方向上栅网无限延伸,即忽略了粒子撞击仪器内壁造成的损失,这一点可以通过合理设计仪器的视场角来实现.每个模型中,所有栅网的网孔都沿x方向保持对齐,这在实际安装中可以通过定位孔来实现.在500 km轨道高度的电离层环境,离子的平均自由程远大于仪器的尺寸,故离子间的相互作用被忽略.另外,此轨道处的离子拉莫尔回旋半径远大于仪器尺寸而回旋频率低于等离子体频率,故可以忽略地磁场的影响. 500 km轨道高度处的德拜半径约为毫米量级,我们在每个模型前端5 mm处设置一个零电位界面用以模拟等离子体鞘层边界.而由于网孔的尺寸小于德拜半径,故可以认为所有电子都被G3排斥,仿真中不考虑电子的电流贡献.离子在撞击到栅网网丝上以后则认为其电荷被吸收,由于离子的能量较低,故不考虑溅射作用.另外,由于500 km轨道高度处离子的主要成份为O+,仿真中只考虑了O+一种离子进行计算.
在离子透过率的仿真中,阻滞栅网G2加5V固定偏压,将卫星电位Φs设为0V.每次人射1000个O+离子(仿真中发现,如果增加人射离子总数,透过率曲线的变化并不明显),人射位置在每一个模型前一个网孔对应的范围内随机分布.对每次人射的O+离子赋予相同的人射能量和人射俯仰角θ (不考虑方位角的影响,每次人射均设为零),利用蒙特卡洛方法,统计到达收集极的离子数.多次人射离子并改变每次的人射能量和人射角度,从而得到不同情况下的离子透过率.
在500 km轨道高度,由于等离子体中电子和离子热速度的不同,会使卫星相对等离子体带一定程度的负电,并在卫星表面形成等离子体鞘层.对于科学小卫星,这一电位通常为负几伏.在研究等离子体鞘层带来的影响时,将卫星电位Φs分别设为0 V和-2 V,首先分析了两种情况下透过率曲线的变化,随后在两种卫星电位时分别生成伏安特性曲线并进行参数拟合,分析等离子体鞘层对探测结果的影响.
最后,仿真中引入等离子体鞘层进一步分析不同状态下仪器的误差情况.我们研究了离子温度为500、1000、1500、2000、2500 K和3000 K时不同模型的伏安曲线响应,并通过最小二乘拟合给出不同模型不同温度输入时离子密度、温度和法向速度的探测误差.
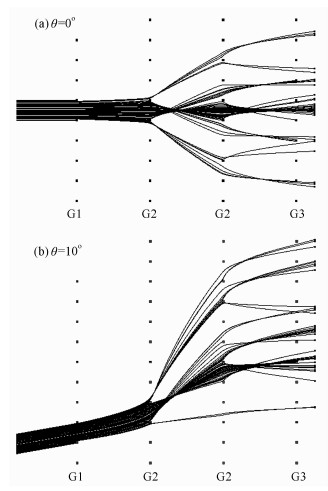
在生成伏安曲线的过程中,阻滞势从0 V到10 V变化,步长0.4 V.分别在不同的阻滞偏压下入射5000个离子,离子入射位置在每一个模型前端一个网孔对应的范围内随机分布.入射离子的定义完全参照空间中的真实情况,每次注入的离子速度在yz方向符合麦克斯韦分布,而在x方向符合以下分布,以模拟单位时间到达传感器开口处的离子:
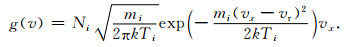
|
(3) |
在不同阻滞偏压下统计离子透过率作为归一化电流,从而得到伏安特性曲线.
4 离子透过率的仿真分析将阻滞栅网G2加5V固定偏压,分析不同能量、不同方向的离子透过率.按照前一章所述的仿真方法,我们分析了入射角θ为0°和10°两种情况,离子的x方向入射能量从4eV至7eV逐渐变化,如图 2, 其中每个数据点代表一次离子入射统计. Klenzing等的文章[9, 10]中报道了类似的工作.我们在这里扩展前人的思路,针对多种栅网模型进行了分析,同时也为后续章节的研究提供参考.
|
图 2 不同入射角时,不同模型粒子透过率随能量的变化 Fig. 2 Transparency of grids for particles with different ram energy and angle |
图 2中的阶梯函数代表理想栅网的透过率.其中统计透过率为每层栅网透过率的乘积.最大透过率为所有栅网网孔对齐时正面的光学透过率,即单层网透过率.可以想象,当离子能量远远高于阻滞能量时,将按照入射方向的光学透过率穿过栅网.
图 2a中θ=0°,当离子能量低于5eV时,模型A对离子的选择性最差,大量低于阻滞能量的离子都可以穿过栅网,比如离子能量为4.5eV时,仍有34%的透过率; 双层G2的模型B对离子的选择性最佳,低于5eV的离子透过率十分接近理想的阶梯函数; 莫型C与模型D对离子的选择能力介于中间,这是因为与模型A相比,G3距离G2较远,两者间电场较小,从而使G2处的电场畸变效果减弱; 其中,模型D略好于模型C,这是由于正六边形网孔的电场一致性优于方孔所致.当离子能量高于5eV时,透过率变化较为复杂.首先,对于模型A、模型C和模型D,当离子能量略高于阻滞偏压时,透过率会出现一极大值,这是由于电场畸变使本该撞击到网丝上的离子转向,从而绕过网丝; 這着离子能量继续升高,电场畸变不足以改变离子运动轨迹使其绕过网丝,从而使能量更高的离子透过率逐渐减小并趋于稳定.模型B比较特殊,由于栅网层数增多带来的复杂性,被电场畸变转向从而绕过网丝的离子并不能保证到达收集极,反而有可能撞击到后续栅网上,所以在略高于5eV处并没有出现透过率极大值,而且更高能量处变化也比较复杂.
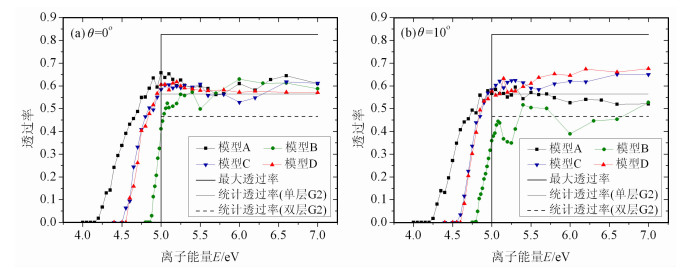
图 2b描述了θ=10°时的情况.与θ=0°相比,当离子能量低于5 eV时透过率基本没有变化.而当离子能量高于5 eV时,模型A、模型C、模型D的方向一致性明显好于模型B.模型B对离子入射方向十分敏感,与θ=0°时情况相比变化很大,在5. 2eV处透过率突然下降,之后随着能量升高波动也很剧烈.这可由多层栅网的网格排列来解释,如图 3b,当入射角θ=10°时,G2的第一层网首先挡住一部分离子,随后由于栅网的“聚焦”效果,大量离子撞击在G2第二层栅网的网丝上.这些现象很难通过理论推导给出,但通过仿真,可以给出比较直观的结果.
|
图 3 模型B离子x方向入射能量5.2eV时,不同入射角时的粒子轨迹 Fig. 3 Ions track for different ram angle in model B when ram energy is 5.2 eV |
由上面的分析可见,模型B的电场畸变相对较弱,对低能量离子的抑制效果较好,但多层栅网带来的复杂性使透过率的方向一致性较差.而模型D对低能量离子的抑制能力介于其他几个模型之间,且对高能量离子具有良好的方向一致性,另外,正六边形的网孔还具有较好的力学性能.据此,我们按照模型B和模型D制作了两种不同的阻滞势分析器.下面着重对这两个模型做出分析比较.
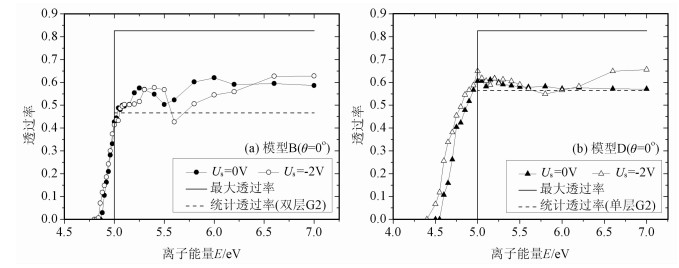
5 等离子体鞘层的影响仿真中,在每个模型前端5 mm处设置一个零电位界面用以模拟等离子体鞘层边界,则栅网G1相对环境等离子体的电位为Us,图 4中G2相对环境等离子体加5V偏压,G3相对Us的偏压为-12V,θ=0°其他仿真条件与第四节的相同.我们比较了卫星电位为0V和-2V时的情况.
|
图 4 模型B和模型D在卫星电位为0V和-2V时的透过率曲线(θ=0°) Fig. 4 Transparency for model B and D when the satellite potential is 0 V and -2 V (θ=0°) |
Chao等[7, 8]在文章中忽略了鞘层的影响; 而Klenzing等[10]虽然在2009年最新的报道中考虑了卫星电位,但由于其模型中将G1设为理想栅网,故只能模拟鞘层电场对离子到达G1前的加速,并不能体现对栅网电场畸变的作用.为了深入分析仪器性能,我们对鞘层影响做了接近真实情况的仿真.
由图 4a可知,模型B在不同的卫星电位时,对低于阻滞能量的离子始终保持了较好的抑制能力,十分接近理想栅网模型.而对于高于阻滞能量的离子,卫星电位为-2 V时,等离子体鞘层电场的影响使最外层栅网G1的电场畸变加剧,鞘层使栅网的“聚焦”能力增强.如图 5b,离子能量为5.6eV时,前两层栅网的“焦点”与Us=0V时相比更加靠前,离子通过焦点后发散,从而撞击到后续栅网上,造成透过率降低.随着离子能量继续升高,Us=-2V时的透过率逐渐增大并高于Us=0V时的,且两条曲线有交叉.这是因为随着离子能量的升高,“焦点”逐渐后移,从而使离子变为窄束穿过后面的网孔.
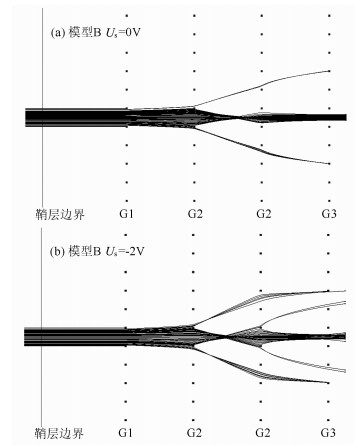
|
图 5 模型B在卫星电位为0 V和-2 V时的粒子轨迹(离子能量5.6 eV,θ=0°) Fig. 5 Ions track for model B when the satellite potential is 0 V and -2 V (ramenergy is 5.6 eV and θ=0°) |
Us=-2V时栅网的“聚焦”能力更强,从而使更高能量的离子具有较高的透过率.
模型D在卫星电位为-2 V时,对低于阻滞能量的离子抑制能力变差,如图 4b.这是因为当Us=-2V时,G3相对环境等离子体为-14V,这会加剧G2的电场畸变,从而允许更多的低能离子透过.能量较高于阻滞栅网的离子透过率变化不大,这与模型D的结构相对简单有关,不会因多层栅网的复杂性而损失过多的离子.随着离子能量的继续升高,Us=-2V时的透过率逐渐增大并高于Us=0V时的,这点与模型B相同.
图 6为2000 K时模型B在不同卫星电位时的伏安曲线响应,虚线和实线分别是卫星电位为0V和-2V时的拟合结果.参数输入中令vr等于卫星速度7600 m/s,忽略各个方向的离子漂移速度.由图 4a的分析可知,Us=-2V与Us=0V时相比,能量较高于阻滞偏压的离子透过率降低,能量更高(θ=0°时约为阻滞能量1.3倍以上)的离子透过率增大.另外,当离子能量远远高于阻滞偏压时,离子轨迹受电场“聚焦”作用的影响很小,不同卫星电位时的离子透过率都将接近光学透过率.500 km轨道处,卫星运动速度为7600 m/s,O+离子的能量集中在4.83eV左右.考虑到空间离子的能量分布,在扫描偏压的中间区域,尤其是中间偏低区域,卫星电位的降低将造成电流的过多收集; 而在偏压的最低端和最高端处,由于能量处于这些区域的离子数很少,故电流变化不大.这将使伏安曲线向右平移并变的陡峭,造成离子温度拟合结果的增大和离子法向速度拟合结果的减小.如图 6中,Us=0V时离子温度和离子法向速度的拟合结果分别为2160K和7642 m/s; 而Us=-2V时的拟合结果为2131K和7710m/s.
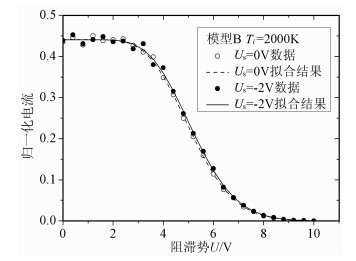
|
图 6 等离子体鞘层对伏安曲线的影响 Fig. 6 IU curve influenced by plasma sheath |
按照第三节的仿真条件,考虑到等离子体鞘层的影响,我们针对模型B和模型D分析伏安曲线以及反演参数的误差响应.在入射离子的定义中,我们令r等于卫星速度7600 m/s,卫星电位取-2V,忽略各个方向的离子漂移速度,离子温度分别取500、1000、1500、2000、2500K和3000K.
在前人的工作中,拟合曲线时都将收集电流按0V阻滞偏压时的电流归一化,从而忽略了对离子密度的分析.但事实上,离子密度是阻滞势分析器探测能力中的一个重要参量,也是电离层物理研究中的重要参量.离子密度的拟合还会间接影响到另外两个参数的拟合结果.为了更真实地反映仪器的性能,我们在研究中同时拟合密度、温度、速度三个参数,给出离子密度的相对误差及温度、速度的绝对误差.另外,我们在仿真生成伏安曲线时引入了等离子体鞘层的影响,从而能更全面地反应仪器的误差特性.
由图 7a可见,当温度很低时,离子基本沿正x方向入射,发散角很小,沿法线正面入射的离子透过率介于统计值和最大值之间,两个模型都收集到了比理论曲线高的电流.而由图 7b,温度较高时情况则相反,发散角较大使总的离子透过率低于理论值.电流的最大值与离子密度和离子法向速度有关,故实际曲线与理论曲线的偏移会影响这两个参数的拟合.模型D由于对低于阻滞能量的离子抑制能力较差,在图中表现出了曲线的水平偏移,这会引起离子法向速度的过高估计.伏安曲线中偏压的最低端电流有所起伏,这是因为阻滞偏压较低时,栅网G3的电场畸变对低能量离子作用较明显; 随着阻滞偏压的升高,能够穿过G2的离子能量越来越高,受G3的影响逐渐减小.
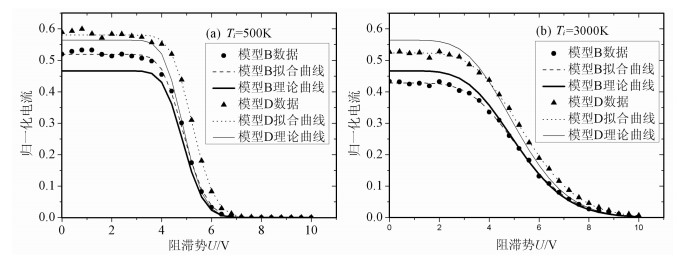
|
图 7 温度为500 K和3000 K时两种模型的伏安曲线 Fig. 7 IU curves for model B and D when the input temperature is 500 K and 3000 K |
具体的拟合结果如图 8所示.
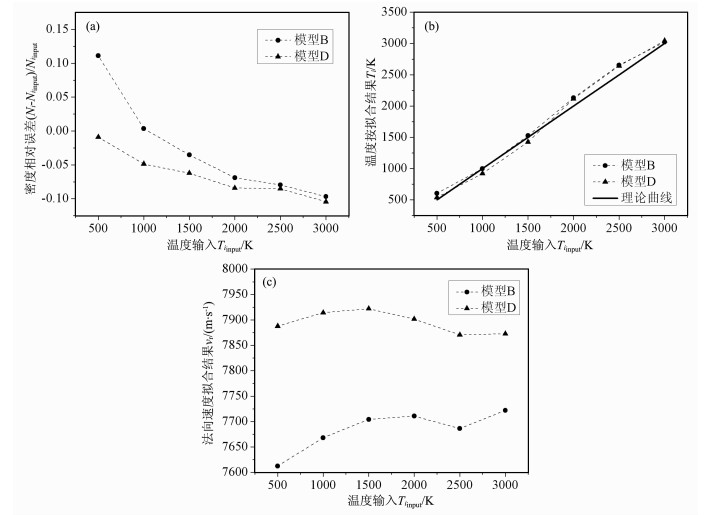
|
图 8 拟合参数密度(a)、温度(b)、和速度(c)随不同输入温度的变化 Fig. 8 Inferred parameters intention (a)、temperature (b) and velocity (c) varying different input temperature |
图 8a中,模型B的离子密度拟合对温度输入十分敏感,500 K时相对误差11%.随着温度升高误差逐渐转为负值,在3000 K时达到-9.7%,这是由发散角增大使离子透过率降低造成的.模型D的误差变化范围较小,但始终低于真实值.
离子温度的拟合结果较好,除了500 K时模型B的相对误差高达20.9%以外,其他各点两个模型的相对误差都小于10%.
两个模型的最大差别体现在离子法向速度的拟合中,如图 8c.模型B的最大拟合误差122 m/s, 出现在温度3000 K时,这一误差好于Chao等[8]的仿真结果180 m/s, 但比Klenzing等[9]的仿真结果60 m/s要差.可能的原因主要包括:栅网具体尺寸的差别带来的影响; 我们的仿真中考虑了等离子体鞘层以及由其引起的“聚焦”效应增强; 拟合伏安曲线时,我们按照真实的数据处理过程,同时拟合了离子密度、温度和法向速度三个参数,而不是像前人的研究中只拟合温度与法向速度,由此会带来一定的差别.
模型D的法向速度拟合结果较差,最大误差达到322 m/s,由此显示了真实栅网及等离子体鞘层对法向速度探测结果的严重影响.值得注意的是,模型D的误差变化范围相对较小,在不同温度时波动不大.
综合考虑以上结果,模型B在离子温度很小时,对离子密度和离子温度的探测误差较大,其他情况下表现出了较好的探测性能.模型D的误差对温度条件不敏感,对离子密度和离子温度的探测表现出很好的能力,但对离子法向速度的探测有较大的误差.
7 结论影响阻滞势分析器探测误差的因素主要包括栅网的电场畸变、栅网透过率的各向异性以及等离子体鞘层的进一步影响.文章针对真实栅网以及等离子鞘层对阻滞势分析器的误差影响进行了仿真分析,这些影响主要包括:
(1)低于阻滞能量的离子不能被完全抑制,部分会穿过栅网而到达收集极,使伏安曲线向右平移并趋于平缓,影响温度和法向速度的拟合结果;
(2)高于阻滞能量的离子会受到栅网的“聚焦”作用;
(3)等离子体鞘层电场会加剧栅网的“聚焦”作用,进一步影响离子运动,造成离子温度拟合结果偏低、法向速度拟合结果偏高;
(4)栅网对不同方向人射的离子透过率不一致,角度越大、温度越高的离子透过率越低;
(5)多层栅网的排列进一步影响离子的运动轨迹,离子每经过一层栅网后运动方向的改变使整体透过率更加复杂.
综上所述,离子的运动轨迹与离子能量、人射位置、人射方向、卫星电位、阻滞偏压、栅网排列等因素密切相关.以上这些因素综合作用于阻滞势分析器的探测结果,使伏安特性曲线与理论值之间产生偏离.我们在仿真分析中较为全面地考虑了以上因素,考察了500~3000 K温度时仪器的伏安曲线响应,通过最小二乘拟合分析离子密度、温度和法向速度的误差.对于双层阻滞栅网的结构(模型B),拟合结果随温度的变化较为剧烈,离子密度的相对误差为-9.7%~11%,离子温度的相对误差为-0.1%~20.9%;离子法向速度的误差为12.5~122 m/s.对于单层阻滞栅网的结构(模型D)离子密度的相对误差为-10.4%~0, 离子温度的相对误差为-5%~7.4%,离子法向速度的误差为272.6~322 m/s.
由于低能等离子体探测仪器在标定上存在困难,以上的仿真工作提供了一种详细了解仪器性能的方法.通过这些仿真分析,可以对仪器设计的进一步改进做出指导,也可为仪器在轨工作时的数据分析及修正提供参考依据.
下一步的工作主要包括建立详细的伏安曲线数据库,考察不同的温度、密度、漂移速度输人时阻滞势分析器的误差响应,从而满足日后数据分析和修正的需求.另外,还包括多种离子成份的分析以及非麦克斯韦分布下的误差分析等.
| [1] | Hanson W B, Sanatani S, Zuccaro D, et al. Plasma measurements with the retarding potential analyzer on Ogo6. J Geophys Res, Space Physics , 1970, 75(28): 5483-5501. DOI:10.1029/JA075i028p05483 |
| [2] | Hanson W B, Zuccaro D R, Lippincott C R, et al. The retarding potential analyzer on Atmosphere Explorer-C. Radio Sci , 1973, 8: 333. DOI:10.1029/RS008i004p00333 |
| [3] | Hanson W B, Sanatani S, Zuccaro D R. The Martian ionosphere as observed by the viking retarding potential analyzers. J Geophys Res , 1977, 82(28): 4351-4363. DOI:10.1029/JS082i028p04351 |
| [4] | Knudsen W C, Spenner K, Bakke J, et al. Pioneer venus orbiter planar retarding potential analyzer plasma experiment. IEEE Transactions on Geoscience and Remote Sensing , 1980, GE-18(1): 54-59. DOI:10.1109/TGRS.1980.350261 |
| [5] | Rich F J. Users guide for the topside ionospheric plasma monitor (SSIES, SSIES-2 and SSIES-3) on spacecraft of the Defense Meteorological Satellite Program. Air Force Phillips Laboratory, Hanscom AFB, MA , 1994, 1: 25. |
| [6] | Hanson W B, Frame D R, Midgley J E. Errors in retarding potential analyzers caused by nonuniformity of the grid-plane potential. J Geophys Res , 1972, 77: 1914-1922. DOI:10.1029/JA077i010p01914 |
| [7] | Chao C K, Su S -Y. Charged particle motion inside the retarding potential analyzer. Physics of Plasmas , 2000, 7(1): 101-107. DOI:10.1063/1.873817 |
| [8] | Chao C K, Su S -Y, Yeh H C. Grids effects on the derived ion temperature and ram velocity from the simulated results of the retarding potential analyzer data. Adv Space Res , 2003, 32(11): 2361-2366. DOI:10.1016/S0273-1177(03)90566-7 |
| [9] | Klenzing J H, Earle G D, Heelis R A. Errors in ram velocity and temperature measurements inferred from satellite-borne retarding potential analyzers. Physics of Plasmas , 2008, 15: 062905. DOI:10.1063/1.2936270 |
| [10] | Klenzing J H, Earle G D, Heelis R A, et al. A statistical analysis of systematic errors in temperature and ram velocity estimates from satellite-borne retarding potential analyzers. Physics of Plasmas , 2009, 16: 052901. DOI:10.1063/1.3125311 |
| [11] | Bourdeau R E, Whipple E C Jr, Donley J L, et al. Experimental evidence of the presence of helium ions based on explorer VⅢ satellite data. J Geophys Res , 1962, 67(2): 467-475. DOI:10.1029/JZ067i002p00467 |
| [12] | S'eran E. Reconstruction of the ion plasma parameters from the current measurements:mathematical tool. Annales Geophysicae , 2003, 21: 1159-1166. DOI:10.5194/angeo-21-1159-2003 |
 2010, Vol. 53
2010, Vol. 53

