地球物理学报  2010, Vol. 53 Issue (10): 2507-2515   PDF    
引用本文
魏宝君, 田坤, 张旭 等. 定向电磁波传播随钻测量基本理论及其在地层界面预测中的应用. 地球物理学报, 2010, 53(10): 2507-2515, doi: 10.3969/j.issn.0001-5733.2010.10.024.  
Wei B J, Tian K, Zhang X, et al. Physics of directional electromagnetic propagation measurements-while-drilling and its application for forecasting formation boundaries. Chinese J. Geophys. (in Chinese), 2010, 53(10): 2507-2515, doi: 10.3969/j.issn.0001-5733.2010.10.024.  
定向电磁波传播随钻测量基本理论及其在地层界面预测中的应用
魏宝君 , 田坤 , 张旭 , 刘坤     
中国石油大学物理科学与技术学院, 东营 257061
收稿日期 2010-03-15, 2010-09-14 收修定稿
基金项目: 教育部新世纪优秀人才支持计划(NCET-10-0767), 教育部科学技术研究重点项目(109101), 山东省自然科学基金项目(Y2007E06)资助
作者简介: 魏宝君, 男, 1969年生, 博士, 教授, 教育部"新世纪优秀人才支持计划"入选者.1991年毕业于北京师范大学物理系, 1997年、2003年分别获中国石油大学工学硕士、博士学位, 2004~2005年在美国杜克大学从事博士后研究.主要从事应用地球物理和电磁场理论方法研究工作.E-mail:weibj@upc.edu.cn
摘要: 采用水平层状各向异性介质中的磁流源并矢Green函数计算定向电磁波传播随钻测量的幅度衰减和相位移.分析了定向电磁测量的探测范围和对地层界面的灵敏性, 研究了地层各向异性、地层相对倾角和接收天线倾角对定向测量的影响.计算结果表明, 频率越低、线圈距越大、目的层和围岩层电阻率对比度越大, 定向电磁测量的探测范围越大.随着接收天线倾角的增加, 定向幅度衰减在接近地层界面时的变化更加明显, 对地层界面的灵敏性增加.采用对称天线结构可消除定向测量信号在远离地层界面处对地层各向异性和地层相对倾角的依赖, 实现对地层界面的准确预测.
关键词: 定向电磁波传播      随钻测量      地层界面      并矢Green函数      倾斜接收天线     
Physics of directional electromagnetic propagation measurements-while-drilling and its application for forecasting formation boundaries
WEI Bao-Jun, TIAN Kun, ZHANG Xu, LIU Kun     
College of Physical Science and Technology, China University of Petroleum, Dongying 257061, China
Abstract: The amplitude-attenuation and phase-shift of directional electromagnetic propagation measurements-while-drilling are computed via the magnetic-current-source dyadic Green's functions for horizontally stratified anisotropic media. The detection range and the sensitivity to formation boundaries of directional electromagnetic measurements are analyzed. The influence of anisotropy, formation dip angle, and receiver antenna's tilting angle on directional measurements is studied. The results have shown that the directional detection range will increase with decreasing frequency, increasing coil spacing and increasing resistivity contrast between target bed and shoulder bed. The change of directional amplitude-attenuation will become more obvious with increasing receiver antenna's tilting angle when the tool is approaching formation boundary, and thus the sensitivity to formation boundaries will increase. The introduction of symmetrized antenna configuration can remove the dependence of directional signal on anisotropy and formation dip angle when far away from formation boundaries, and thus the formation boundaries can be accurately forecasted..
Key words: Directional electromagnetic propagation      Measurements-while-drilling (MWD)      Formation boundaries      Dyadic Green's functions      Tilted receiver antennas     
1 引言

在石油钻井领域尤其是海上钻井中，电磁波传播随钻测量技术因其在地质导向、实时地层对比评价中具有重要价值而得到广泛开发和应用.自20世纪80年代随着大斜度井和水平井钻井活动的活跃，首次引入电磁波传播随钻测量技术以来，这种技术的探测性能一直在稳步发展.传统的电磁波传播随钻测量技术均遵循着采用共轴发射天线和接收天线的思路，在技术的改进上亦通过采用多种频率和线圈距达到在复杂地质条件下进行多种探测深度测量的目的[1~6].随着定向钻井技术的发展和旋转导向系统的应用，更为复杂的和更难以到达的油气储集层已被钻到并需要进行地层评价，但传统的随钻测量技术因缺乏定向性和方位灵敏特性而不足以对上述复杂的各向异性地层进行评价，也不能对未钻地层界面的位置及方位进行钻前预测从而实现精确地质导向[7, 8].自2000年开始，随着定向电磁波传播随钻测量概念的引入，产生了新一代定向随钻电磁波测井仪器.最具代表性的仪器是Schlumberger公司在2005年推出的深探测定向随钻电磁波电阻率测井仪器PeriScope15[9]和Halliburton公司在2007年推出的方位深探测随钻电磁波电阻率测井仪器ADR[10].这些仪器除含有轴向天线外还含有倾斜天线和横向天线，大大提高了电磁波传播随钻测量技术的定向探测能力、方位灵敏特性和信息量，从而提高了该技术对未钻地层界面位置及方位的钻前预测能力并初步实现了对复杂地层的高精度对比评价.本文采用笔者开发的水平层状各向异性介质中的磁流源并矢Green函数[11~13]对定向电磁波传播随钻测量的基本原理及其在地层界面预测中的应用进行分析.

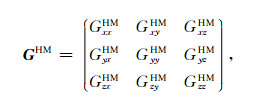
2 基本理论

在地层直角坐标系xyz中，设z轴为地层界面法向，则层状各向异性地层中的磁流源并矢Green函数GHM可表示为如下矩阵形式：

(1)

式中，GxxHM、GyxHM、GzxHM表示x方向单位磁偶极子产生磁场强度的x、y、z分量；GxyHM、GyyHM、GzyHM表示y方向单位磁偶极子产生的磁场强度的x、y、z分量；GxzHM、GyzHM、GzzHM表示z方向单位磁偶极子产生的磁场强度的x、y、z分量.GHM各元素的具体表达式见文献[11]，可采用递推矩阵算法计算[11~13].

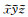
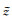
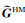
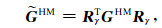
记为仪器直角坐标系，设地层法向在xz平面内相对于仪器轴向的倾角为γ（见图 1，仪器坐标系的y珘轴与地层坐标系的y轴重合），则经坐标转换可将地层坐标系中的GHM转换为仪器坐标系中的.二者之间的转换关系为[14]：

(2)

式中，为坐标系间的转换矩阵.

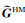
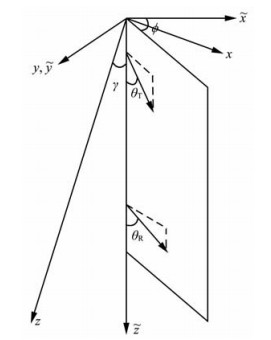
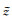
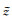
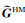
为了计算倾斜线圈系的响应，考虑一个发射-接收天线对之间的信号耦合（图 1）.假设发射天线和接收天线的磁矩均在同一平面内，磁矩方向与仪器轴向之间的夹角分别为θT和θR，磁矩平面的方位角为ϕ.则当仪器绕轴旋转时，发射天线在接收天线处产生的感应电动势将随着方位角ϕ的变化而改变.假设发射线圈的磁矩为MT，由的各分量得到发射天线在接收天线处产生的磁场强度的x分量、y分量和z分量分别为

图 1 仪器坐标系与地层坐标系之间的关系示意图 Fig. 1 Schematic configuration of tool coordinate system and formation coordinate system

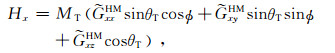
(3a)

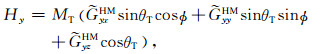
(3b)

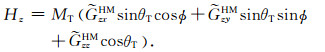
(3c)

接收天线处的总磁场强度为

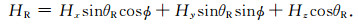
(4)

将式（3）代入式（4），经整理得到：

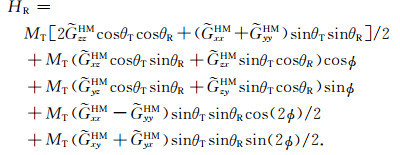
(5)

设发射源随时间的变化关系为exp（iωt），其中ω为角频率，则接收天线的感应电动势可表示为

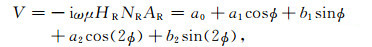
(6)

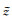
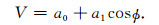
式中NR和AR分别为接收天线的匝数和面积，μ为地层磁导率.系数a0、a1、b1、a2、b2可由式（5）得到.由式（5）和式（6）可以看出，对于传统的电磁波传播随钻测井仪器，由于所有天线的磁矩均沿仪器轴向，即θT=θR=0，式（6）等号右侧只有第1项a0≠0，其余各项系数均为0，测量信号与ϕ无关、不具有方位特性.若发射天线磁矩或接收天线磁矩中只有一个沿仪器轴向，即θT=0或θR=0，则式（6）等号右侧系数a2=0、b2=0.一般情况下发射天线或接收天线只要有一个倾斜，式（6）就与方位角ϕ有关，式中就含有电阻率沿方位角变化的信息以及地层各向异性的信息.一般的定向电磁波传播随钻测井仪器采用发射天线沿仪器轴向、接收天线倾斜的方式[9, 10]，即θT=0.另外，考虑到仪器只在地层xz平面内前进，式（5）中则在式（6）只有a0和a1两个非零系数，式（6）简化为

(7)

即接收天线中的感应电动势随方位角ϕ呈余弦变化.将定向地质导向信号定义为方位角相对的两个方向（ϕ=0°和ϕ=180°）的信号的差别[9, 10]（即最大信号差别），则可定义单个发射-接收天线对之间的定向幅度衰减和定向相位移为

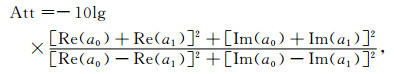
(8a)

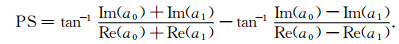
(8b)

对于对称发射-接收天线对[9]，总的定向幅度衰减或定向相位移为两个独立的发射-接收天线对定向幅度衰减或定向相位移之和.

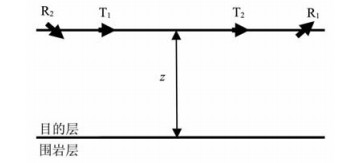
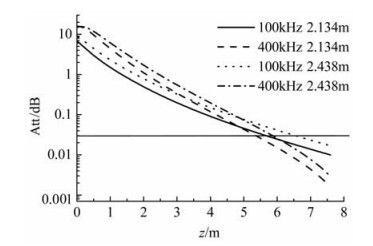
3 定向电磁测量分析 3.1 定向电磁测量探测范围分析

利用式（8）计算Schlumberger公司PeriScope 15仪器线圈距分别为2.134 m和2.438 m的对称定向发射-接收天线对，采用100 kHz和400 kHz频率时在目的层电阻率为50 Ωm、围岩层电阻率为1 Ωm各向同性地层中的定向幅度衰减（接收天线倾角θR=45°）.计算时将仪器置于目的层中、仪器轴线平行于地层界面（即地层相对倾角γ=90°），连续增加仪器到地层界面的距离z（图 2，图中T1/R1与T2/R2互为对称定向发射-接收天线对），可得到如图 3所示的定向幅度衰减随仪器到地层界面距离z的变化关系曲线.由图 3可以看出，随着仪器到地层界面距离的增加，各天线对的定向幅度衰减逐渐减小.当仪器到地层界面距离趋于无穷大时，定向幅度衰减信号趋于0.对于同一线圈距，当仪器到地层界面的距离较小时，采用较高频率时的定向幅度衰减信号较强，但随着仪器到地层界面距离的增加，高频定向幅度衰减信号衰减速度较快，而低频100 kHz的定向幅度衰减信号随仪器到地层界面距离的变化更加平缓.对于同一频率，当仪器到地层界面的距离相同时，线圈距越大，定向幅度衰减的数值越大.根据仪器所允许的灵敏度由图 3可以确定出各天线对的定向探测范围.例如，若仪器所允许的灵敏度为0.03 dB（图 3水平实线），则2.438 m天线对采用100 kHz时的定向探测范围为6.553 m、采用400 kHz时的定向探测范围为5.842 m；2.134 m天线对采用100 kHz时的定向探测范围为5.664 m、采用400 kHz时的定向探测范围为5.334 m.由图 3也可以看出，同一线圈距，若采用较低的频率（如100 kHz）可以增加定向探测范围，但由于变化平缓对距离的分辨率降低；若采用较高的频率（如400 kHz）虽使定向探测范围减小一些但由于随距离的变化明显因而对距离的分辨率升高.由于这种定向电磁信号的探测范围大，当仪器在高阻含油目的层中以较大倾斜角度钻进时可以及早地指示出低阻围岩层或水层的存在，从而可及时调整钻进方向使仪器轨迹始终处在最佳油层部位.

图 2 分析定向电磁测量探测深度时的示意图 Fig. 2 2 Schematic configuration for analyzing the detection range of directional electromagnetic measurements
图 3 各天线对在50/1 Ωm地层中的定向幅度衰减 Fig. 3 Directional amplitude-attenuation of antenna pairs in 50/1 Ωm formation

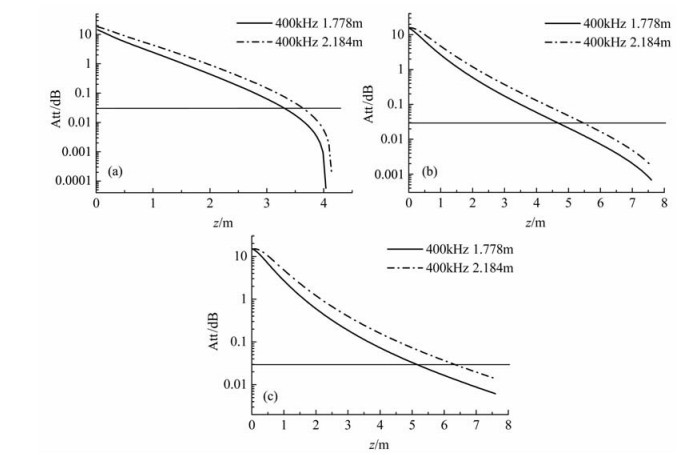
利用式（8）分析线圈距分别为1.778 m和2.184 m的对称定向发射-接收天线对采用400 kHz频率时在不同目的层和围岩层电阻率对比度各向同性地层中的定向幅度衰减，计算结果见图 4.由图 4可以看出，随着目的层和围岩层电阻率对比度的增加，仪器相同灵敏度条件下对应的各天线对的定向探测范围增大.例如，若仪器所允许的灵敏度为0.03 dB（图中水平线），则1.778 m天线对在10/1 Ωm、50/1 Ωm、200/1 Ωm电阻率对比度地层中的定向探测范围分别为3.302 m、4.648 m、5.131 m，2.184 m天线对在10/1 Ωm、50/1 Ωm、200/1 Ωm电阻率对比度地层中的定向探测范围分别为3.632 m、5.436 m、6.299 m.另由图 4可以看出，随着目的层和围岩层电阻率对比度的增加，各天线对定向幅度衰减随仪器到地层界面距离增加而产生的变化更加平缓.

图 4 各天线对在不同电阻率对比度地层中的定向幅度衰减 （a）10/1 Ωm；（b）50/1 Ωm；（c）200/1 Ωm. Fig. 4 Directional amplitud-attenuation of antenna pairs in formation with different resistivity contrast
3.2 定向电磁测量对地层边界的灵敏性分析

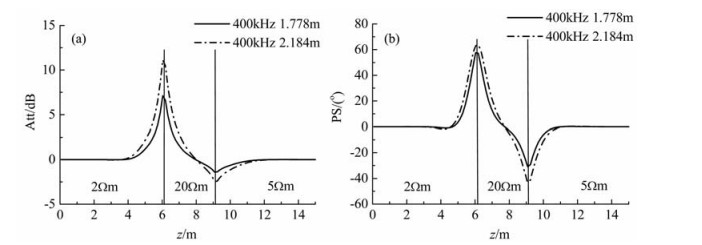
为了分析定向电磁测量对地层边界的灵敏性，利用式（8）计算线圈距分别为1.778 m和2.184 m的对称定向发射-接收天线对采用400 kHz频率时水平穿过三层各向同性地层模型时的定向幅度衰减和定向相位移.模型上下围岩的地层电阻率分别为2 Ωm和5 Ωm，电阻率为20 Ωm的中间高阻目的层的厚度分别为3.048 m和6.096 m，计算结果分别见图 5和图 6.由图 5和图 6可以得到如下结论：（1）若仪器远离具有任意电阻率的地层边界面，则定向幅度衰减和定向相位移的测量信号均为零.（2）当仪器在高阻目的层中接近上部低阻围岩时定向幅度衰减和定向相位移的测量信号均为正，当仪器在高阻目的层中接近下部低阻围岩时定向幅度衰减和定向相位移的测量信号均为负，即在两种情况下反号.（3）当仪器从地层边界面任意一侧接近同一边界面时，测量信号均按相同符号变化方向单调增加或降低.（4）地层边界面两侧电阻率差别越大，测量信号在地层边界上的峰值越大，定向测量信号越强.（5）相同频率下长线圈距发射-接收天线对地层边界的灵敏性要优于短线圈距对称发射-接收天线，尤其是定向幅度衰减信号，且信号在地层边界处的峰值与目的层厚度无关.（6）目的层厚度越小，当仪器稍有偏离时定向测量信号的变化越迅速，目的层厚度越大，当仪器稍有偏离时定向测量信号的变化越缓慢.利用上述符号的改变可以及早预测未钻低阻地层的存在及上下部位，从而及时调整随钻仪器使之一直处于高阻目的层中.

图 5 仪器水平穿过3.048 m厚目的层时的定向响应 （a）定向幅度衰减；（b）定向相位移. Fig. 5 Directional response of the tool passing horizontally through target formation with thickness of 3. 048 m. (a) Directional amplitude-attenuation; (b) Directional phase-shitt.
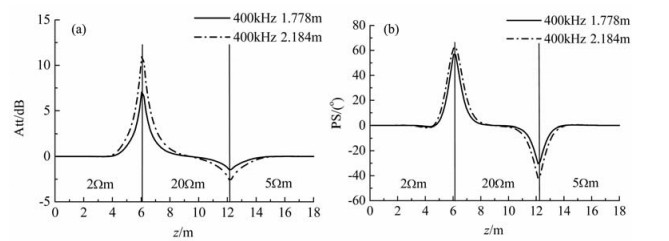
图 6 仪器水平穿过6.096 m厚目的层时的定向响应 （a）定向幅度衰减；（b）定向相位移. Fig. 6 Directional response of the tool passing horizontally through target formation with thickness of 6. 096 m (a) Directional amplitude-attenuation; (b) Directional phase-shitt.
3.3 地层各向异性和相对倾角对定向电磁测量信号的影响分析

为了分析地层相对倾角对定向电磁测量信号的影响，利用式（8）计算线圈距为2.184 m的单个发射-接收天线对和对称发射-接收天线对采用400 kHz频率时以不同倾角γ穿过三层各向同性地层模型时的定向幅度衰减.模型上下围岩的电阻率分别为2 Ωm和1 Ωm，中间目的层的电阻率为20 Ωm、厚度为6.096 m，计算结果见图 7.由图 7可以看出，当地层为各向同性时，单个发射-接收天线对的定向幅度衰减曲线在地层边界面附近受地层相对倾角的影响较大，而对称发射-接收天线对在地层边界面附近受地层相对倾角的影响较小.无论采用对称天线对与否，仪器在远离边界面的地层中定向幅度衰减信号仍为零，与地层相对倾角无关.

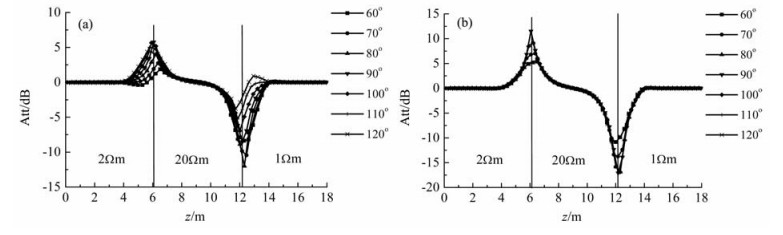
图 7 2.184 m天线对穿过6.096 m厚各向同性目的层时的定向幅度衰减 （a）单个天线对；（b）对称天线对. Fig. 7 Directional amplitude-attenuation of the 2.184 m antenna pair passing through isotropic target formation with thickness of 6.096 m (a) Single antenna pair; (b) Symmetrical antenna pair.

为了分析地层各向异性对定向电磁测量信号的影响，利用式（8）计算线圈距为2.184 m的单个发射-接收天线对和对称发射-接收天线对采用400 kHz频率时以不同倾角γ穿过三层各向异性地层模型时的定向幅度衰减.模型上下围岩的电阻率分别为2 Ωm和1 Ωm，中间目的层为各向异性地层，其水平电阻率Rh=4 Ωm、垂直电阻率Rv=20 Ωm，厚度为6.096 m，计算结果见图 8.由图 8，在各向异性地层边界面附近地层相对倾角对定向电磁测量信号的影响规律类似于图 7.由图 8a ，在远离边界面的各向异性目的层中，单个发射-接收天线对的幅度衰减随地层倾角的变化明显改变，偏离零点.由于地层电参数的精确值一般是事先未知的，图 8a 的这种结果容易导致出现错误判断.由图 8b ，对称发射-接收天线对的幅度衰减在远离边界面的各向异性目的层中仍保持为零，对地层各向异性不再敏感.可见为了进行精确地质导向，采用对称天线对是必要的.

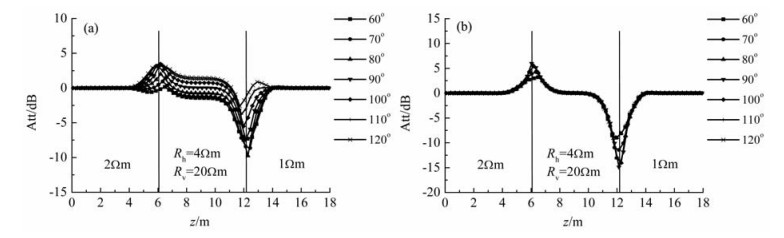
图 8 2.184 m天线对穿过6.096 m厚各向异性目的层时的定向幅度衰减 （a）单个天线对；（b）对称天线对. Fig. 8 Directional amplitude-attenuation of the 2.184 m antenna pair passing through anisotropic target formation with thickness of 6.096 m (a) Single antenna pair; (b) Symmetrical antenna pair.
3.4 接收天线的倾角对定向电磁测量信号的影响分析

在上述讨论中均假设接收天线的倾角θR=45°，下面分析当接收天线的倾角发生改变时定向电磁测量信号的变化规律.图 9为θR=60°时线圈距为2.184 m的对称发射-接收天线对采用400 kHz频率时以不同倾角γ穿过三层各向异性地层模型时的定向幅度衰减.对比图 9和图 8b 可以看出，接收天线倾角的改变只对地层边界面处定向电磁测量信号的峰值产生了影响，并没有导致其它变化，同样可用于精确地质导向.

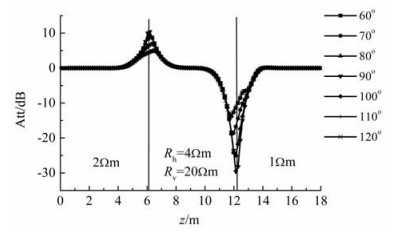
图 9 接收天线倾角为60°时2.184 m对称天线对穿过各向异性目的层时的定向幅度衰减 Fig. 9 Directional amplitude-attenuation of the 2.184 m symmetrical antenna pair passing through anisotropic target formation when the receiver antenna's tilting angle is 60°

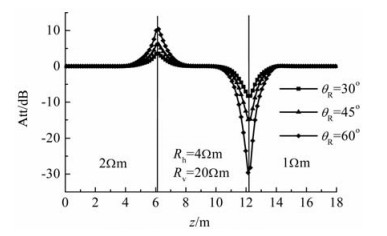
图 10为接收天线的倾角分别为30°、45°和60°时2.184 m对称发射-接收天线对采用400 kHz频率时水平穿过三层各向异性地层模型时的定向幅度衰减.由图 10可以看出，随着接收天线倾角的增加，定向幅度衰减在接近地层边界面时的变化更加明显，在界面处的峰值越大.但需指出的是，随着接收天线倾角的增加，接收天线处接收到的感应电动势的强度越来越弱，从而导致定向电磁测量信号的误差增大，所以接收天线的倾角并不是越大越好.选择θR=45°是一个折衷方案，既保证了定向电磁测量信号对地层边界的灵敏性又考虑到了接收信号的强度.所以PeriScope15和ADR均将接收天线的倾角选择为45°.

图 10 接收天线具有不同倾角时2.184 m对称天线对水平穿过各向异性目的层时的定向幅度衰减 Fig. 10 Directional amplitude-attenuation of the 2.184 m symmetrical antenna pair passing horizontally through anisotropic target formation when the receiver antenna's tilting angles are different
3.5 定向电磁测量信号的方位分辨特性分析

由式（7）知，当仪器发射天线磁矩沿仪器轴向、接收天线倾斜时，接收线圈的感应电动势将随方位角ϕ呈余弦式周期性变化.定义单个发射-接收天线对之间与ϕ相关的定向幅度衰减和定向相位移如下：

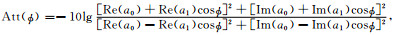
(9a)

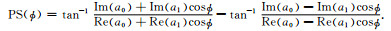
(9b)

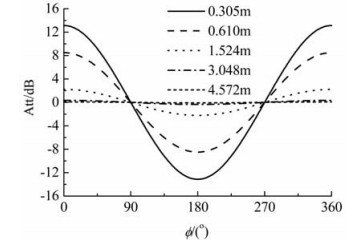
利用式（9）计算2.184 m对称发射-接收天线对采用400 kHz频率时在目的层电阻率为50 Ωm、上围岩层电阻率为1 Ωm地层中的定向幅度衰减.计算时将仪器置于目的层中、仪器轴线平行于地层界面，图 11为仪器到地层界面不同距离时定向幅度衰减随方位角ϕ的变化关系曲线.由图 11可以看出，定向幅度衰减随方位角ϕ呈余弦式周期性变化，其振幅与仪器到地层界面的距离有关.仪器到地层界面的距离越远，振幅越小，在均匀介质中振幅为零.当仪器到地层界面的距离达到一定数值时，若振幅小于仪器所允许的灵敏度，则定向幅度衰减随仪器方位角ϕ的变化可近似看作一条直线，仪器无法探测到低阻围岩层的存在.由图 11知，定向幅度衰减的零点出现在方位角为90°和270°处.若零点不是出现在这两个方位角处，则说明地层界面在方位上出现倾斜并可据此估算方位倾斜角度.另由图 11发现，在仪器旋转过程中当地层界面处于仪器正上方（ϕ=0°）或正下方（ϕ=180°）时定向幅度衰减信号最强.

图 11 2.184 m对称天线对在50/1 Ωm地层中的定向幅度衰减与方位角的关系 Fig. 11 Relation between directional amplitude-attenuation of 2.184 m symmetrical antenna pair and azimuth angle in 50/1 Ωm formation

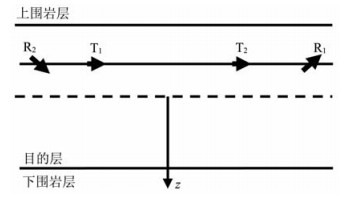
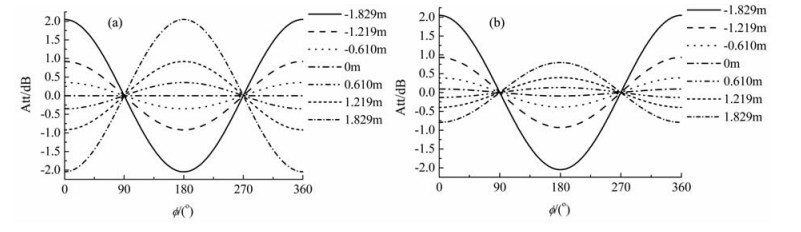
利用式（9）计算2.184 m对称发射-接收天线对采用400 kHz频率时在三层各向同性地层中的定向幅度衰减（图 12）.中间目的层的电阻率为20 Ωm、厚度为6.096 m.以目的层中心为垂向坐标原点，则上围岩层界面垂向坐标为-3.048 m、下围岩层界面垂向坐标为3.048 m，模拟时将仪器置于目的层中、仪器轴线平行于地层界面.首先假设上下围岩层的电阻率均为2 Ωm，图 13a 为仪器在不同垂向坐标情况下定向幅度衰减随方位角的变化关系曲线.由图 13a ，当仪器位于目的层上部时定向幅度衰减随方位角呈余弦变化，且仪器越接近上围岩层界面振幅越大.当仪器位于目的层下部时定向幅度衰减随方位角呈反余弦变化，且仪器越接近下围岩层界面振幅越大，当仪器位于目的层中心时振幅为零.再假设上下围岩层电阻率分别为2 Ωm和5 Ωm，图 13b 为仪器定向幅度衰减随方位角的变化关系.由图 13b ，由于上下围岩层电阻率不同，当仪器偏离目的层中心相同垂向距离时曲线不再反对称，且当仪器位于目的层中心时振幅不为零，振幅为零时对应的仪器位置向下方移动，即向高阻围岩层靠近.下围岩层电阻率越接近于目的层电阻率，这种非对称性越明显，振幅为零时的仪器位置就越向下方移动，定向幅度衰减随方位角的变化关系曲线就越类似于图 11.对比图 13和图 11，若目的层附近只有一个地层界面，则当仪器到地层界面距离改变时定向幅度衰减随方位角的变化不会反相；若目的层附近有两个地层界面，则当仪器到地层界面距离改变时定向幅度衰减随方位角的变化出现反相.

图 12 上下围岩均存在时分析定向电磁测量信号方位分辨特性的模型 Fig. 12 Model for analyzing the azimuthal resolution of directional electromagnetic measurement signal when there are shoulder beds both above and below
图 13 上下围岩均存在时2.184 m对称天线对定向幅度衰减随方位角变化关系 （a）上下围岩层电阻率均为2 Ωm；（b）上下围岩层电阻率分别为2 Ωm和5 Ωm. Fig. 13 Relation between directional amplitude-attenuation of 2.184 m symmetrical antenna pair and azimuth angle when there are shoulder beds both above and below. (a) The resistivity of shoulder beds both above and below is 2 Ωm; (b) The resistivities of above shoulder and below shoulder are 2 Ωm and 5 Ωm respectively.
4 结论

本文采用水平层状各向异性介质中的磁流源并矢Green函数对定向电磁波传播随钻测量仪器的响应进行数值模拟，计算结果表明：

（1）频率越低、线圈距越大、目的层和围岩层电阻率对比度越大，则在仪器相同灵敏度条件下定向电磁测量的探测范围越大.（2）采用对称天线结构可消除定向电磁测量信号在远离地层界面处对地层各向异性和地层相对倾角的依赖，实现对地层界面的准确预测.当仪器接近围岩层时，利用定向电磁测量信号符号的改变可以及早预测未钻低阻地层的存在及上下部位，从而及时调整仪器使之一直处于高阻目的层中.（3）随着接收天线倾角的增加，定向幅度衰减在接近地层界面时的变化更加明显，对地层界面的灵敏性增加.但考虑到接收信号的强度，接收天线的倾角并不是越大越好.（4）利用定向电磁测量信号的方位分辨特性可以估算地层界面的方位倾斜角度.

参考文献
[1] Rodney P F, Wisler M M. Electromagnetic wave resistivity MWD Tool. SPE Drilling Engineering, Oct. 1986. 337~346
[2] Bittar M S, Rodney P F, Mack S G, et al. A multiple-depth-of-investigation electromagnetic wave resistivity sensor:theory, experiment, and field test results. SPE Formation Evaluation, Sep. 1993. 171~176
[3] Meyer W H. New two frequency propagation resistivity tools. SPWLA 36th Annual Logging Symposium, Paper XX, June 1995
[4] Bittar M S, Rodney P E. The effects of rock anisotropy on MWD electromagnetic wave resistivity sensors. The Log Analyst , 1996, 37(1): 20-30.
[5] Bittar M S. Fixed depth of investigating log for LWD resistivity tool. SPE Annual Technical Conference and Exhibition, Transactions, SPE Paper 84098, October 2003
[6] Iverson M. Geo-steering using ultra-deep resistivity on the Grane field Norwegian North Sea. SPWLA 44th Annual Logging Symposium, Paper J, June 2003
[7] Bittar M S. Electromagnetic wave resistivity tool having a tilted antenna for determining the horizontal and vertical resistivities and relative dip angle in anisotropic earth formations. US Patent:6163155, 2000-12-19
[8] Bittar M S. Electromagnetic wave resistivity tool having a tilted antenna for geosteering within a desired payzone. US Patent:6476609, 2002-11-05
[9] Li Q, Omeragic D, Chou L, et al. New directional electromagnetic tool for proactive geosteering and accurate formation evaluation while drilling. SPWLA 46th Annual Logging Symposium, Paper UU, June 2005
[10] Bittar M S, Klein J, Beste R, et al. A new azimuthal deep-reading resistivity tool for geosteering and advanced formation evaluation. SPE Annual Technical Conference and Exhibition, Transactions, SPE Paper 109971, November 2007
[11] 魏宝君, 王甜甜, 王颖. 用磁流源并矢Green函数的递推矩阵方法计算层状各向异性地层中多分量感应测井响应. 地球物理学报 , 2009, 52(11): 2920–2928. Wei B J, Wang T T, Wang Y. Computing the response of multi-component induction logging in layered anisotropic formation by the recursive matrix method for magnetic-current-source dyadic Green's function. Chinese J. Geophys. (in Chinese) , 2009, 52(11): 2920-2928.
[12] Wei B J, Zhang G J, Liu Q. Recursive algorithm and accurate computation of dyadic Green's functions for stratified uniaxial anisotropic media. Science in China (Series F) , 2008, 51(1): 63-80. DOI:10.1007/s11432-007-0069-7
[13] 杨锦舟, 魏宝君, 林楠. 倾斜线圈随钻电磁波电阻率测量仪器基本原理及其在地质导向中的应用. 中国石油大学学报(自然科学版) , 2009, 33(1): 44–49. Yang J Z, Wei B J, Lin N. Basic theory of electromagnetic wave resistivity measurement while drilling tool with tilted antennas and its application for geo-steering. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese) , 2009, 33(1): 44-49.
[14] 汪宏年, 陶宏根, 姚敬金, 等. 用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应. 地球物理学报 , 2008, 51(5): 1591–1599. Wang H N, Tao H G, Yao J J, et al. Study on the response of a multicomponent induction logging tool in deviated and layered anisotropic formations by using numerical mode matching method. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1591-1599.