在频率域电磁法勘探中,随着发射源功率的增大,收发距可能达数千公里,较传统意义上的收发距大很多,这时必须考虑地球半径及电离层的影响,基于水平大地模型得到的水平电偶极子源激发的电磁场表达式不再适用.目前国内已经开始了这方面的应用研究,赵国泽研究了使用人工源超低频率电磁波监测地震[1];底青云等研究了水平地球模型下的长偶极子大功率源激发的场[2~5],并将其用于资源勘探[6].
在通讯领域,频率范围在n×10-2~n×103之间属于极低频率范围.研究这个频段的电磁波在空气的传播时,一般认为以电离层、地球作为边界的空气层形成一个球层波导腔,而以往大多研究者都只研究空气层中的电磁波传播,鉴于地球介质和电离层都是良导体,往往在地球-空气界面和电离层-空气界面处用阻抗边界条件构成闭合的方程求解未知系数[7~11],阻抗边界条件是基于水平极化的电磁波入射到水平无限大导电介质界面上得到的近似边界条件.对地球物理应用来说,所研究的对象是地球介质,而且场测量往往在地表或地下,在空气-地球界面上使用阻抗边界条件,则无法满足实际的需要,故在场的求解过程中,需在地球-空气界面上使用电磁场的一般过渡边界条件,求得地表或地下的电磁场的表达式,通过分析这些公式才能得到地球介质中电磁场的传播特性.
本文研究电离层-空气-均匀地球模型中置于地表的水平电偶极子源在地球介质中激发的电磁场.从一般电磁场原理出发,使用Debye势的方法,结合电磁场的一般过渡边界条件,导出了在电离层-空气-地球模型中置于地表的水平电偶极子在均匀地球模型中激发的地下电磁场的级数表达式;由于解是一个无限的球Bessel函数级数表达式,而大变量球Bessel函数的计算非常困难,考虑到地球半径很大,对球Bessel函数使用指数函数近似,简化球Bessel函数的计算过程;由于级数收敛非常缓慢,为了加快收敛,使用加速算法[9].
为验证解和计算过程的正确性,在理论上取地球半径趋于无穷大,电离层高度无限大,得到了均匀半空间的解;在数值计算上,一方面,计算无电离层时的近场区的电磁场并将其与均匀半空间的解作了比较,结果非常一致;另一方面,计算了频段1~50 Hz内的电磁场,得到了前6个Schamann共振频率,完全和理论结果吻合;此外还结合野外观测数据,将计算结果和实际数据进行比较,在可确定的误差范围内两者是一致的.以上表明,所得结果是可靠的.
2 场表达式设时间因子为exp-iωt,在球坐标系中,由于点源是局限在有限的空间中,故在大部分的空间中都不存在源,而无源的Maxwell方程的分量表达式为[12]:
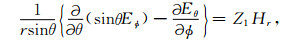
|
(1) |
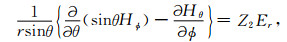
|
(2) |
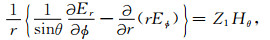
|
(3) |
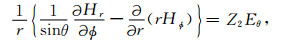
|
(4) |
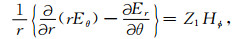
|
(5) |

|
(6) |
式中
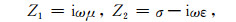
|
(7) |
其中r、θ、ϕ是球坐标系中径向变量、仰角、方位角;ω为圆频率,μ磁导率,ε为介电常数,σ介质电导率.边界条件为电磁场切向分量Eϕ、Eθ、Hϕ、Hθ在电离层-空气界面、空气-地球界面上满足连续性条件.注意,此处使用的是一般的过渡边界条件,而非阻抗边界条件.
上面方程中,电场和磁场相互耦合,无法直接求解,将电磁场沿着地球径向方向分解为两种情形:(一)电场存在径向分量,磁场无径分量,即所谓的横磁场,记为TM;(二)电场无径向分量,磁场存在径向分量,所谓的横电场,记为TE.引入电磁场的Debye势Φ、Ψ[7, 12],由(1)~(7)式及电磁场切向分量连续的边界条件导出Φ、Ψ所满足的方程及边界条件如下:
(1)TE情形

|
(8) |
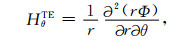
|
(9) |

|
(10) |
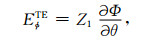
|
(11) |
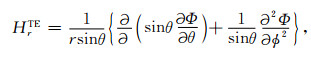
|
(12) |
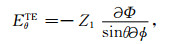
|
(13) |
Φ在边界上应满足如下的边界条件:
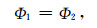
|
(14) |
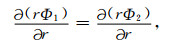
|
(15) |
(2)TM情形
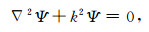
|
(16) |
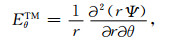
|
(17) |
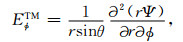
|
(18) |

|
(19) |
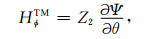
|
(20) |
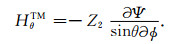
|
(21) |
Ψ在边界上应满足如下的边界条件:
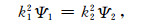
|
(22) |
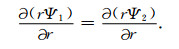
|
(23) |
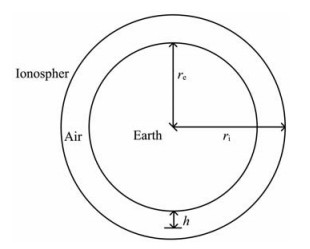
模型结构如图 1所示,在空气腔中,将总场分解为电偶极子源激发的一次场Erp、Hrp和由一次场激发的二次场Ers、Hrs之和,即Er=Erp+Ers、Hr=Hrp+Hrs.将一次电场和磁场在球坐标系中的径向分量求出,然后再使用球Bessel函数和Legendre函数展开,具体过程复杂冗长,请参阅文献[7],然后根据一次场的形式,导出各层中Debye的形式解,然后根据边界条件导出各层Debye势中的未知系数,即可得到各层中的电磁场的解.由此导出电离层-空气-均匀地球模型中置于地表的水平电偶极子激发的地球介质中的电磁场的表达如下:
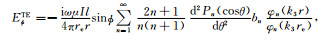
|
(24) |
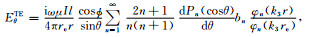
|
(25) |
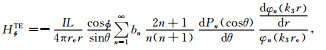
|
(26) |
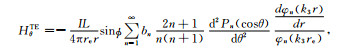
|
(27) |
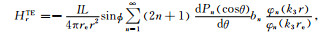
|
(28) |
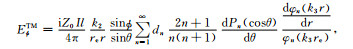
|
(29) |
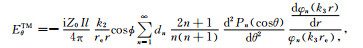
|
(30) |
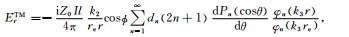
|
(31) |
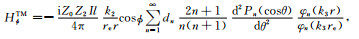
|
(32) |

|
(33) |
|
图 1 地球-电离层截面图 Fig. 1 section view of the earth-ionosphere |
其中kj2=ω2εμ+iωμσj,j=1,2,3.j=1为电离层,j=2为空气,j=3表示地球介质;re为地球半径,ri表示地心到电离层的距离,h=ri-re,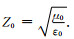
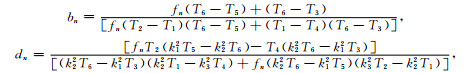
|
其中

|
而
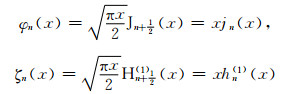
|
为球Bessel函数的记法表示.
上面的公式是置于地表水平电偶极子在均匀地球模型中的地下电磁场一般表达式,是本文首次在电磁场一般性边界条件下导出的,在近场区、过渡区、波区均精确成立.它不同于使用阻抗边界条件得到的电磁场表达式,其仅在波区成立,因为阻抗边界条件是基于水平极化的电磁波入射到水平无限大导电介质界面上得到的近似边界条件[7];而且,阻抗边界条件使电磁场计算局限于地面-电离层之间形成的球形波导腔中,恰恰忽略了我们感兴趣的地下电磁场的分布.
3 电磁场的计算
在地球物理中,测点往往在垂直平分水平电偶极子的水平直线附近,这条直线的方位角ϕ=π/2,故在计算中,取ϕ=π/2,故只需要计算EϕTE、HθTE、HrTE、EϕTM、HθTM.上面公式中,大阶数的球Bessel函数的变量是kr,其中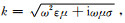
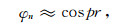
|
(34) |
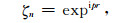
|
(35) |
其中: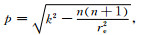
则:
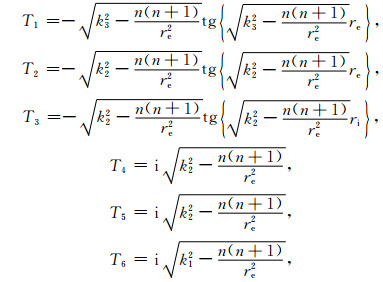
|
而
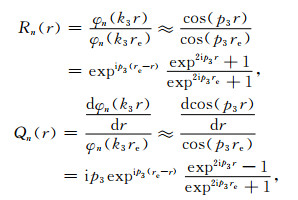
|
当n→∞时,
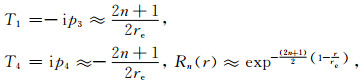
|
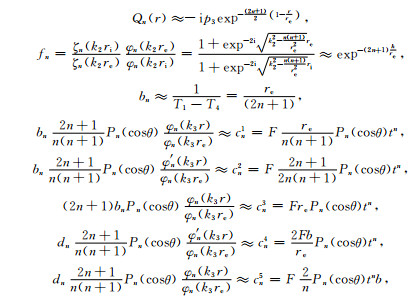
|
其中
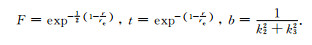
|
下面的恒等式成立[9]:
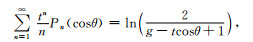
|
(36) |
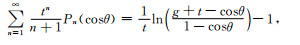
|
(37) |
其中
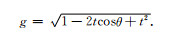
|
则得到

|
(38) |
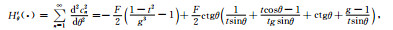
|
(39) |
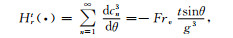
|
(40) |
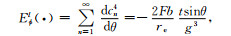
|
(41) |
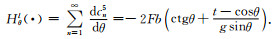
|
(42) |
采用加速算法[9],电磁场表示成如下的形式:

|
(43) |
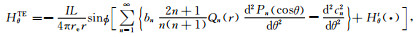
|
(44) |
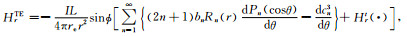
|
(45) |
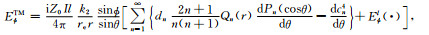
|
(46) |
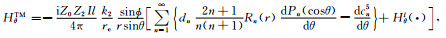
|
(47) |
下面确定电磁场表达式(24~33)和均匀半空间解的表达式的关系.地球半径re趋于无穷大时,可以将地球看成水平均匀大地,在收发距x=reθ固定时,当re→∞,θ→0,在θ很小时,使用如下的近似公式[8]:
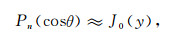
|
(48) |
其中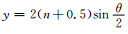
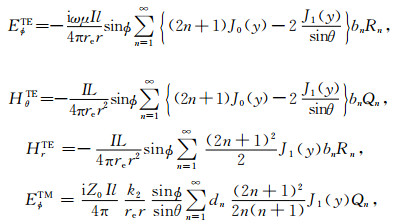
|

|
当h→∞且re→∞时,取k22=0,记:x=reθ,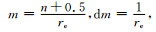
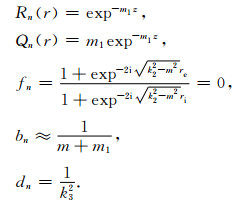
|
其中
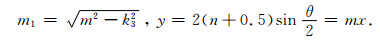
|
将求和变换为积分,得到如下的总场表达式:
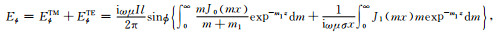
|
(49) |
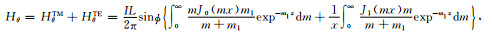
|
(50) |
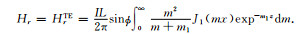
|
(51) |
上面的解和无电离层的水平均匀大地模型的解是一致的[13].这是结果正确性的一个理论证明.
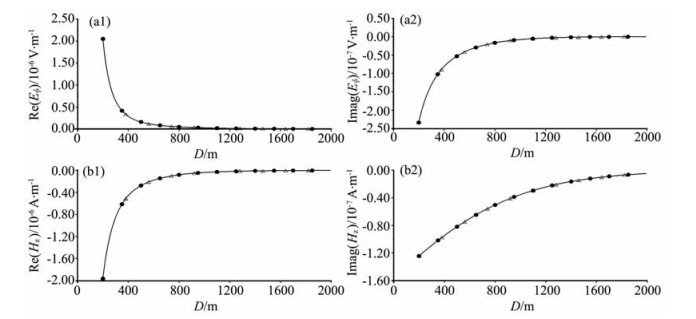
4 解的正确性的计算验证及算例理论上,使用公式(43)~(47)计算小收发距的Eϕ、Hr,其与均匀水平大地半空间的场进行比较[13],两者应该是一致的.在均匀半空间的场表达式中,坐标系中的Eϕ、Hr对应于直角坐标系中Ex、Hz,而Ex、Hz这两个场量存在解析表示式,无需涉及解中的Bessel函数的近似计算.我们取地球半径为6371 km,地球电导率为σe=0.01 S·m-1,源的频率为100 Hz,源的电偶极矩Il=1,测线所在方位角ϕ=π/2,计算2 km以内不存在电离层时地表的Eϕ、Hr,计算结果与均匀水平大地半空间的场进行比较见图 2,其中x轴为收发距D=reθ.可见,两者确实符合很好,这是理论计算正确性的又一个证明.
|
图 2 均匀地球模型的解和均匀半空间解的比较 方位角ϕ=π/2,f=100 Hz.黑点表示均匀地球模型的解,中空三角表示均匀半空间的解 Fig. 2 Comparison between solutions for homogeneous earth model with the analytical solution for homogeneous half space Azimuth is ϕ=n/2 and frequency is f=100 Hz. Black dot denote the solution for homogeneous earth model; hollow triangle denote the solution for homogeneous half space. |
再者,以电离层和地球介质为边界的空气层构成了一个波导腔,当电磁波在其中传播时,在某些频率上,会产生所谓的谐振效应,这时波导腔中存在所谓的驻波,这就是Schumann谐振.谐振频率与地球半径和空气中的波长有关的,表达式如下[14]:
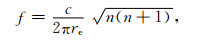
|
(52) |
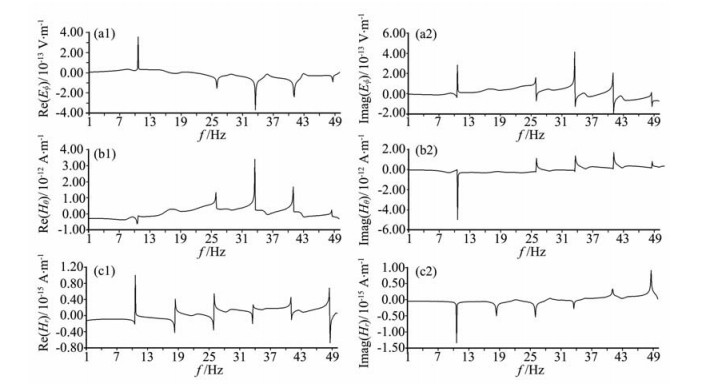
其中c为真空中的光速,n为共振模的编号.前六个共振频率为:f1=10.6 Hz,f2=18.3 Hz,f3=26.0 Hz,f4=33.5 Hz,f5=41.1 Hz,f6=48.6 Hz.通过本文的计算结果也可以确定这些谐振频率.取地球半径6371 km,电离层高度为70 km,地球电导率为σe=0.01 S·m-1,电离层电导率为σi=10-5 S·m-1,频率的采样间隔为0.1 Hz,电偶极矩Il=1,计算点的方位角ϕ=π/2,收发距D=5000 km,计算结果见图 3,存在六个共振峰,其中第二共振峰在Eϕ、Hθ图上不明显,在Hr图上明显突出.因为f=18.3 Hz电磁波在空气中的波长为1.64×104 km,其中四分之一波长为4.1×103 km;而从激发源发出电磁波的第一个波节就在四分之一处,而收发距D=5000 km的点正好在波节附近,故对应此频点的电磁场值较小.计算的谐振频率与理论Schumann谐振频率相同,证明在远区的结果同样可靠.
|
图 3 固定点ϕ=π/2,D=5000 km上不同频率的电偶极子源激发的电磁场 Fig. 3 Electromagnetic fields at point ϕ=π/2, D=5000 km excited by electrical dipole source for differential frequency |
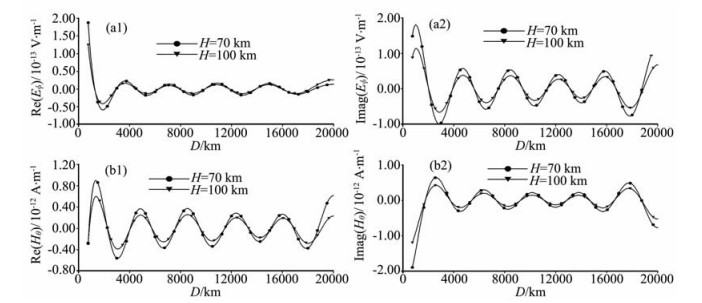
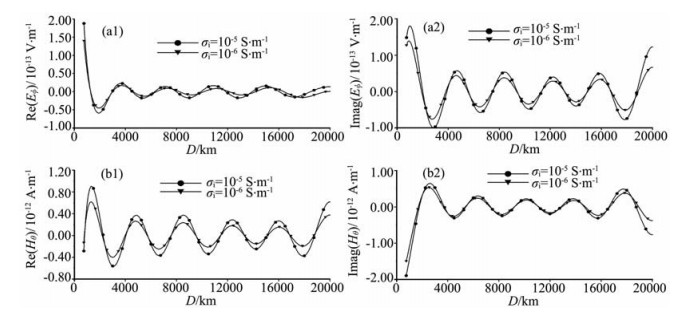
最后,文献[1]报道了在首都圈内的地震台上测量俄罗斯的位于科拉半岛Murmansk附近(Zevs台)超低频发射台的80 Hz的电磁信号,并给出了近东西向水平电场和近南北向水平磁场的功率谱的测量结果.为了和文献[1]的结果比较,我们研究80 Hz电磁波的传播特性,需要考虑电离层参数的变化对电磁场影响.为了和文献[1]中的结果进行比较,取地球电导率σe=0.04 S·m-1.图 4、图 5是地球电导率为σe=0.04 S·m-1,不同电离层高度、电离层电导率不同时电磁场的比较结果,从图中可以发现,电离层参数的变化引起的电磁场的变化是可观的,并且电离层高度的变化只会引起电磁场幅值的变化,电离层升高,地表的电磁场的幅值相应地减少,计算结果表明,在电离层电导率为σi=10-5 S·m-1时,电离层由70 km升高到100 km时,波峰处场强度减小可以达到40%;当电离层高度h=70 km固定,电离层电导率由σi=10-5 S·m-1降为σi=10-6 S·m-1,波峰处电磁场强度的变化可以达到50%之多,由此可见电离层参数变化对电磁场强度的影响非常大,但是,基于如下公式计算的视电阻率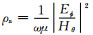
|
图 4 电离层高度取不同值时电磁场的比较图 Fig. 4 Comparison for electromagnetic fields for the different height of ionosphere |
|
图 5 电离层电导率取不同值时电磁场的比较图 Fig. 5 Comparison for electromagnetic fields for the different conductivity of ionosphere |
基于上面四个方面关于理论公式和计算结果正确的证明,我们研究不同频率的电磁波在地表的传播以及同一频率的电磁波在地下不同深度的传播.取地球电导率为0.01 S·m-1,电离层电导率为10-5 S·m-1,电离层高度70 km;测线方位角ϕ=π/2,点距50 km.
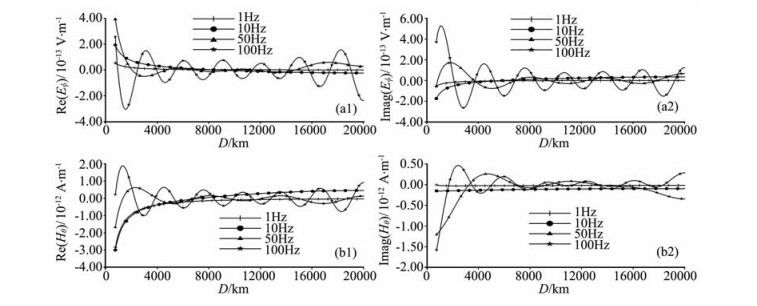
图 6是不同频率的水平电偶极子源激发的电磁场.由图可见,频率越小,场值也越小,而且电磁场在θ方向是以该频率的电磁波真空中的波长传播的,并且幅度非常稳定,衰减很小.其实电磁波在电离层-空气-地球组成的波导中传播是通过电场在电离层中激发出二次感应电流,然后电流激发磁场,随时间变化的磁场又激发出电场,这个过程相互交替,电磁场就在地球表面附近的空气中传播出去.显然,电场强度是和频率相关的,频率越大,电场强度越大,故激发的二次场也就越大,这就是频率大,电磁场幅值大的原因;在θ=π即收发距D=2×104 km,或者说在电偶极子源关于地球的对极点附近,电磁波同相叠加,出现了电磁场幅值的增强现象.由图可见,频率大于10 Hz时,即大于第一个Schumann共振频率时,电磁波在空气的波长小于地球周长,则存在电磁场为零的波节,由于在波节附近,电磁场很小,所以对野外观测来说,应该尽量避免在波节处观测,而选择在波峰处观测可以提高观测数据的质量.
|
图 6 不同频率电偶极源激发的电磁波在地表的传播 Fig. 6 The electromagnetic fields excited by different frequencies electric dipole source propagating on Earth's surface |
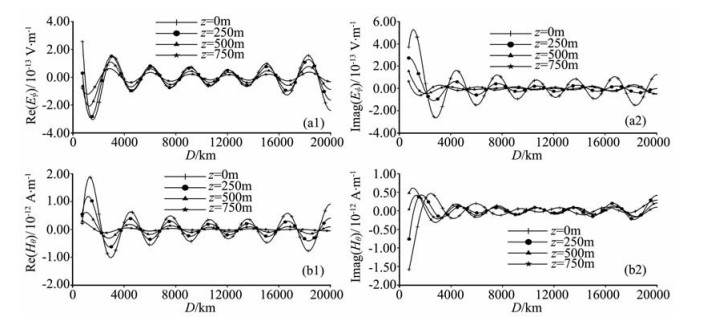
图 7是频率100 Hz的水平电偶极子源激发的电磁波在地下不同深度的传播图.在水平方向上,电磁场具有的波长为3×103km,在电偶极子源关于地球的对极点附近,由于波的同相叠加,电磁场增大.在z方向,总体上电磁场是衰减的,但是,在对极点附近磁场的虚部Imag(Hθ)在z=250 m的值比其在z=0的值大,出现了反常.解释如下,由于地球半径很大,认为在电偶极子源关于地球对极点附近可以使用无限大均匀半空间近似,取θ方向为y方向,ϕ方向为x方向,在对极点建立局部直角坐标系.假设在地表垂直入射x方向线性极化的电场Ex=E0cos(ky),而在地下,▽2Ex+k12Ex=0,故地下的电场为Ex=E0cos(ky)eik1z,其中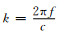
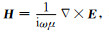
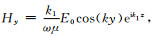
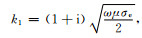
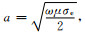
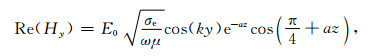
|
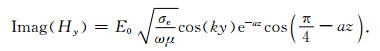
|
|
图 7 频率为100 Hz的电偶极子源激发的电磁波在地下不同深度的传播 Fig. 7 The electromagnetic wave excited by electric dipole source of 100 Hz propagating in the different depth in the earth |
由上面的公式可见,磁场Hy虚部中的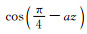

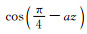
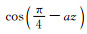
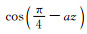
通过简单的地球-电离层模型,计算了超低频人工源电磁波信号在地球表面及地下的传播,发现超低频电磁波信号在地表有如下的传播特性:
(1)在电离层的作用下,电磁波信号在几千公里以外传播幅度衰减很小,幅度非常稳定;
(2)频率越低,电磁波信号也越弱;
(3)电离层参数(高度、电导率)对电磁波的影响很大,电离层升高或电导率降低,可以引起电磁场幅度大约50%的减少,但由电场和磁场得到的视电阻率几乎没有变化,非常稳定.
(4)地下的电磁场在从地表向下的方向上衰减较快.
研究结果对了解超低频率电磁波在地表的传播特性、制定野外观测方案提供重要依据.由于地球-电离层是一个复杂的系统,实际情况的模拟还要考虑到地球表面的海洋和陆地的不均匀性以及地球的分层结构、电离层结构的复杂性等,值得进一步深入研究.
| [1] | 赵国泽, 陆建勋. 利用人工源超低频电磁波监测地震的实验与分析. 中国工程科学 , 2003, 10(5): 27–33. Zhao G Z, Lu J X. Monitoring & analysis of earthquake phenomena by artificial SLF waves. Engineering Science (in Chinese) , 2003, 10(5): 27-33. |
| [2] | 底青云, 王光杰, 王妙月, 等. 长偶极大功率可控源电磁波响应特征研究. 地球物理学报 , 2008, 51(6): 1917–1928. Di Q Y, Wang G J, Wang M Y, et al. Study of the long bipole and large power electromagnetic field. Chinese J.Geophys. (in Chinese) , 2008, 51(6): 1917-1928. |
| [3] | 底青云, 王光杰, 王妙月, 等. 长偶极大功率可控源激励下目标体电性参数的频率响应. 地球物理学报 , 2009, 52(1): 275–280. Di Q Y, Wang G J, Wang M Y, et al. Frequency response characteristics of target electric property with long bipole large power control source. Chinese J.Geophys. (in Chinese) , 2009, 52(1): 275-280. |
| [4] | 李帝铨, 底青云, 王妙月. 电离层-空气层-地球介质耦合下大尺度大功率可控源电磁波响应特征研究. 地球物理学报 , 2010, 53(2): 411–420. Li D Q, Di Q Y, Wang M Y. Study of large scale large power control source electromagnetic with "earth ionosphere" mode. Chinese J. Geophysics. (in Chinese) , 2010, 53(2): 411-420. |
| [5] | 陈小斌, 赵国泽. 关于人工源极低频电磁波发射源的讨论--均匀空间交流点电流源的解. 地球物理学报 , 2009, 52(8): 2158–2164. Chen X B, Zhao G Z. Study on the transmitting mechanism of CSELF waves:response of the a1ternating current point source in the uniform space. Chinese J. Geophys. (in Chinese) , 2009, 52(8): 2158-2164. |
| [6] | 卓贤军, 赵国泽. 一种资源探测人工源电磁新技术. 石油地球物理勘探 , 2004, 39(Suppl.): 114–117. Zhuo X J, Zhao G Z. A new technique of EM controlled source sounding for resource prospecting. Oil Geophys. Prosp. (in Chinese) , 2004, 39(Suppl.): 114-117. |
| [7] | Fock V A. Electromagnetic Diffraction and Propagation Problems. Oxford, London, Edinburgh, New York, Paris, Frankfurt: Pergamon Press, 1965 . |
| [8] | Janis Galejs. Terrestrial Propagation of Long Electromagnetic Waves. Oxford, New York, Toronto, Sydney, Braunschweig: Pergamon Press, 1972 . |
| [9] | Donald E Barrick. Exact ULF/ELF dipole field strengths in the earth-ionosphere cavity over the Schumann resonace region:Idealized boundaries. Radio Science , 1999, 34(1): 209-227. DOI:10.1029/1998RS900014 |
| [10] | Wait J R. Electromagnetic Waves in Stratified Media. Oxford, London, New York, Paris: Pergamon Press, 1962 . |
| [11] | Arthur D Watt. VLF Radio Engineering. Pregamon Press, 1967 . |
| [12] | Max Born, Emil wolf. Principles of Optics. Cambridge University Press, 1999 . |
| [13] | 何继善. 可控源音频大地电磁法. 长沙: 中南工业大学出版社, 1990 . He J S. CSAMT Method (in Chinese). Changsha: Press of Central South University of Technology, 1990 . |
| [14] | Jackson J D. Classical Electromagnetics. (3rd). Johan Willey & Sons, INC, 1998 . |
 2010, Vol. 53
2010, Vol. 53


