2. 中国科学院地质与地球物理研究所, 北京 100029;
3. 中国科学院力学研究所 LHD实验室, 北京 100190
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. LHD Lab Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
经典的达西定理和饱和度方程是孔隙介质中的多相流动最常用的本构关系,该方程采用相对渗透系数函数描述多相流动[1, 2],没有考虑相界面(Phase interface)及其对流场的影响.在高雷诺数条件下,惯性与黏性效应、孔隙介质对流体质点的拖拽作用是不可忽略,且达西定理不成立.文献[3]考虑了惯性和黏性等物理机制,从微观守恒方程控制体积平均思想出发,推导出孔隙介质流动的质量和动量守恒方程,并应用于液滴对孔隙介质的撞击过程[4]、超临界二氧化碳咸水层地质封存的瑞利-泰勒不稳定性[5]以及波在孔隙介质中的传播[6]等多相流动问题的数值计算.
孔隙介质中流场的计算精度取决于动量方程的离散格式.孔隙介质中流动的动量方程离散格式主要是积分有限差分方法[7]、中心差分格式[8]、自适应多尺度有限体积法以及多尺度有限元和流函数混合法[9]等.时空守恒元/解元方法(CE/SE)[10]是一种双曲型偏微分方程的全新高精度计算格式.CE/SE格式构造简单、物理意义明确,提高了计算精度和强间断分辨率.目前已发展到高阶精度的六面体划分方案[11~15],并应用于计算孔隙介质单相流动问题中[16].但是,尚未见到CE/SE方法在孔隙介质中多相流动问题上的应用.
多相流计算需要解决物质界面位置和形状及其随时间演变的数值方法.文献[6]和文献[17]分别采用流体体积法、水平集方法(LevelSet Method)捕捉孔隙介质中的两相流动相界面.近年来Enright等[18]提出的杂交粒子水平集方法(HybridParticle LevelSetMethod)更是大幅度提高了精度,但至今尚未见到其在孔隙介质多相流问题上的应用.
综上所述,关于孔隙介质多相流问题,数值模拟有待更深入的研究.本文以张德良等[11, 15]提出的基于四边形网格守恒元和解元的划分方法为基础,同时结合杂交粒子水平集方法,提出一套用于求解二维Euler型孔隙介质多相流的CE/SE计算方法.通过溃坝和液滴在重力作用下的运动和变形问题的数值模拟,对方法的精度和有效性进行验证.本文目的是将CE/SE方法推广到计算二维孔隙介质多相流问题中.
2 控制方程饱和孔隙介质中,二维非稳态不可压缩黏性流体的广义N-S方程欧拉守恒形式可以写为[16]
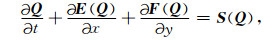
|
(1) |
定义无量纲Reynolds数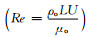
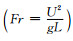
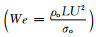
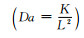
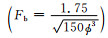
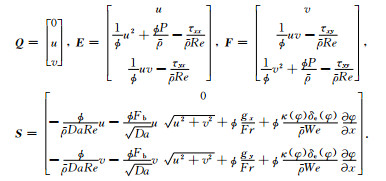
|
(2) |
其中ρ是当地流体的密度,u和v分别是x和y方向的速度,P是流体孔隙压力,ϕ是孔隙度,κ(φ)是界面曲率,
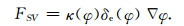
|
(3) |
为了避免界面处的数值振荡,定义Heaviside函数,对界面附近的密度和黏性进行适当光滑[18]:
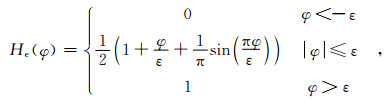
|
(4) |
则密度和黏性系数光滑为
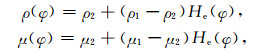
|
(5) |
式中ρ1和ρ2以及μ1和μ2分别是界面两侧的密度和黏性系数.
3 杂交粒子水平集方法孔隙介质多相流计算的主要困难在于如何高精度地捕捉物质界面,需要解决物质界面位置和形状及其随时间演变的数值方法.本文采用Osher和Sethian[20]提出的水平集方法(LevelSetMethod)捕捉相界面.
首先构造水平集函数φ=φ(r,t),使运动界面Γ(t)在任意时刻恰好是函数φ的零等值面[20],即
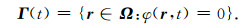
|
(6) |
根据孔隙介质单元控制体积等效平均方法[4],本文将孔隙介质中水平集函数的输送方程扩展为
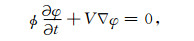
|
(7) |
式中,V=(u,v)是流体的渗流速度.采用五阶WENO格式和Runge-Kutta方法分别离散空间导数和时间导数[21].传统的水平集方法数值格式的耗散效应随着时间的推进容易导致质量或体积丢失,本文采用杂交粒子水平集方法(Hybrid Particle Level Set Method)[18],把基于示踪点粒子的Lagrangian方法和水平集方法结合起来,提高了水平集方法的计算精度.示踪点粒子满足Lgrangian运动方程:
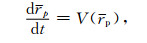
|
(8) |
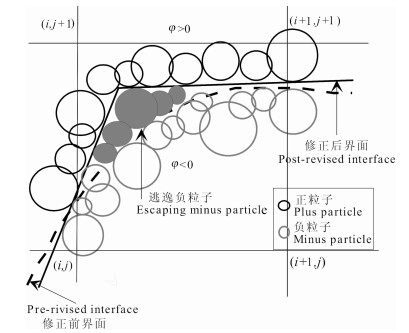
式中,rp是示踪点粒子位置的坐标,V(rp)是其运动速度.采用三阶精度的Runge-Kutta法求解方程(8)的时间推进.由于数值方法的抹平效应,会出现逃逸粒子,使水平集函数表示的界面位置和示踪点粒子表示的界面位置出现偏差,从而需要定义示踪点粒子局部球形水平集函数,对界面位置进行修正[18],修订过程如图 1所示.方程(1)、(5)和(6)构成孔隙介质多相流封闭方程组.
|
图 1 示踪点粒子位置误差修正示意 Fig. 1 Schematic map of the location rectification of tracing particles |
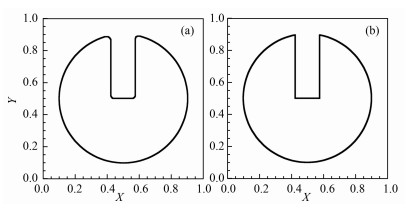
通过Zalesak问题[18]验证粒子水平集方法的计算精度与守恒性.具有缺口的圆周在旋转速度场的作用下发生旋转运动,观察一定时间后圆周的边界变化情况.计算区域大小为1.0×1.0,网格点数为401×401,时间步长为0.0015.旋转2π后,水平集方法计算结果如图 2a,粒子水平集方法如图 2b所示.对比图 2a和图 2b发现两种方法都能准确地给出界面的位置,但水平集方法计算的尖角被抹平,由于粒子水平集方法引入了粒子修正,旋转2π后界面尖角仍然保持尖锐.可见,粒子水平集方法较好地解决了传统水平集方法造成的质量、体积与界面细节特征丢失的缺陷,极大地提高了水平集方法的精度.
|
图 2 旋转2π后水平集方法计算结果(a)及粒子水平集方法计算结果(b) Fig. 2 Level set solution after 2π revolution (a) and particle level set solution after 2π revolution (b) |
不可压缩黏性流动控制方程组不是双曲型的,但是CE/SE算法一般只适用于具有双曲型性质的高速流动.文献[16]对不可压缩黏性流动控制方程组进行了预处理,使方程具有双曲型性质,提出了一种新的适用于CE/SE算法的物理时间处理方法.本文采用人工压缩法耦合方程(1)中的速度和压力[16, 23],依据压力分离法,对动量方程进行时间算子分离[24],采用时空守恒元/解元(CE/SE)方法求解[16].其中,虚拟时间采用一阶向前差分,同时引入内迭代.为了避免不合理的压力漂移现象,本文采用半交错网格[14],其中压力定义在网格中心,速度定义在网格的四角.
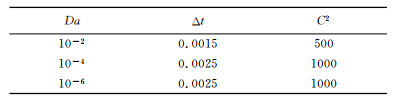
达西数是影响孔隙介质多相流数值收敛速度及稳定性的关键参数,本文实际计算结果得出不同达西数情况下,时间步长Δt和人工压缩系数C2的取值(表 1).
|
|
表 1 计算参数 Table 1 Calculation coefficients |
CE/SE方法将时间和空间统一起来求解,利用守恒型积分方程,通过定义守恒元和解元使得局部和全局都严格满足守恒律,将网格点物理量及其偏导数作为变量同时求解,计算精度高、格式构造简单[10, 25].不同的守恒元和解元的定义可以导出不同的差分格式.本文采用文献[11, 14~16]提出的六面体划分方案,在每个解元上只设置一个守恒元,利用相邻的不同时间半层解元的公共点上的流动变量连续条件导出流动变量及其空间偏导数之间的关系[11].网格点在时间方向的投影、解元与守恒元的具体构造过程参见文献[16].
6 应用 6.1 溃坝流问题计算本文以溃坝流[26]为例,验证提出的孔隙介质中多相流动的CE/SE计算方案.矩形水槽底部长5L、壁高2.5L.初始时刻用挡板在水槽左侧截取高为2L、长为L的水柱,其余部分与空气接触,挡板突然抽出之后,水柱将坍塌并沿水槽底部向前流动,水与背景流体的密度比为1000,黏性比为100[26].
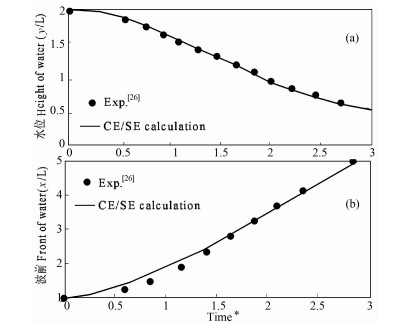
计算中取L=0.057 m[26],ϕ=0.9,Da=104,模型的出口边界为纽曼边界条件,其他边界为速度滑移壁面边界条件.本文模拟了各个时刻的水面最高位置(左侧壁面)和波前位置(水槽底部),并同文献[26]的实验结果进行对比.图 3a为最高水位随无量纲时间(Time*)的变化,图 3b为波前位置随时间的变化,二者与实验结果都符合得很好,说明了本文计算方案的正确性和准确性.
|
图 3 左壁面(a)与下壁面(b)处波前的位置历时演变 Fig. 3 History of water front location on solid surface at the left wall (a) and bottom wall (b), respectively |
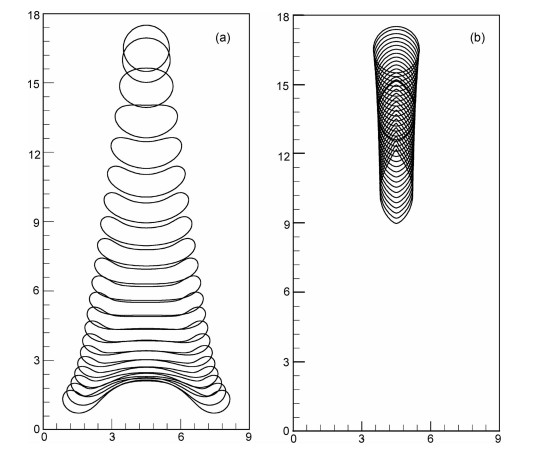
文献[27]采用投影法模拟了液滴在重力作用下的运动与变形,提出了可变时间步长法对水平集函数重新初始化的改进,将水平集方法的质量丢失减小到0.5%.本文将其物理问题概化为一端封闭的管道中充满完全饱和的孔隙介质,考察液滴在重力和表面张力作用下的运动与变形.重点考查孔隙度对液滴运动的影响.管道顶部为自由面边界,管道的左、右及底部是无滑移固体壁面.图 4所示为不同时刻液滴变形历史过程.图中的运动和变形过程是从0时刻到100时刻每5个无量纲时间标记一个液滴状态.
|
图 4 液滴变形运动过程 初始位置(4.5,16.5),密度比λρ=1.125,黏性系数比λμ=50,Re=100,We=50,(a)ϕ=0.9,Da=104;(b)ϕ=0.1,Da=10-2.横纵坐标为无量纲长度. Fig. 4 History of motion and deformation of droplets falling for λρ=1.125, λμ=50, Re=100, We=50 with initial position (4.5, 16.5). (a)ϕ=0.9, Da=104;(b)ϕ=0.1, Da=10-2. |
图 4a显示ϕ=0.9,Da=104的情况下液滴下落过程,随着液滴的下落,液滴逐渐被压扁,液滴底部距离管道底部5.0左右,液滴左右两端开始向下弯折,中部的流体流向两端,两端下降速度逐渐加快,计算结果与文献[27]一致.图 4b显示φ=0.1,Da=10-2的情况下液滴下落过程.随着液滴的下落,液滴逐渐被拉伸,由椭圆形变为纺锤形,液滴底部到达15.0左右,液滴纵向变形增强,上端开始向中部收缩,两侧的流体流向底部,底部下降速度逐渐加快.
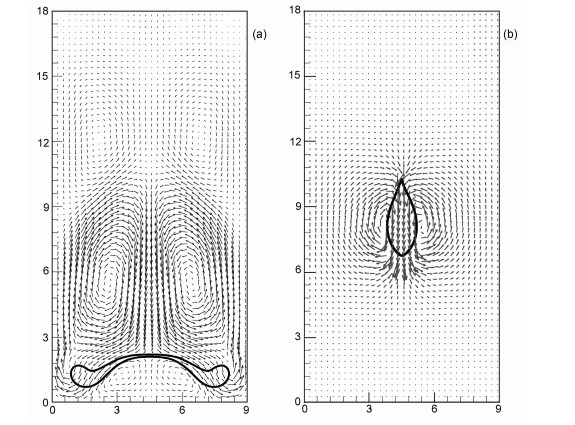
图 5(a,b)给出100时刻流场速度矢量分布,液滴下降过程中激发的流场呈对称分布.图 5a显示ϕ=0.9,Da=104的情况下,在5.0处形成两个对称主涡.图 5b显示ϕ=0.1,Da=10-2的情况下,在8.0处形成两个对称主涡.
|
图 5 100时刻速度矢量 初始位置(4.5,16.5),密度比λρ=1.125,黏性系数比λμ=50,Re=100,We=50,(a)ϕ=0.9,Da=104;(b)ϕ=0.1,Da=10-2.横纵坐标为无量纲长度. Velocity vector at time=100, forλρ=1.125, λμ=50, Re=100, We=50 with initial position (4.5, 16.5).(a)ϕ=0.9, Da=104, (b)ϕ=0.1, Da=10-2. |
从图 5可以看出,随着孔隙度减小,液滴下降速度减慢,下降深度降低,两端变形减弱,底端变形由上凸变为下凸,由两端变形起主导地位到底端变形占优势.孔隙度减小导致达西摩擦和孔隙格架对液体的拖拽作用增强(惯性因子增大),流动的惯性减弱,液滴的运动与变形被约束.揭示了孔隙度对液滴变形和运动的影响.
6.3 孔隙介质双层流体顶盖驱动方腔流本文提出了一个新的孔隙介质两相流物理模型---双层流体顶盖驱动方腔流.双层流体方腔流与常规的单相流体方腔流[16]具有类似的流型.双层流体方腔流既可以提供精确的流线分布又可以提供精确的界面信息,具有规则的几何形状和简单的边界条件.在一定程度上填补了孔隙介质两相流动验证模型的空白,也为其他两相流数值方法提供了一个新的验证模型.
饱和孔隙介质方腔中充满互不相溶的两种液体,二者界面位于方腔中部.为了保证其稳定性,密度较小的流体置于方腔上部,密度较大的流体置于方腔下部.方腔垂直放置,重力作用于整个流体系统.
本文采用高精度CE/SE算法结合粒子水平集函数计算了不同参数下的方腔流动.计算均采用100×200均匀网格.首先计算Re=100,We=50,Fr=1,ϕ=0.2,Da=102时的情况.
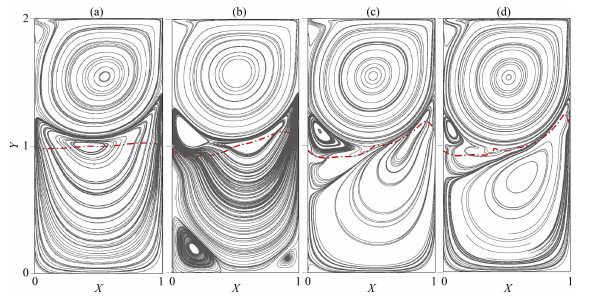
方腔内流动随时间发展变化如图 6(a~d)所示.图中虚线表示两相流界面,实线为流线.初始时刻界面位于方腔的水平中心线上,顶盖拖动上层液体流动后带动整个方腔内流体流动.T=50时刻在右上角发展出一个角涡,现象与单相顶盖驱动方腔流动[16]基本一致.下层液体在界面张力的作用下也形成了一个中心涡,此时流型类似于两个单相方腔流叠加,形成了双层方腔流动的基本流型;由于界面处垂直流速很小,界面位置变化很小.
|
图 6 达西数为102条件下界面与流线的变形演化 (a)50时刻;(b)100时刻;(c)150时刻;(d)200时刻. Fig. 6 Revolution of the interface and stream lines at time of (a) 50, (b) 100, (c) 150, (d) 200, respectively, for Darcy number 102 and viscosity ratio 50 |
随着时间发展,界面效应逐渐显露出来,T=100时刻下层液体在表面张力的作用下形成三个关联涡,流线逐渐平行于界面;同时界面位置也在流动中发生变化,左侧降落,右侧上升.上层的左下角形成一个二级次涡.下层主涡向右上方偏移.上层液体剪切界面诱发的次生涡越来越明显,下层流体的左下角和右下角也同时出现了相对应的次涡;界面在上层流体次涡剪切下反方向移动,此时界面位置右侧比左侧略高.界面有类似于固壁的作用,在雷诺数较大时,会在上层左下角首先“搓起”次生涡.
T=150刻时下层液体在界面张力的作用下形成的中心涡完全偏移到右上角,下层的次涡消失.T=200刻时上层液体左下角已经出现的次涡强度减弱;同时界面也在不断调整位置,让流动趋于稳定,整个区域达到稳定状态,流线与界面完全平行,界面不再变化;上层液体形成一个主涡和两个次生涡,下层流体形成一个主涡.
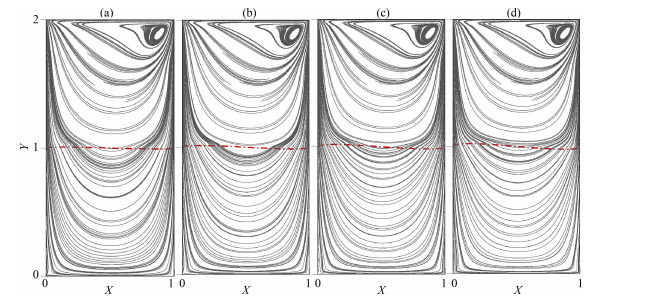
本文同时计算了Da=0.25与Da=0.01下的流型如图 7、8所示.Da=0.25时流动较慢(图 7),剪切能量完全被界面运动消耗,流体在界面上难以“搓起”次生涡,上层流体只在中心右上侧形成一个主涡.由于没有形成次涡,界面处没有反向的剪切力,因此界面的最终形态为左侧偏上右侧偏下,下层流体未能形成一个主涡.
|
图 7 达西数为0.25条件下界面与流线的变形演化 (a)50时刻;(b)100时刻;(c)150时刻;(d)200时刻. Fig. 7 Revolution of the tnterface and stream lines at time of (a) 50, (b) 100, (c) 150, (d) 200, respectively, for Darcy number 0.25 and viscosity ratio 50 |
|
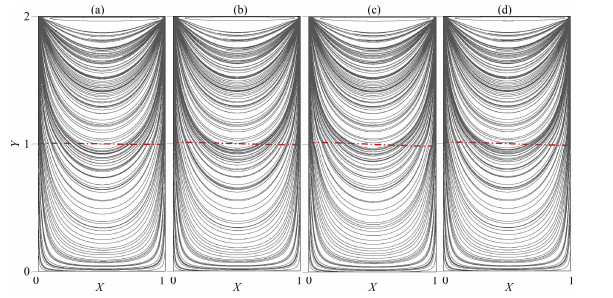
图 8 达西数为0.01条件下界面与流线的变形演化 (a)50时刻;(b)100时刻;(c)150时刻;(d)200时刻. Fig. 8 Revolution of the tnterface and stream lines at time of (a) 50, (b) 100, (c) 150, (d) 200, respectively, for Darcy number 0.01 and viscosity ratio 50 |
Da=0.01时流动更慢(图 8),剪切能量完全被界面运动消耗,界面上未能产生次生涡,上层流体只在中心形成一个主涡,界面几乎保持水平.以上计算表明,双层流体顶盖驱动方腔流的流态主要受达西数的控制.
7 结语本文将时空守恒元解元方法成功地推广到孔隙介质多相流动计算中.同时,结合杂交粒子水平集方法,提出一种有效且精度较高的带有精确界面处理的欧拉型的孔隙介质多相流计算方案.计算中考虑了孔隙介质对流体的拖拽作用以及表面张力的影响.这套计算方案可以方便地处理复杂的物质界面问题.对溃坝流问题、液滴在重力作用下的运动与变形和孔隙介质双层流体顶盖驱动方腔流动等问题进行数值模拟,并把计算结果与有关文献结果进行对比.这是首次采用时空守恒方法成功模拟孔隙介质多相流动.结果表明,CE/SE方法精度较高,物理概念清晰,能够在数值模拟孔隙介质多相流方面得到广泛应用.
致谢审稿专家对本文提出了建设性的修改意见,在此表示感谢!
| [1] | ChangY B, Lim M T, PopeG A, et al. CO2 flow patterns under multiphase flow: field-scale conditions. SPE Reserv.Enf , 1994, 9: 208-216. DOI:10.2118/22654-PA |
| [2] | Gallo Y L, Trenty L, Michel A, et al. Long-term flow simulations of CO2 storage in saline aquifer. In: Proceedings of GHGT-8 8th International Conference on Greenhouse Gas Control Technologies, Norway:Trondheim, 2006. 284 |
| [3] | Vafai K. Convection flow and heat transfer in variable porous media. J.Fluid Mech. , 1984, 47: 233-259. |
| [4] | Reis N C, Griffiths R F, Santos J M. Numerical simulation of the impact of liquid droplets on porous surfaces. J.Compul Phys. , 2004, 198: 747-770. DOI:10.1016/j.jcp.2004.01.024 |
| [5] | Xu X F, Chen S Y, Zhang D X. Convective stability analysis of the long-term storage of carbon dioxide in deep saline aquifers. Advances Resources , 2006, 29: 397-407. DOI:10.1016/j.advwatres.2005.05.008 |
| [6] | Karim M F, Tanimoto K, Hieu P D. Modelling and simulation of wave transformation in porous structures using VOF based two-phase flow model. Applied Mathematical Modelling , 2009, 33: 343-360. DOI:10.1016/j.apm.2007.11.016 |
| [7] | Costa V A F, Oliveira L A, Figueiredo A R. A control volume based finite element method for three-dimensional incompressible turbulent fluid flow, heat transfer, and related phenomena. Int.J.Numer Methods Fluids , 1995, 21: 591-615. DOI:10.1002/(ISSN)1097-0363 |
| [8] | Alkam M K, Alnima M A. Transient non-Darcian forced convection flow in a pipe partially filled with a porous material. Int.J.Heat Mass Transfer , 1998, 41(2): 347-356. DOI:10.1016/S0017-9310(97)00146-4 |
| [9] | Aarnes J E, Kippe V, Lie K A. Mixed multiscale finite elements and streamline methods for reservoir simulation of large geomodel. Adv Water Res. , 2005, 28: 257-271. DOI:10.1016/j.advwatres.2004.10.007 |
| [10] | Chang S C. The method of space-time conservation element and solution element-a new approach for solving the Navier-stokes and Euler equations. Journal of Computational Physics , 1995, 119: 295-324. DOI:10.1006/jcph.1995.1137 |
| [11] | 张德良, 谢巍, 郭长铭, 等. 气相爆轰胞格结构和马赫发射数值模拟. 爆炸与冲击 , 2001, 21(3): 161–167. Zhang D L, Xie W, Guo C M, et al. Numerical simulation of cellar structures and mach reflection of gaseous detonation waves. Explo.Shock Wave (in Chinese) , 2001, 21(3): 161-167. |
| [12] | 王景焘, 张德良, 刘凯欣. 基于CE/SE方法的二维Euler型多物质流体弹塑性问题计算. 计算物理 , 2007, 24(4): 395–401. Wang J T, Zhang D L, Liu K X. A eulerian approach based on CE/SE method for 2 D multimaterial elastic-plastic flows. Chinese Journal of Computational Physics (in Chinese) , 2007, 24(4): 395-401. |
| [13] | Wang G, Zhang D L, Liu K X. An improved CE/SE scheme and its application to detonation propagation. Chin.Phys.Lett , 2007, 24(2): 3563-3566. |
| [14] | Wang J, Liu K X, Zhang D L. An improved CE/SE scheme for multi-meterial elastic-plastic flows and its application. Computers & Fluids , 2008, 38(3): 544-551. |
| [15] | 张德良, 王景焘, 王刚. 髙精度CE/SE算法及应用. 计算物理 , 2009, 26(2): 211–220. Zhang D L, Wang J T. High-oder CE/SE method and applications. Chinese Journal of Computational Physics (in Chinese) , 2009, 26(2): 211-220. |
| [16] | Yang D X, Li G M, Zhang D L. A CE/SE scheme for flows in porous media and its application. Aerosol Air Qual.Res , 2009, 9(2): 266-276. |
| [17] | Maša P, Steven L B. A level set method for determining critical curvatures for drainage and imbibition. Journal of Collid and Itnerface Science , 2006, 304: 442-458. DOI:10.1016/j.jcis.2006.08.048 |
| [18] | Enright D, Fedkiw R, Ferziger J. A hybrid Particle Level Set method for improved interfaces capturing. Journal of Computational Physics , 2002, 176: 205-227. DOI:10.1006/jcph.2001.6977 |
| [19] | Brackbill J U, Kothe D B, Zemach C. A continuum method for modelling surface tension. J.Comput.Phys. , 1992, 100: 35-354. |
| [20] | Osher S, Sethian J A. Fronts propagating with curvatute-dependent speed: Algorithms based on Hamilton-Jacobi formulations. Journal of Computational Physics , 1988, 79: 12-49. DOI:10.1016/0021-9991(88)90002-2 |
| [21] | Jiang G S, Peng D. Weighted ENO schemes for Hamilton-Jacobi equations. SIAM Journal on Scientific Computing , 2000, 21: 2126-2143. DOI:10.1137/S106482759732455X |
| [22] | Prodanovic M, Bryant S L. A level set method for determining critical curvatures for drainage and imbibition. Journal of Colloid and Interface Science , 2006, 304: 442-458. DOI:10.1016/j.jcis.2006.08.048 |
| [23] | Chorin A J. Numerical solution of the Navier-Stokes equations. Mathematics of Computation , 1968, 22: 745-762. DOI:10.1090/S0025-5718-1968-0242392-2 |
| [24] | Jue TC. Analysis of oscillatory flow with thermal convection in a rectangle cavity filled with porous medium. Int.Comm.Heat Mass Transfer , 2000, 27(7): 985-994. DOI:10.1016/S0735-1933(00)00178-0 |
| [25] | Chang S C, Wang X Y, Chow C Y. The Space-time conservation element and solution element method: a new high-resolution and genuinely multidimensional paradigm for solving conservation laws. Journal of Computational Physics , 1999, 156: 89-136. DOI:10.1006/jcph.1999.6354 |
| [26] | Martin J C, Moyce W J. An experimental study of the collapse of liquid columns on a rigid horizontal plane. Philos.Trans.Roy.Scc.Lond.Ser.A-Math.Phys.Sci. , 1952, 244(882): 312-324. DOI:10.1098/rsta.1952.0006 |
| [27] | Ni M J, Komori S, Morley N B. Direct simulation of falling droplet in a closed channel. Int.J.Heat Mass Transfer , 2006, 49: 366-376. DOI:10.1016/j.ijheatmasstransfer.2005.03.025 |
 2010, Vol. 53
2010, Vol. 53