长期以来,人们一直在探索研究地层浅部地电构造勘探的有效方法,以寻找各种矿产资源以及解决各种水文地质工程问题.在众多的地球物理探测方法中,电法勘探由于其场源的多变性、方法的多样性及解决问题的有效性,已越来越为世人所关注.而其中的人工源频率域电磁方法,由于具有工作效率高、信号强度大、分辨能力好等优点而成为电法勘探中的一个重要分支.人工源频率域的电磁方法又可以分解为多种具体的勘探方法,例如可控源音频大地电磁法、极低频探地电磁法、海洋可控源电磁法等.
在20世纪70年代提出的可控源音频大地电磁法(CSAMT)是在大地电磁法(MT)的基础上发展起来的一种人工源频率域电磁测深方法.人们对其进行了大量的理论及应用研究,方法已经在煤田、找矿、地热、工程等方面得到了广泛的应用,成为一种不可或缺的电磁勘探手段[1~9].但是它也存在着探测深度较浅,源的野外布设较麻烦等缺点.这些缺点是方法本身所固有的,这使得很多情况下此方法都不再满足人们的需求.于是结合了MT与CSAMT两者优点的人工源极低频探地电磁法(WEM)应运而生.WEM方法是通过在地表铺设几十公里长的电缆源,用大功率发电机发射电磁波,在全国大部分范围进行信号的接收而进行地下探测的一种新方法[10~12].
近年来应用在海洋中的海洋可控源电磁法(Marine CSEM,简称MCSEM)发展迅速.此方法在20世纪70年代被提出时并没有受到太多的关注.但在发现它对水平高阻层具有较高分辨力的优点后,人们把它广泛应用到了海洋油气的探测之中,从而使方法得到了快速的发展[13~28].
在进行上述各种方法的研究时,人们往往是孤立地去分析某种具体的方法,而较少将问题结合起来进行综合研究,这导致了对方法研究的不完善,一种方法的研究成果很难直接应用到另一种方法之中.
我们可以将这些人工源频率域电磁法的正演问题均简单地抽象为同一类的一维模型正演问题,即抽象为在水平层状介质中,将源置于介质内部(内源模式)或者介质边部(外源模式)某位置提供电磁信号,在其他位置进行信号接收的模型.为了找到此模型统一的正演解决方案,本文在建立的模型基础上进行了电磁场传播规律的分析,以水平电偶源为例进行了电磁场正演理论公式的推导,给出了详细的计算层状介质中任意位置电磁场值的理论计算公式.因为文中定义的层矩阵是建立起层关系的关键,所以称此方法为层矩阵法.层矩阵法的核心是对空间域中变量x,y,z中的x和y变量进行傅氏变换转换到波数域kx和ky中,在波数域利用边界条件用层矩阵建立起各层参数之间的关系后计算得到各层的波数域电磁场值,然后经过二维反傅氏变换运算最终得到空间域中任意位置的场值.层矩阵法理论上可以计算任意层状介质中任意位置的任意场源在空间中任意位置产生的场强,可适用于多种人工源频率域电磁法的正演模拟计算.
文中在给出水平电偶源层矩阵法的完整推导公式后,为了考察其计算的可靠性,随后计算给出了波数域中它与文献解析解的对比,然后在空间域给出了无限均匀介质模型时与文献解析解的对比,以及分别在均匀大地及H、K、A、Q型大地模型与经典CSAMT解法的对比.通过对比分析给出了层矩阵法的优点与不足,并提出了将来需要进一步解决的问题.
2 理论公式推导 2.1 理论模型及场满足的微分方程
建立模型如图 1,在第0层中有一个距底界面高度为h,长度为ds的水平电偶极子,其中电流为I=I0eiωt,电偶极距为pE=Ids.坐标原点位于电偶源正下方的z1界面上,竖直向下为z轴的正方向.第0层的上方有M层介质,下方有N层介质.各层的阻抗率
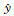
|
图 1 层矩阵法模型 Fig. 1 The sketch of layer-matrix model |
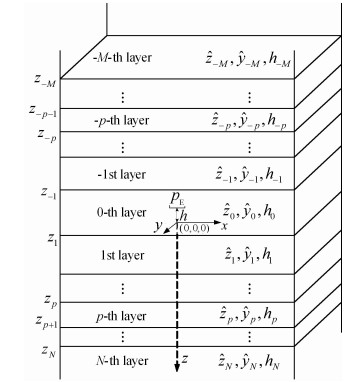
首先定义二重傅氏变换对:
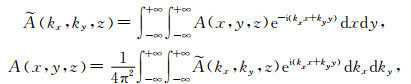
|
(1) |
式(1)表明空间域(x,y,z)与波数域(kx,ky,z)中的值是可以相互转换的,联系两者的是二重傅氏变换对.如果可以得到波数域中的值,便可以通过(1)式的下式获得空间域中的值.
为了理论推导的方便,对x和y两个方向分别进行傅氏变换,令它们进入到变换域中,这样就使三维的空间域问题变成了一维问题,便可以方便地采用层矩阵法获得全空间层状介质的电磁场理论解.
对于层状介质空间中一个电性源,引入Schelkunoff势A,它满足如下的Helmholtz方程[29]:
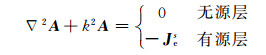
|
(2) |
其中,Jes为电流密度,k为层的波数,当采用正谐时,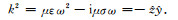
电场和磁场可以由A通过下式得到
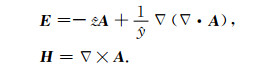
|
(3) |
则x方向的电场和y方向的磁场为
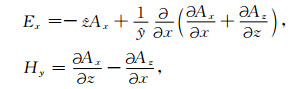
|
(4) |
转换到波数(kx,ky,z)域中,利用傅氏变换的性质,可得
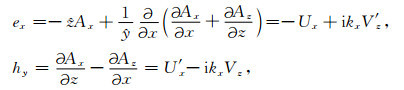
|
(5) |
其中,
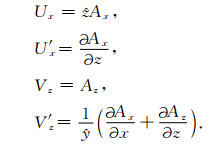
|
(6) |
从(5)式可以看出,只要得到z为任意值时的Ux,U'x,Vz,V'z4个参数,便可求得波数域中的场值,再经过x和y方向的二维反傅氏变换计算即可得到空间域中任意位置的场值.于是最主要的问题就成为如何求解Ux,U'x,Vz,V'z4个参数.
2.2 边界条件在层与层的界面zp上,空间域中的Schelkunoff势A满足如下的关系[29]:
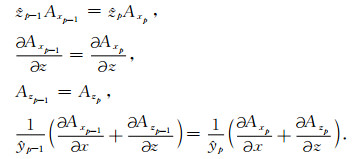
|
(7) |
由于傅氏变换为线性的积分变换,所以上述的边界条件在波数(kx,ky,z)域中是成立的.于是,在波数域中的zp边界上有:

|
(8) |
对于无源层,采用(2)式的上式,因一次源是沿x轴方向的,由成层介质的对称性可以得到Ay=0,公式(2)的上式可以简化为
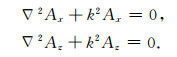
|
(9) |
式(9)为空间域内的齐次Helmholtz方程,变换到(kx,ky,z)域内可以得到
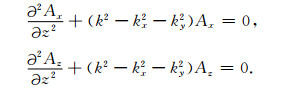
|
(10) |
因为k2=kx2+ky2+kz2,所以
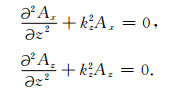
|
(11) |
式(11)为(kx,ky,z)域中的齐次Helmholtz方程,其通解为
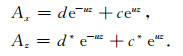
|
(12) |
其中,d,c,d*,c*为第p层的待定系数,u=ikz=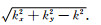
将式(12)代入式(6)可得
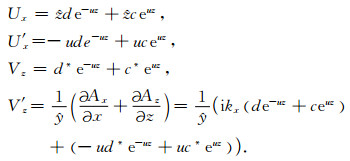
|
(13) |
有源层中,采用(2)式的下式,对于层状介质的x方向电偶极子的情况,特解只有x分量,其满足的方程可简化为
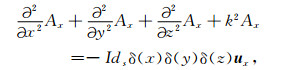
|
(14) |
方程(14)的特解为[29]
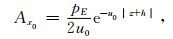
|
(15) |
其中,h为源的高度.
特解加上通解即得到有源层的解:
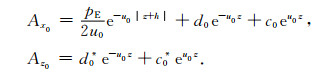
|
(16) |
其中,d0,c0,d0*,c0*为第0层的待定系数.将上式代入(6)式可得
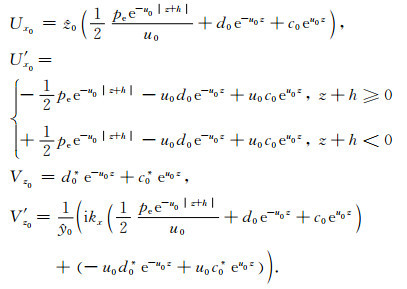
|
(17) |
对于第N层,因为z为正值,所以式(12)中的c,c*须为零,则
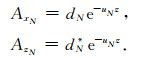
|
(18) |
代入(6)式可得
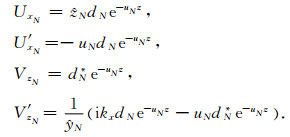
|
(19) |
对于第-M层,因为z为负值,所以(12)式中的d,d*须为零,则
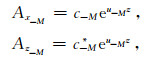
|
(20) |
代入式(6)可得
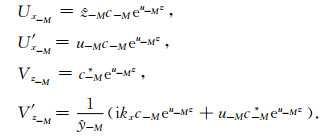
|
(21) |
对于无源的第p层,有
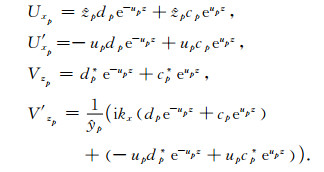
|
(22) |
写成矩阵形式为
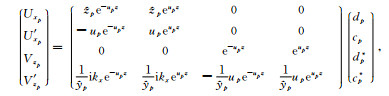
|
(23) |
在第p层的底界面,即z=zp+1上
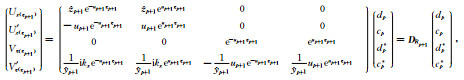
|
(24) |
其中
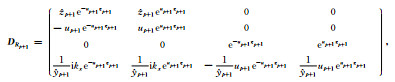
|
(25) |
在第p层的顶界面,即z=zp上有
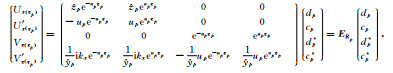
|
(26) |
其中
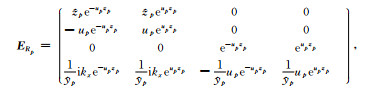
|
(27) |
所以
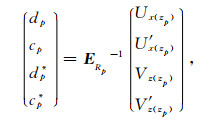
|
(28) |
将(28)式代入(24)式中,得
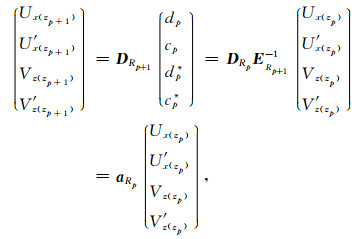
|
(29) |
也可以写成
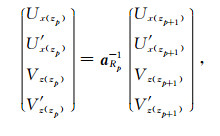
|
(30) |
其中aRp=DRp+1ERp-1,称为第p层层矩阵.式(29)表明第p层底界面的值可以用第p层顶界面的值表示,联系两者的是层矩阵aRp.式(30)表明第p层顶界面的值可以用第p层底界面的值表示,联系两者的是层矩阵的逆矩阵aRp-1.
于是,在第0层的底界面,即z=z1上,
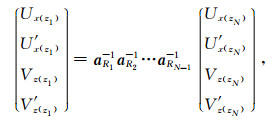
|
(31) |
而在第0层的顶界面,即z=z-1上,
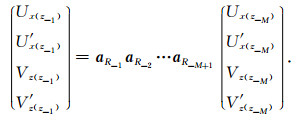
|
(32) |
式(32)与式(31)为最终得到的利用层矩阵aRp及其逆矩阵aRp-1分别建立起的最上层(第-M层)和最下层(第N层)与第0层的关系.而由式(17)、(19)、(21)可知,此关系实际是建立起了d0,c0,d0 *,c0 *分别与dN,dN*和c-M,c-M*的关系,于是利用d0,c0,d0*,c0*作为中间媒介,就可建立起dN,dN*与c-M,c-M*的关系.当各层的电性参数和几何参数确定后,层矩阵就是已知的,所以建立起的4个关系式中仅包含了dN,dN* N和c-M,c-M*共4个未知数,从而可以惟一求解得到这4个参数.然后利用式(19)和式(21)便可得到第N层的UxN,U'xN,VzN,V'zN和第-M层的Ux-M,U'x-M,Vz-M,V'z-M.再利用各层的层矩阵根据(29)或(30)式便可逐层得到z为任意值时的Ux,U'x,Vz,V'z.然后根据(5)式即可求出波数(kx,ky,z)域中的ex和hy,得到的波数域中的结果再用式(1)的下式进行二维傅氏反变换即可最终得到空间域中任意位置的场值.
3 方法可靠性验证为了验证方法的可靠性,本文进行了多种模型的层矩阵法与现有解析公式解的对比分析.按照由简单到复杂的原则,首先在波数域中与文献[29]中的解析解进行了对比,在验证了波数域层矩阵法结果的正确性后进行了空间域中的对比分析.在无限均匀介质模型时与解析公式的解进行对比之后,分别建立了CSAMT方法的均匀、H型、K型、A型、Q型大地模型,将层矩阵法与常用经典的CSAMT解析公式的解进行了对比.
程序中所有水平电偶源均位于原点,令其电偶极距pE=1.在波数域转换到空间域的过程中采用了快速二维反傅氏变换算法,采用的参数均为x方向采样间隔dx=500m,采样点数Nx=512,y方向采样间隔dy=50m,采样点数Ny=4096.图中的虚线为层矩阵法的计算结果,实线为各种模型解析公式的计算结果.
3.1 波数域中的对比按照文献[29]给出的公式进行推导,可以得到,对于层状大地上的水平电偶源,偶极与大地之间的波数(kx,ky,z)域解析式为
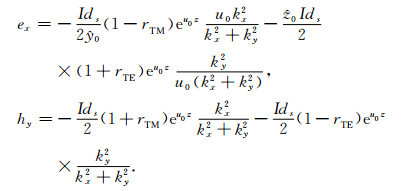
|
(33) |
当大地为均匀介质时,
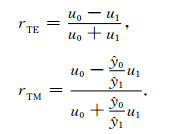
|
(34) |
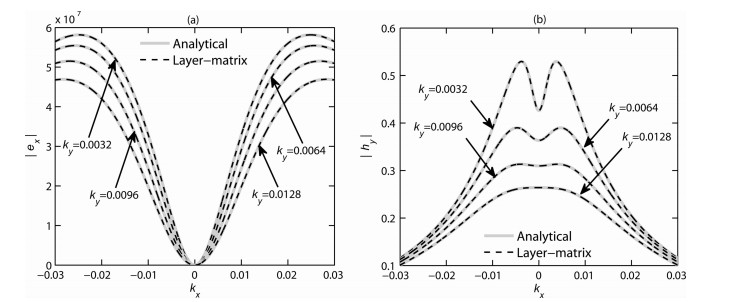
为了与此解析解进行对比,建立了两层介质模型,即第0层和第1层的厚度均为无穷大,电阻率分别为1014 Ωm和1000 Ωm.源的高度h=100 m,频率f=1 Hz,计算了z=-50 m(第0层中)的波数域场强.文中给出了当ky分别为0.0032、0.0064、0.0096和0.0128时随kx变化的层矩阵法与上述解析解的计算结果对比曲线,如图 2所示.
|
图 2 波数域层矩阵法与解析解对比 (a)波数域电场ex;(b)波数域磁场hy. Fig. 2 Comparison of layer-matrix and analytical solutions in wave number domain |
可以看到,对于任意的波数kx和ky,层矩阵法与解析公式的计算曲线均完全重合在了一起,两者的计算结果完全相等,这表明层矩阵法对此模型计算得到的波数域的场是毫无问题的.因为未找到波数域其他位置(其他z值)场的文献,所以下面将进行空间域中的对比分析.
3.2 空间域中的对比 3.2.1 无限均匀介质模型按照文献[29],对于无限均匀介质,在忽略位移电流的情况下,电场和磁场的解析解为
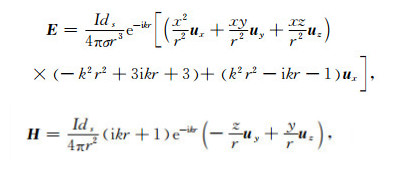
|
(35) |
其中r为所求的点到原点的距离.
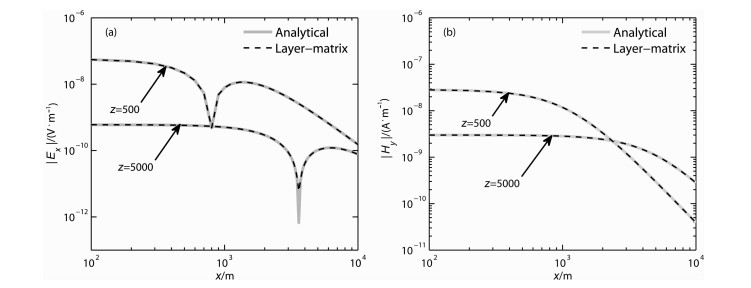
为了与此公式进行对比,建立了电阻率为1000 Ωm的无限均匀介质模型.源的高度h=0 m,频率f=0.1Hz,计算给出了z分别为500 m和5000 m的平面上y为1000m时的电磁场强随x的变化曲线对比(如图 3所示).
|
图 3 无线均匀介质模型的层矩阵法与解析解对比 (a)电场Ex;(b)磁场Hy. Fig. 3 Comparison of layer-matrix and analytical solutions for homogeneous medium model |
从图中可以看到,层矩阵法与解析解的计算曲线基本完全重合.说明对此简单模型,层矩阵法得到的空间域中的结果是正确的.
3.2.2 均匀大地模型按照文献[30],对于水平电偶源位于均匀大地表面的情况,如果采用负谐,将方程形式写为▽2A-k2A=0并令空气中的k0=0时,在z≤0,即地表和大地中空间域的矢量位表达式为
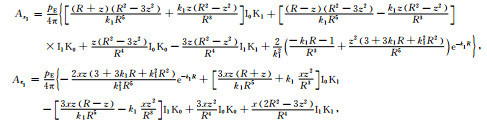
|
(36) |
其中,R为所求位置到原点的距离,大地中的波数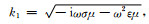
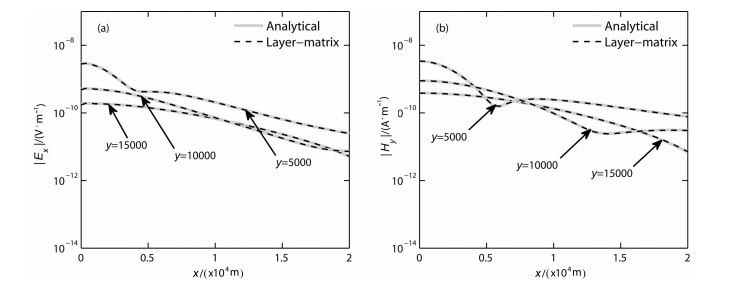
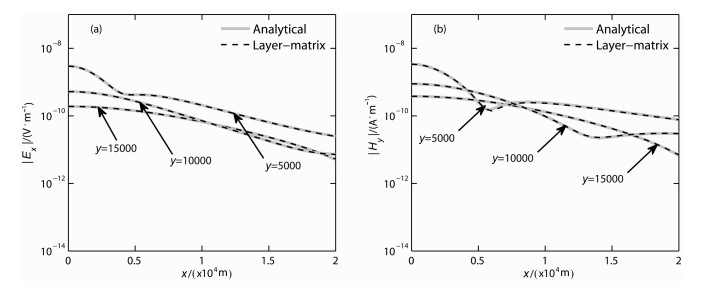
为与此公式解进行对比,建立了均匀大地模型,即第0层和第1层的厚度均为无穷大,电阻率分别为1014 Ωm和2000 Ωm.源的高度h=0m,频率f=10Hz,计算了z为0m(第0层中)和100m(第1层中)的平面上,y分别为5000m、10000m和15000m的场值随x的变化曲线,如图 4和图 5所示.
|
图 4 均匀大地模型层矩阵法与解析公式解对比(z=0m) (a)电场Ex;(b)磁场Hy. Fig. 4 Comparison of layer-matrix and analytical solutions for homogeneous earth model (z=0 m) |
|
图 5 均匀大地模型的层矩阵法与解析公式解对比(z=100 m) (a)电场Ex;(b)磁场Hy. Fig. 5 Comparison of layer-matrix and analytical solutions for homogeneous earth model (z=100 m) |
分析图 4和图 5可以看到,对于电场Ex和磁场Hy,无论z为0 m还是100 m,层矩阵法的计算结果与解析解均比较一致.
3.2.3 大地分层模型为了考察大地水平分层模型时层矩阵法的可靠性,下面分别进行了H、K、A、Q型大地分层模型时层矩阵法与经典CSAMT解析公式解的对比分析.计算采用了代表空气层的第0层和代表大地层的1至3层共4层的模型,第0层至第3层的厚度分别为无穷大、300m、600m和无穷大.给出了h=0m,z=0m(第0层中)即源与接收均位于地表时y分别为5000m、10000m和15000m的场值随x的变化对比曲线.
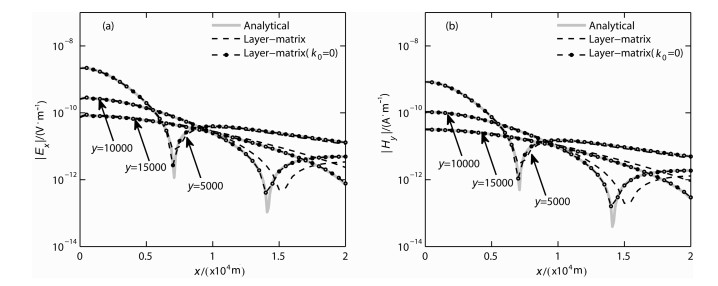
图 6与图 7是H型分层大地模型的计算结果,模型中第0层至第3层的电阻率分别为1014 Ωm、1000 Ωm、250 Ωm和4000 Ωm.图 6给出的是频率f=100 Hz时的情况,可以看到此时两者的计算结果是比较一致的.但是当频率升高到1000 Hz,如图 7所示,在收发距较远(即x或y较大)时,层矩阵法与解析公式计算所得到的结果相差较多,而且随着收发距的增加这种差别越来越大.经过分析认为这是由于空气层的波数影响所造成的.在层矩阵法的推导中严格考虑了所有层的波数,而经典CSAMT解析公式是在假设空气中波数为0的情况下推导得到的,并没有考虑到空气中波数的影响.当频率较低时,这种假设基本成立,而随着频率的升高,空气中波数的影响逐渐增大.在本例中空气层的波数实际为:
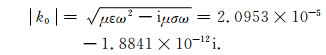
|
(37) |
|
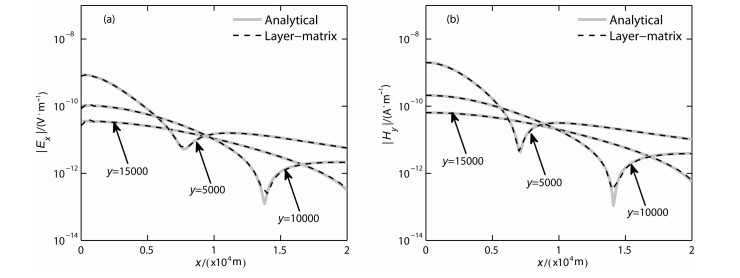
图 6 层矩阵法与解析公式解对比(H型,f=100 Hz) (a)电场Ex;(b)磁场Hy. Fig. 6 Comparison of layer-matrix and analytical solutions (H model, f=100 Hz) |
|
图 7 层矩阵法与解析公式解对比(H型,f=1000 Hz) (a)电场Ex;(b)磁场Hy. Fig. 7 Comparison of layer-matrix and analytical solutions (H model, f=1000 Hz) |
可以看到根号中实部所代表的位移项使得空气的波数值较大,在计算稍远位置的场值时不应该被忽略,所以再采用经典CSAMT解析公式计算所得的结果肯定是不准确的.图 7中的点虚线为在层矩阵法中将空气中波数值强制置为0时的结果,此时两者结果曲线才基本重合,这也就说明前述两者曲线的分离就是空气的波数所造成的.上述分析表明经典的CSAMT解析公式的应用范围是受限的,所以文后将不再进行高频情况的对比计算.
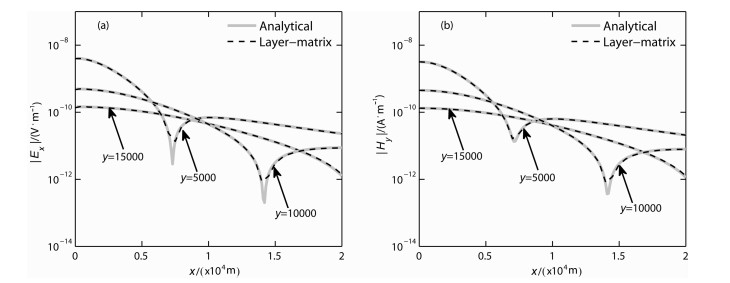
下面分别给出了K型、A型和Q型大地分层模型频率f=100 Hz的层矩阵法与经典CSAMT解析公式的计算结果对比,其中图 8为K型大地分层模型,第0层至第3层的电阻率分别为1014 Ωm、1000、4000 Ωm和1000 Ωm.图 9为A型大地分层模型,第0层至第3层的电阻率分别为1014 Ωm、1000、4000 Ωm和32000 Ωm.图 10为Q型大地分层模型,第0层至第3层的电阻率分别为1014 Ωm、1000、250 Ωm和31.25 Ωm.
|
图 8 层矩阵法与解析公式解对比(K型,f=100 Hz) (a)电场Ex;(b)磁场Hy. Fig. 8 Comparison of layer-matrix and analytical solutions (K model, f=100 Hz) |
|
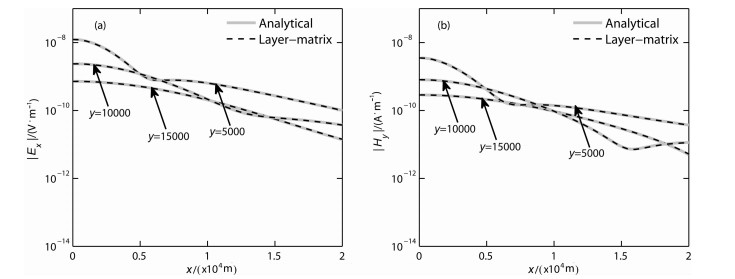
图 9 层矩阵法与解析公式解对比(A型,f=100 Hz) (a)电场Ex;(b)磁场Hy. Fig. 9 Comparison of layer-matrix and analytical solutions (A model, f=100 Hz) |
|
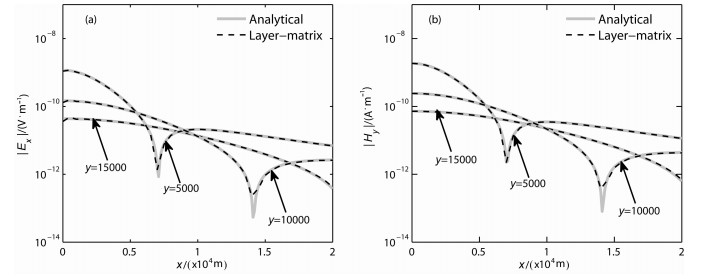
图 10 层矩阵法与解析公式解对比(Q型,f=100 Hz) (a)电场Ex;(b)磁场Hy. Fig. 10 Comparison of layer-matrix and analytical solutions (Q model, f=100 Hz) |
仔细观察各曲线可以发现一些问题,比如各场值曲线的波谷处两者稍有差别.这是层矩阵法x方向采样间隔(dx=500 m)稍大造成的曲线不圆滑,减小采样间隔就可以消除.另外在详细分析各种模型的计算数据后发现,在x=0即y轴附近的位置,不同模型的场值结果均存在着不同程度的震荡现象,其中电场的震荡较明显一些,在曲线图中稍有体现.分析这可能是由于傅氏反变换的计算所导致的,具体原因还需进行更加深入的研究.
从整体上看,对于各种不同的大地分层模型层矩阵法所得的结果都是比较令人满意的.与解析公式计算曲线的基本重合,不仅表明层矩阵法的计算结果是正确的,而且也表明它的计算精度是比较高的.
4 讨论与结论现有文献中各种理论公式及解法大多仅能适用于某种具体的方法,而本文中提出的层矩阵法是在综合多种方法共同点的水平层状介质模型的基础上推导得到的,它可以用来计算任意层状介质中任意位置的任意场源在空间中任意位置产生的场强,既适用于外源模式(如CSAMT),又适用于内源模式(如WEM,MCSEM),可以用来进行多种方法的正演模拟计算.文中给出的是水平电偶源层矩阵法的推导公式,通过修改边界条件,就可以将方法方便地推广到其他形式的源(例如磁源).
文章中建立了多种适合现有解析公式的模型,对比给出了层矩阵法与各种解析公式的计算结果.分析结果表明层矩阵法不仅可以根据要求建立灵活多样的各种模型,而且其计算结果都是正确的,其计算精度都是比较高的.
在分析各种模型的计算结果时也发现了层矩阵法的一些不足,比如在x=0附近场值存在着震荡的现象,这需要对其进行进一步的研究工作.
总之,层矩阵法的计算灵活、可靠,值得对其进行深入地研究与发展.
限于篇幅的关系,本文仅主要给出了层矩阵法在CSAMT方法中的对比,其在MCSEM及WEM等方法中的应用将另文发表.
| [1] | 底青云, 王若. 可控源音频大地电磁数据正反演及方法应用. 北京: 科学出版社, 2008 . Di Q Y, Wang R. Controlled Source Audio-frequency Magnetotelluric Data Forward Modeling, Iinversion and Iits Application (in Chinese). Beijing: Science Press, 2008 . |
| [2] | 何继善. 可控源音频大地电磁法. 长沙: 中南工业大学出版社, 1990 . He J S. Controlled Source Audio-frequency Magnetotelluric Method (in Chinese). Changsha: Central South University of Technology Press, 1990 . |
| [3] | 底青云, 王光杰, 安志国, 等. 南水北调西线千米深长隧洞围岩构造地球物理勘探. 地球物理学报 , 2006, 49(6): 1836–1842. Di Q Y, Wang G J, An Z G, et al. Geophysical exploration of a long deep tunnel on the west route of South to North Water Diversion Project. Chinese J. Geophys (in Chinese) , 2006, 49(6): 1836-1842. |
| [4] | 底青云, 王妙月, 石昆法, 等. 髙分辨V6系统在矿山顶板涌水隐患中的应用研究. 地球物理学报 , 2002, 45(5): 744–748. Di Q Y, Wang M Y, Shi K F. CSAMT research survey for preventing water flooding in mining. Chinese J. Geophys. (in Chinese) , 2002, 45(5): 744-748. |
| [5] | 底青云, UnsworthM, 王妙月. 复杂介质有限元法2.5维可控源音频大地电磁法数值模拟. 地球物理学报 , 2004, 47(4): 723–730. Di Q Y, Unsworth M, Wang M Y, et al. 2.5 D CSAMT modeling with the finite element method over complex earth media. Chinese J. Geophys. (in Chinese) , 2004, 47(4): 723-730. |
| [6] | 底青云, UnsworthM, 王妙月. 有限元法2.5维CSAMT数值模拟. 地球物理学进展 , 2004, 19(2): 317–324. Di Q Y, Unsworth M, Wang M Y. 2.5 D CSAMT modeling with finite element method. Progress in Geophysics (in Chinese) , 2004, 19(2): 317-324. |
| [7] | 王若, 王妙月, 底青云. 频率域线源大地电磁法有限元正演模拟. 地球物理学报 , 2006, 49(6): 1858–1866. Wang R, Wang M Y, Di Q Y. Electromagnetic modeling due to line source in frequency domain using finite element method. Chinese J. Geophys. (in Chinese) , 2006, 49(6): 1858-1866. |
| [8] | 石昆法. 可控源音频大地电磁法理论与应用. 北京: 科学出版社, 1999 . Shi K F. Controllable Source Audio Frequency Magnetotelluric Method Theory and Application (in Chinese). Beijing: Science Press, 1999 . |
| [9] | 汤井田, 何继善. 可控源音频大地电磁法及其应用. 长沙: 中南大学出版社, 2005 . Tang J T, He J S. Controlled Source Electromagnetic Method and Its Applications (in Chinese). Changsha: Central South University Press, 2005 . |
| [10] | 底青云, 王妙月, 王若, 等. 长偶极大功率可控源电磁波响应特征研究. 地球物理学报 , 2008, 51(6): 1917–1928. Di Q Y, Wang M Y, Wang R, et al. Study of the long bipole and large power electromagnetic field. Chinese J. Geophys. (in Chinese) , 2008, 51(6): 1917-1928. |
| [11] | 底青云, 王光杰, 王妙月, 等. 长偶极大功率可控源激励下目标体电性参数的频率响应. 地球物理学报 , 2009, 52(1): 275–280. Di Q Y, Wang G J, Wang M Y, et al. Frequency response characteristics of target electric property with long bipole large power control source. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 275-280. |
| [12] | 卓贤军, 赵国泽, 底青云, 等. 无线电磁法(WEM)在地球物理勘探中的初步应用. 地球物理学进展 , 2007, 22(6): 1921–1924. Zhuo X J, Zhao G Z, Di Q Y, et al. Preliminary application of WEM in geophysical exploration. Progress in Geophysics (in Chinese) , 2007, 22(6): 1921-1924. |
| [13] | Fu C M, Di Q Y, Wang M Y. 3D Numeric emulation of marine controlled source electromagnetic method (MCSEM). Oil Geophysical Prospecting , 2009, 44(Supp. 2): 135-141. |
| [14] | Sinha M C, Patel P D, Unsworth M J, et al. An active source electromagnetic sounding system for marine use. Marine Geophysical Researchs , 1990, 12(1): 59-68. |
| [15] | Chave A D, Cox C S. Controlled electromagnetic sources for measuring electrical conductivity beneath the ocean 1.Forward problem and model study. Journal of Geophysical Research , 1982, 87(B7): 5327-5338. DOI:10.1029/JB087iB07p05327 |
| [16] | Unsworth M J, Travis B J, Chave A D. Electromagnetic induction by a finite electric dipole source over a 2-D earth. Geophysics , 1993, 58(2): 198-214. DOI:10.1190/1.1443406 |
| [17] | Constable S, Srnka L J. An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration. Geophysics , 2007, 72(2): WA3-WA12. DOI:10.1190/1.2432483 |
| [18] | Weiss C J, Constable S. Mapping thin resistors and hydrocarbons with marine EM methods, Part Ⅱ-Modeling and analysis in 3D. Geophysics , 2006, 71(6): G321-G332. DOI:10.1190/1.2356908 |
| [19] | Nabighian M.Electromagnetic Methods in Applied Geophysics, Vol. 2., Application. Tulsa: Society of Exploration Geophysicists, 1991 |
| [20] | Constable S, Cox C S. Marine controlled-source electromagnetic sounding. 2. The PEGASUS experiment. Journal of Geophysical Research , 1996, 101(B3): 5519-5530. DOI:10.1029/95JB03738 |
| [21] | Flosadottir A H, Constable S. Marine controlled source electromagnetic sounding 1. Modeling and experimental design. Journal of Geophysical Research , 1996, 101(B3): 5507-5517. DOI:10.1029/95JB03739 |
| [22] | Edwards N. Marine Controlled Source Electromagnetics: Principles, Methodologies, Future Commercial Applications. Surveys in Geophysics , 2005, 26(6): 675-700. DOI:10.1007/s10712-005-1830-3 |
| [23] | Constable S, Weiss C J. Mapping thin resistors and hydrocarbons with marine EM methods: Insights from 1D modeling. Geophysics , 2006, 71(2): G43-G51. DOI:10.1190/1.2187748 |
| [24] | Alexander G, Michael Z. Rigorous 3 D inversion of marine CSEM data based on the integral equation method. Geophysics , 2007, 72(2): WA73-WA84. DOI:10.1190/1.2435712 |
| [25] | Christensen N B, Dodds K. 1D inversion and resolution analysis of marine CSEM data. Geophysics , 2007, 72(2): WA27-WA38. DOI:10.1190/1.2437092 |
| [26] | 何展翔, 孙卫斌, 孔繁恕, 等. 海洋电磁法. 石油地球物理勘探 , 2006, 41(4): 451–457. He Z X, Sun W B, Kong F S, et al. Marine Electromagnetic Approach. Oil Geophysical Prospecting (in Chinese) , 2006, 41(4): 451-457. |
| [27] | 何展翔, 余刚. 海洋电磁勘探技术及新进展. 勘探地球物理进展 , 2008, 31(1): 2–9. He Z X, Yu G. Marine EM survey technology and its new advances. Progress in Exploration Geophysics (in Chinese) , 2008, 31(1): 2-9. |
| [28] | 付长民, 底青云, 王妙月. 海洋可控源电磁法三维数值模拟. 石油地球物理勘探 , 2009, 44(3): 358–363. Fu C M, Di Q Y, Wang M Y. 3D modeling of Marine CSEM method. Oil Geophysical Prospecting (in Chinese) , 2009, 44(3): 358-363. |
| [29] | Nabighian M N. Electromagnetic methods in applied geophysics (Volume 1, theory). Society of Exploration Geophysicists, 1987 |
| [30] | 朴化荣. 电磁测深法原理. 北京: 地质出版社, 1990 . Piao H R. Principles of Electromagnetic Sounding (in Chinese). Beijing: Geological Publishing House, 1990 . |
 2010, Vol. 53
2010, Vol. 53

