地磁场可分为稳定磁场和变化(瞬变)磁场,而变化磁场又可分为规则变化与不规则变化.K指数作为最常用的一种地磁活动指数,它以3小时为一时段,用0,1,…,9分10级来描述不规则变化的扰动程度[1].由于稳定磁场变化缓慢,对K指数标定的影响可以忽略,因此K指数标定问题的关键是如何在地磁场中消去规则变化(如,太阳静日变化Sq).然而,在不同天和不同地磁活动水平情况下,规则变化的形态和幅度都存在很大差异[2~4].
Bartels等人设计K指数时,指出规则变化(原文中称作非K变化,因为K指数并不描述它)主要包括三部分:太阳静日变化(Sq)、太阴日变化(L)及扰后效应(Dma)[5].其中Sq是最主要的一种规则变化,它存在逐日异变性;而L虽然比较小(幅度只有2~3 nT),它也与月相和季节有关,并非完全规则;至于扰后效应(它是太阳微粒辐射所形成的残留干扰的缓慢恢复过程),较前二者更为复杂.Bartels等人虽然指出了SR的物理基础,却并未给出确定SR的具体方法.Mayaud提出了一系列法则-确定SR的形态学方法[6],并被地磁台站采用,根据磁照图手工标定K指数.K指数计算机标定算法大致可分为四类:滑动窗回归法(如USGS[7]、FMI[8])、有约束回归法(如ASm[9]、BGS[10, 11]、NZ[12])、磁照图滤波法(如ASp [13]、GOT[14]、LRNS[15])和正交向量基分解法(如KMO[16]、MNOC[17]).这些算法争论的焦点在于如何合理地识别SR曲线,文献[18]综述了上述算法,并与手工标定的K指数比较发现FMI法优于其他方法[19].齐玮等[20]修正了FMI方法的一个疏漏,实验表明修正后的FMI方法能够更准确地标定K指数.
然而FMI方法标定K指数有一天的延迟-为了确定当天的SR曲线,需要次日的地磁数据.本文利用径向基神经网络对规则变化SR进行建模,通过模型准确地获取当天的SR曲线,从而给出了一种K指数的实时标定方法.
2 FMI方法及径向基神经网络简介 2.1 FMI方法简介FMI方法是一种以3天的地磁场X和Y分量分均值观测数据为数据源,计算中间一天K指数的计算方法.FMI方法的基本思想是:首先设法求出X和Y两个地磁分量SR的时均值,再通过5次谐波拟合,得到SR曲线,最后从地磁分量时间序列中消去SR曲线,进而得到X和Y各自的K指数,并取其大者为最终的K指数[8].齐玮等[20]发现由于5次谐波拟合时的“外推”操作,FMI方法识别出的规则日变化SR在相邻两天的连接处存在较大的误差,因此建议在拟合中增加一个时均值数据来修正这一误差.下文SR时均值的获取,采用的是这种修正后的FMI方法,简便起见,仍称其为FMI方法.
2.2 径向基神经网络简介径向基神经网络是以函数逼近理论为基础而构造的一类前向型神经网络,这类网络的学习等价于在多维空间中寻找训练数据的最佳拟合平面.径向基神经网络的每个隐层神经元传递函数都构成了拟合平面的一个基函数,网络也由此而得名.径向基神经元的转移函数如公式(1),函数的图像如图 1所示.

|
图 1 径向基函数 Fig. 1 Radial basis function |
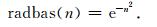
|
(1) |
径向基神经网络是一种局部逼近网络,即对于输入空间的某一个局部区域只存在少数的神经元用于决定网络的输出.而传统的BP(Back Propagation,反向传播)网络则是典型的全局逼近网络,即对每一个输入/输出数据对,网络的所有参数均要调整.由于二者的构造本质不同,径向基神经网络与BP网络相比规模通常较大,但学习速度较快,并且网络的函数逼近能力、模式识别与分类能力都优于后者,因此本文使用径向基神经网络对规则日变化进行建模.一个典型的径向基函数神经网络包括两层,即隐层和输出层.图 2是径向基神经网络的结构图,图中所示网络的输入维数为R、隐层神经元个数为S1、输出个数为S2,隐层神经元采用公式(1)所示的传递函数,输出层的传递函数为线性函数.图中ai1表示隐层输出矢量a1的第i个元素,iIW1,1表示第i个隐层神经元的权值矢量,即隐层神经元权值矩阵IW1,1的第i行.关于径向基神经网络的更多描述,可参考文献[21, 22].

|
图 2 径向基函数神经网络的典型结构 Fig. 2 Typical architecture of radial basis neural network |
磁扰和地磁纬度有着密切的关系,对于同一次扰动,磁纬越高,磁扰越强,但各台站所确定的K值又应当基本一致,因此不同磁纬的地区,K指数和磁扰的3小时变幅R的对应关系是不同的.本文的实验数据为北京地磁台(地理坐标:40.0°N,116.2°E;地磁坐标:29.63°N,191.84°E)1994~1997年共4年的分均值观测数据,所以应采用北京地磁台的K指数3小时扰幅[5].
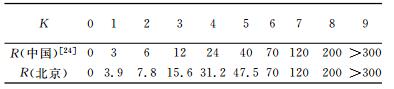
孙海军等认为:我国磁纬40°以下的地区,使用表 1所示的中国K指数3小时扰幅是合理的,并且与北京地磁台基本处于同一磁纬的喀什地磁台(地理纬度39.5°,地磁纬度30.48°)也使用这一套K指数3小时扰幅[23].然而,表 1给出的中国K指数3小时扰幅是朱岗崑先生根据佘山台地磁观测数据制定的[24]-佘山台位于磁纬20.88°,而北京台位于磁纬29.63°,相差近9个磁纬度.为此齐玮等1)按照Bartels教授给出的K指数3小时扰幅确定原则,用频次比对的方法,以6年的分均值观测数据为基础,根据佘山地磁台的K指数和Kp指数,给出了北京地磁台的K指数3小时扰幅(表 1).本文使用的K指数3小时扰幅就是表 1所示的北京台3小时扰幅.
|
|
表 1 K指数与3小时扰动幅度最小值的对应关系 Table 1 K-indices and corresponding 3-hour disturbance range |
FMI方法分别标定X、Y两个分量的K指数,取其大者为最终的K指数.也就是说,为了实时标定K指数,必须对X和Y两个分量的SR时均值分别建模.但是国内地磁台站标定K指数时,选取的并不是X和Y两个地磁分量,而是用H分量[1, 23],杨马陵等[25]提出将FMI方法直接用于H分量,称之为FMI-H(下文我们将修正后的FMI方法用于H分量,仍简称为FMI-H).假如用H分量标定K指数与用X、Y两分量标定的K指数非常近似,则只需对H一个地磁分量的SR时均值进行建模,从而简化了问题.
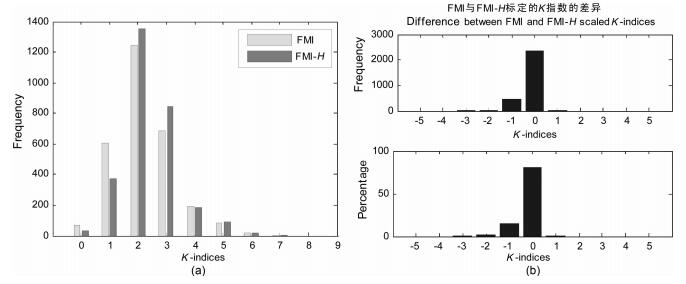
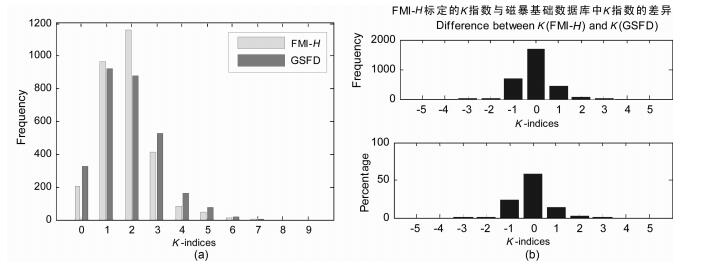
我们采用FMI方法和FMI-H方法分别标定了北京地磁台1997年1月1日至1997年12月30日共2912个K指数,并将标定的结果进行频次分布比较和同一3小时段标定差异比较,得到图 3a和3b.图 3表明:FMI-H与FMI标定的K指数频次分布非常接近,且在同一3小时段标定的K指数,完全吻合的占81.4%,相差一个标度的占17%,所以对北京地磁台来说,用H分量标定的K指数与用X、Y两分量标定的K指数没有什么太大的差别.再将FMI-H标定的K指数与磁暴基础数据库(GSFD:Geomagnetic Storm Fundamental Database,网址http://www.geomag.ac.cn)中北京台的K指数比较,得到图 4.图 4a为频次分布比较,图 4b为同一3小时段K指数差异比较.图 4表明:FMI-H标定的K指数与磁暴基础数据库中北京台的K指数频次分布也非常接近,且在同一3小时段,完全吻合的占57.6%,相差一个标度的占38.71%.事实上,从与磁暴基础数据库中北京台K指数的吻合度来看FMI-H略优于FMI-后者与基础数据库中北京台K指数完全吻合的占54.2%,相差一个标度的占39.7%1).以上两个实验表明:对于北京地磁台,用H分量来标定K指数是合理的,因此我们选择H分量的SR时均值进行建模.
|
图 3 FMI与FMI-H标定K指数比较(1997年1月1日至12月30日共2912个K指数) Fig. 3 Comparison between K-indices scaled by FMI and FMI-H (2912 K-indices from Jan 1, 1997 to Dec 30, 1997) |
|
图 4 FMI-H标定K指数与磁暴基础数据库中北京台K指数比较(1997年1月1日至12月30日共2912个K指数) Fig. 4 Comparison between FMI scaled K-indices and K-indices from GSFD (2912 K-indices from Jan 1, 1997 to Dec 30, 1997) |
1) 齐玮,王秀芳,李夕海等.北京地磁台K指数3小时扰幅修正及K指数自动标定.已投地球物理学报
4 基于径向基神经网络的规则变化建模与预测 4.1 规则变化SR的建模 4.1.1 模型的输入与输出
设t表示日期,第t日H分量规则日变化SR的时均值记作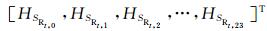
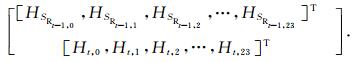
|
以当天的H分量规则日变化SR的时均值为神经网络的输出,因此输出向量可以表示成

|
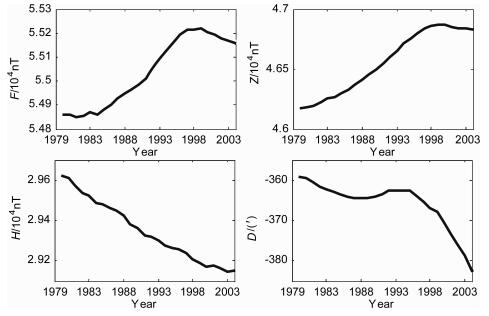
因为我们用到的数据长达4年(1994~1997年),所以在训练神经网络之前必须消除地球主磁场的长期变化,否则会造成神经网络输入空间的漂移,从而导致网络规模的非理性扩张(隐层增加了不必要的神经元)及预测精度的降低.易世华、齐玮等[26]研究了北京地磁台1979~2004年地磁场的长期变化特征,图 5为该台站F、Z、H、D四个分量的长期变化曲线.由图 5可见:1979~2004年,北京地磁台的地磁场H分量,总体上呈线性下降趋势,1979年为29625.09 nT,而2004年仅为29150.21 nT,26年中共下降了474.88 nT,平均年变率约为-19 nT/a.因此,我们以-19 nT/a的年变率来消除地球主磁场的长期变化.
|
图 5 北京地磁台1979~2004年F、Z、H、D四分量的长期变化曲线 Fig. 5 Geomagnetic secure variation form 1979 to 2004 at Beijing Observatory |
径向基神经网络有两个参数:扩展常数spread和拟合误差.扩展常数spread控制径向基神经元的响应在模型输入空间的交叠程度,一般应使spread足够大,以保证径向基神经元的响应在输入空间能够交叠,但spread也不能过大,否则径向基神经元的响应在输入空间过分交叠,弱化了神经元的个体差异,导致所有的神经元都有相似的表现.拟合误差参数指的是:训练误差的平方和,其计算方法如公式(2),量纲为nT2.拟合误差取得越小,训练的精度越高、需要的神经元也越多,而模型也越复杂,但是过小的拟合误差会导致“过拟合”,从而降低了模型的泛化能力.
我们分两步来确定这两个参数:首先通过1994~1995年的数据来确定扩展常数spread,再用1996年的数据,在已知的spread下考察不同拟合误差的泛化能力,选定泛化能力最好的拟合误差参数.
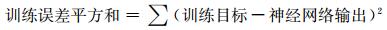
|
(2) |
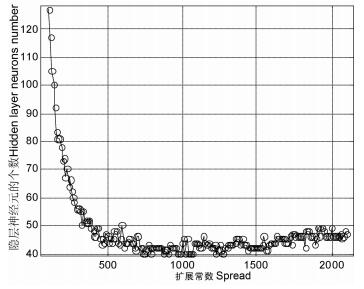
第1步,用1994~1995年的数据确定扩展常数spread.在固定的拟合误差下,扩展常数spread的不合理,表现为隐层产生了过多的神经元,使得模型过于复杂.因此,我们固定一个拟合误差,考察不同的扩展常数所对应的隐层神经元个数,选取隐层神经元个数最小时对应的扩展常数spread.这就存在一个问题:将拟合误差固定在什么数值才合理?事实上,如果拟合误差设定得太小,无论如何改变扩展常数spread,都会产生太多的神经元,因此拟合误差须设定得充分大,这样使得计算复杂度也比较低.当然,拟合误差也不能设定得过大,否则神经网络得不到充分的训练,无论如何改变扩展常数spread,隐层也只有几个神经元.经过几次调整,最终将拟合误差参数固定在100000 nT2.下文可以看到,这样一个值与最终确定的拟合误差值相比,差别是非常大的,因此确定扩展常数时拟合误差参数的选取是比较自由的.由实验可知:当扩展常数为740时,需要的隐层神经元最少-仅有40个.图 6给出了拟合误差固定在100000 nT2时,不同扩展常数对应的隐层神经元个数.
|
图 6 径向基神经网络扩展常数的选取 Fig. 6 Choose the spread of radial basis function neural network |
第2步,在已知的扩展常数下,选择拟合误差参数.具体方法是:将扩展常数设为第1步选定的740,在不同的拟合误差下,以1994~1995年的数据训练神经网络,再用1996年的数据检验此神经网络的泛化能力,选择泛化能力最好的拟合误差参数.我们用神经网络输出与检验数据(1996年的规则日变化时均值)的均方误差(Mean Square Error,MSE)来衡量模型的泛化能力,这里均方误差的计算方法如公式(3).

|
(3) |
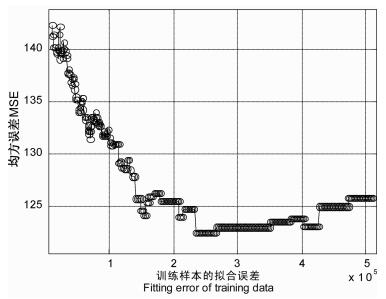
图 7给出了不同拟合误差下,神经网络模型的泛化能力.由图 7可见:当拟合误差参数在234000~265000 nT2之间时,径向基神经网络的泛化能力最好,我们取两者的均值249500 nT2.可见,这里确定的拟合误差,是第1步确定扩展常数时选取的拟合误差(100000 nT2)的2倍多,因此我们说第1步确定spread时设定的拟合误差是比较自由的.此外,由于下面我们将用1994~1996年3年的数据训练神经网络,而这里的拟合误差定义为“误差平方和”,所以当训练数据增加50%时(多了1年),拟合误差也应增大50%,即374250 nT2.
|
图 7 径向基函数神经网络拟合误差的选取 Fig. 7 Choose the fitting error parameter of radial basis neural network |
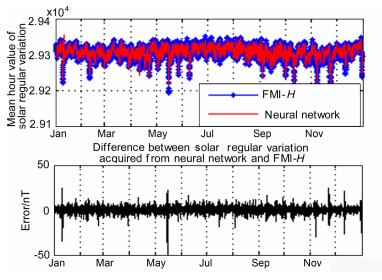
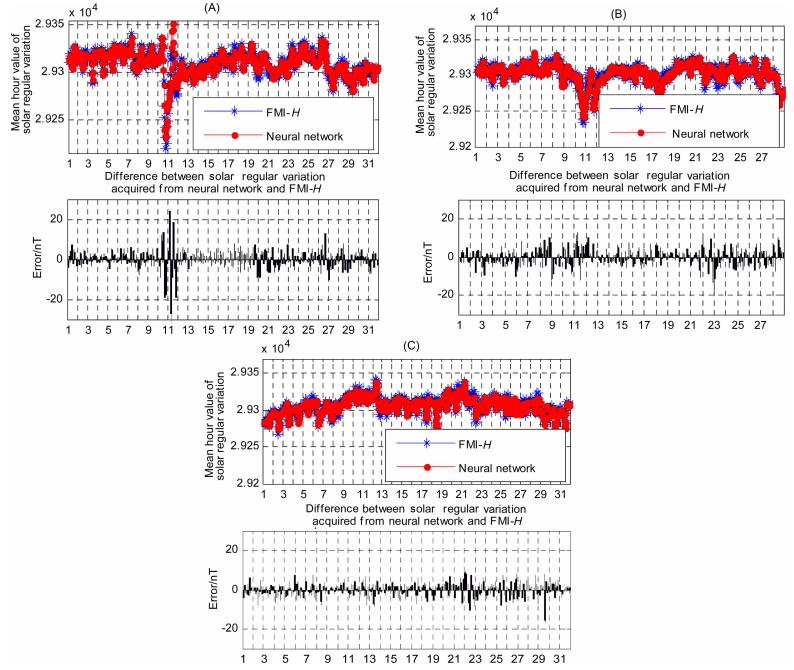
我们将扩展常数设为740、拟合误差设为374250 nT2,用1994~1996年3年的数据进行神经网络训练,得到了一个隐层包含17个神经元的径向基神经网络.用该神经网络模型获取1997年1月1日至12月31日的SR,结果如图 8所示,图中的误差指“FMI-H得到的1997年规则日变化与神经网络实时获取的规则日变化之差”.由图 8可见,规则日变化SR的实时获取是比较准确的,但是仍然有个别误差较大,为了探究误差的原因,我们将图 8的前3个月放大,得到图 9(A,B,C).
|
图 8 基于径向基神经网络的北京地磁台H分量规则日变化实时获取(1997年1月1日至12月31日) Fig. 8 Identify real-time solar regular variation by radial basis neural network (from Jan 1, 1997 to Dec 31, 1997) |
|
图 9 基于径向基神经网络的北京地磁台H分量规则日变化实时获取 (A)1997年1月;(B)1997年2月;(C) 1997年3月. Fig. 9 Identify real-time solar regular variation by radial basis neural network (A) Jan 1997; (B) Feb 1997; (C) Mar 1997. |
图 9A给出了1997年1月1日至31日神经网络实时获取的规则日变化,可见误差较大的地方出现在1月10日和11日,而这段时间正好发生了一次Dst指数峰值达到-78 nT,K指数达到6的中等磁暴.虽然只是一次中等磁暴,但此次磁暴却位列近年来的十大空间灾害性天气事件.事实上,规则日变化实时获取误差较大的时候,往往伴随着较大的不规则扰动,而图 8中最大的误差出现在1997年5月15日的一次Dst指数峰值达到-115 nT,K指数达到7的磁暴,此时误差达到了48.9 nT.Chen等[27]统计了Sq的逐日变化并发现:在某些强扰动时段,Sq变化的幅度有明显的增强,这暗示着“电离层导电性和(或)潮汐风速度的增大”;而在有些强扰动的时段Sq变化的幅度有显著的降低,这时“扰动发电机”过程起主导作用.因此,扰动较大时,规则日变化的实时获取难度非常大,这也是误差的主要来源.
图 9B给出了1997年2月1日至28日神经网络实时获取的规则日变化,这段时间只有2月27日发生了一次Dst指数峰值达到-86 nT,K指数达到5的中等磁暴,这个月规则日变化的实时获取是比较准确的.可见,对于K指数等于5的磁暴,我们训练的径向基神经网络依然有较高的性能;而图 9C是1997年3月1日至31日神经网络实时获取的规则日变化,这段时间没有发生磁暴,这个月的误差更小.这里根据公式(4)计算出1997年规则日变化实时获取的均方误差为14.8978 nT2,即3.8598 nT的标准误差.
5 K指数的实时标定5次谐波拟合径向基神经网络实时获取的规则日变化,再根据当天的分均值观测数据计算出纯扰动变化(K变化),根据表 1的北京台K指数3小时扰幅就可以得到实时标定的K指数.我们先比较实时标定的K指数与磁暴基础数据库中北京地磁台K指数的差异,再比较前者与FMI-H算法延迟一天标定的K指数之间的差异-对世界时1997年1月1日至1997年12月30日的2912个K指数,进行分布频次比较和同一3小时段标定差异比较. 图 10是径向基神经网络实时标定的K指数与磁暴基础数据库中北京台K指数的比较结果,图 11是实时标定(神经网络)与非实时标定(FMI-H)的比较结果.
|
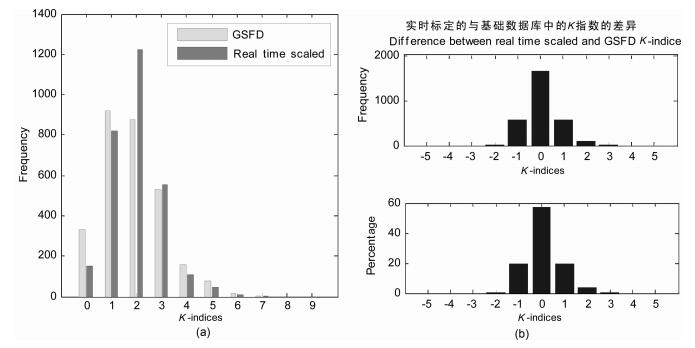
图 10 神经网络实时标定的K指数与磁暴基础数据库中K指数比较(1997年1月1日至12月30日共2912个K指数) Fig. 10 Comparison between real time scaled K-indices and K-indices from GSFD (2912 K-indices fromjan 1, 1997 to Dec 30, 1997) |
|
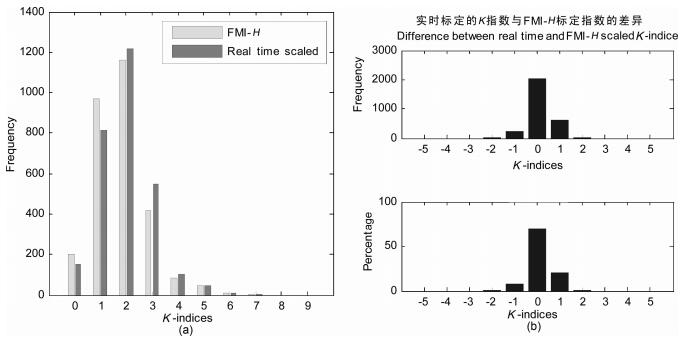
图 11 神经网络实时标定的K指数与FMI-H标定的K指数比较(997年1月1日至12月30日共2912个K指数) Fig. 11 Comparison between real time scaled and FM-H scaled K-indices (2912 K-indices from Jan 1, 1997 to Dec 30, 1997) |
由图 10a可见:当地磁场较平静时,与磁暴基础数据库相比,K指数实时标定的误差较大,而当地磁场扰动剧烈时,K指数的实时标定比较准确.这是因为K指数小于2时,3小时扰幅比较接近,很难确定K指数到底是0、1还是2,稍有误差就会导致K指数标定的不一致,但是对于地磁场微扰的基本判断(K≤2)是非常准确的.图 10b说明:在同一3小时段实时标定的K指数与磁暴基础数据库中的K指数完全吻合的占56.8%,相差一个标度的占39.2%,只有4%差别大于1个标度.回顾图 4:用FMI-H延迟一天标定的K指数,与磁暴基础数据库相比,完全吻合的占57.6%,相差一个标度的占38.71%.这说明与磁暴基础数据库中的K指数相比,神经网络实时标定K指数的准确率与用FMI-H延迟一天标定K指数的准确率非常接近.
图 11a显示:实时标定的K指数与FMI-H方法标定的K指数相比,其分布频次非常接近;而图 11b则进一步给出同一3小时段两者的差异:完全吻合的占69.8%,相差一个标度的占29.43%,差别大于1个标度的小于1%.无论是与磁暴基础数据库中的北京台K指数相比较,还是与FMI-H方法标定的K指数相比较,径向基神经网络实时标定的K指数都是比较准确的.
6 结语本文提出了一种基于径向基神经网络的K指数实时标定方法,以北京地磁台为例,用1994~1996年的数据训练了一个实时获取规则日变化的神经网络.用1997年的数据对该网络进行检验,实验结果表明:该方法能以3.8598 nT的标准误差实时识别规则日变化SR,且实时标定的K指数与直接用FMI-H方法延迟一天标定的K指数相比,完全吻合的占69.8%,差别大于一个标度的占0.77%.
| [1] | 徐文耀. 地磁学. 北京: 地震出版社, 2003 . Xu W Y. Geomagnetism (in Chinese). Beijing: Seismological Press, 2003 . |
| [2] | Matsushita S, Maeda H. On the geomagnetic solar quiet daily variation field during the IGY. J. Geophys. Res. , 1965, 70(11): 2535-2558. DOI:10.1029/JZ070i011p02535 |
| [3] | Wallace H Campbell. An introduction to quiet daily geomagnetic fields. Pure and Applied Geophysics (PAGEOPH) , 1989, 31(3): 315-331. |
| [4] | Chulliat A, Blanter E, Le Mouël J-L, et al. On the seasonal asymmetry of the diurnal and semidiurnal geomagnetic variations. Journal of Geophysical Research , 2005, 110: A05301. |
| [5] | Bartel J, Heck N H, Johnston H F. The three-hour range index measuring geomagnetic activity. Geophys. Res. , 1939, 44(4): 411-454. DOI:10.1029/TE044i004p00411 |
| [6] | Mayaud P N.Atlas of K-indices.Parti.IAGA Bull., 1967, (21), IUGG Publ.Office, Paris |
| [7] | Wilson L R. An evaluation of digitally derived K-indices. J. Goman. Golcr , 1987, 39: 97-109. |
| [8] | Sucksdorff C, Pirjola R, Häkkinen L. Computer production of K-values based on linear elimination. Geophysical Transactions , 1991, 36: 333-345. |
| [9] | Nowozynski K, Ernst T, Jankowski J. Adaptive smoothing method for computer derivation of K-indices. Geophys. J. Int. , 1991, 104: 85-93. DOI:10.1111/gji.1991.104.issue-1 |
| [10] | Clark T D G. Automatic K indices from the UK Geomagnetic Observatories British Geological Survey Technical Report WM/90/23. Edinburgh , 1990. |
| [11] | Clark T D G. Computer generated K indices adopted by the British Geological Survey. J. Atmos. Terr. Phys. , 1992, 54: 447-456. DOI:10.1016/0021-9169(92)90023-E |
| [12] | McNoe P A.Use of inclination in the automated derivation of geomagnetic K-indices.Oral Presentation at the 6th IAGA Scientific Assembly, Exeter, UK, 1989 |
| [13] | Walker J K. Adaptive separation of regular and irregular magnetic activity for K indices. J. Atmos. Terr. Phys. , 1987, 49: 1017-1025. DOI:10.1016/0021-9169(87)90108-5 |
| [14] | Wendt J. Numerical methods for K-scaling from digital data, applied to records from Wingst Observatory. J. Geophys. , 1988, 62: 175-179. |
| [15] | Hattingh M, Loubser L, Nagtegaal D. Computer K-index estimation by a new linear-phase, robust, non-linear smoothing method. Geophys. J. Int. , 1989, 99: 533-547. DOI:10.1111/gji.1989.99.issue-3 |
| [16] | Kadokura S. A new method to determine K-indices by using geomagnetic one-minute data. Memoriss of Kakioka Magenetic Observatory , 1988, 22: 45-61. |
| [17] | Golovkov V P, Papitashvili V O, Papitashvili N E. Calculations of K-index using the method of Natural Orthogonal Components. Geophys. Aeron. , 1989, 29: 514-517. |
| [18] | Menvielle M, Papitashvili N, Hakkinen L, et al. Computer production of K indices:review and comparison of methods. Geophys. J. Int. , 1995, 123: 866-886. DOI:10.1111/gji.1995.123.issue-3 |
| [19] | Bitterly M, Menvielle M, Bitterly J, et al.A comparison between computer derived (FMI method) and hand scaled K indices at Port Aux Francais and Port Alfred French Observatories.Rasson J Editeur.Proceedings of the Ⅵth International Workshop on Geomagnetic Instruments, Data Acquisition and Processing.Académie Royale de Belgique, Bruxelles, 1997.91~99 |
| [20] | 齐玮, 李夕海, 刘代志. FMI算法的疏漏及其修正.国家安全地球物理丛书(四):地球物理环境探测和目标信息获取与处理. 西安: 西安地图出版社, 2008 : 31 -35. Qi W, LiX H, Liu D Z. FMI algorithm's mistake and it's modification.National Secure Geophysics Series (4th):Earth Physical Environment Detecting and the Acquirement and Processing of Object Information (in Chinese). Xi'an: Xi'an Cartographical Publishing House, 2008 : 31 -35. |
| [21] | 许东, 吴铮. 基于MATLAB6.X的系统分析与设计-神经网络. 西安: 西安电子科技大学出版社, 2002 . Xu D, Wu Z. System Analysis and Design Based on MATLAB 6.X:Neural Network (in Chinese). Xi'an: Xidian University Press, 2002 . |
| [22] | 飞思科技产品研发中心编著. MATLAB6.5辅助神经网络分析与设计. 北京: 电子工业出版社, 2003 . Fectt Technology Production R & D Center. MATLAB 6.5 Assistant Neural Network Analysis and Design (in Chinese). Beijing: Publishing House of Electronics Industry, 2003 . |
| [23] | 孙海军, 高守全. 喀什地磁台数字与模拟记录K指数对比分析. 内陆地震 , 2007, 21(4): 348–353. Sun H J, Gao S Q. Record and simulation record for KASHI geomagnetic station. Intand Earthquake (in Chinese) , 2007, 21(4): 348-353. |
| [24] | 朱岗崑. 关于佘山地磁场扰动变化的分析. 地球物理学报 , 2001, 44(Suppl): 51–67. Tschu Kang-kun. Studies on the disturbance variations of geomagnetic field at So-Sè, near Shanghai, China. Chinese J.Geophys. (in Chinese) , 2001, 44(Suppl): 51-67. |
| [25] | 杨马陵, 刘昌谋, 叶东华, 等. FMI方法计算地磁K指数的初步研究. 地震地磁观测与研究 , 2004, 25(2): 55–61. Yang M L, Liu C M, YeD H, et al. Preliminary study of computing K indices with FMI method. Seismological and Geomagnetic Observation and Research (in Chinese) , 2004, 25(2): 55-61. |
| [26] | 易世华, 齐玮, 李志刚, 等. 北京地磁台地磁场变化特征初探.国家安全地球物理丛书(三):地球物理探测与应用. 西安: 西安地图出版社, 2007 : 124 -126. Yi S H, Qi W, Li Z G, et al. Primary research on variations of geomagnetic field at Beijing.National Secure Geophysics Series (3th):Earth Physical Detecting and Application (in Chinese). Xi'an: Xi'an Cartographical Publishing House, 2007 : 124 -126. |
| [27] | Chen G X, Xu W Y, Du A M, et al. Statistical characteristics of the day-to-day variability in the geomagnetic Sq field. J. Geophys. Res. , 2007, 112: A06320. |
 2010, Vol. 53
2010, Vol. 53