2. 地球空间环境与大地测量教育部重点实验室, 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
传统的海水质量变化确定主要依赖有限的海底压力测量数据,或海洋学模型[1],不能反映真实的总体海水质量变化,且实测的海底压力数据受环境限制而分布极其有限.随着卫星测高技术的发展,海平面的总体变化量得到了较为精确地确定,其变化量是比容和海水质量变化产生的海平面变化的叠加,而比容海平面的变化可以由实测的海水温度和盐度数据计算得到,从卫星测高数据所得海平面变化中扣除此变化量即得到海水质量变化,但其精度同样受到了实测海水温盐数据误差和分布不均匀的影响,此外,还将包含测高数据误差.
2002年发射的GRACE重力卫星,旨在获取高精度地球重力场的中长波分量及其时变特征.自GRACE计划实施以来,利用其提供的时变重力场数据反演全球和局部质量变化(主要是水文变化)进行了广泛的研究.Wahr等[2]首次提出由GRACE卫星的时变重力场数据可以反演地球表面物质质量分布的变化,包括陆地水存储、海水质量和大气质量等,并利用水文学、海洋学和大气模型进行了验证,给出了时变重力场球谐系数反演质量变化的数学模型.Chambers[3~5]对GRACE时变重力场反演海洋质量变化作了详细的研究,包括一阶项和C20项球谐系数对反演结果的影响、数据处理中相关项的改正等,其数值结果验证了由GRACE数据反演海洋质量变化的可行性和可靠性.殷述广[6]、周旭华[7]等利用较早期的GRACE时变重力场数据反演了海水质量变化,但其采用数据精度较差且没有考虑一阶项和C20影响,在研究区域性变化时,也未对信号泄漏进行处理.
本文基于最新的GRACE时变重力场进行了更精细详尽的数据处理,研究了适合的相关误差改正方法,反演得到了全球平均海水质量变化,在相同的时间和空间分辨率上与联合卫星测高和实测海洋温盐数据计算海水质量变化进行了比较,并对时空变化特性进行了详细的分析.计算结果与国际同类研究具有一致的年际变化和长期性趋势,显示了2003~2007年间全球温度升高,并导致冰川融化加速.
2 数学模型 2.1 GRACE反演海水质量变化地球是一个不断变化的动力系统,当某一区域内的物质重新分布时,引起密度分布的变化,则该区域内大地水准面产生变化.地球表面的质量迁移现象在年际时间尺度上主要集中在地球表面厚度为10~15 km的薄层内,其密度分布变化反映了包括大气、海洋、冰川以及陆地水储量等的变化.假设薄层的厚度足够小,由大地水准面球谐系数变化与密度变化的关系,顾及固体地球的滞弹性负荷形变,得到用大地水准面球谐系数变化表示的单位面积内海水质量变化[2]:

|
(1) |
其中,a为地球平均半径,θ和λ分别为余纬和经度,ρave是地球平均密度,约为5517 kg/m3,kn为负荷勒夫数,ΔCnm,ΔSnm为无量纲的球谐系数变化,可由GRACE时变重力场模型计算得到,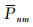
根据误差传播定律,由式(1),可得全球范围内海水质量变化误差的方差为
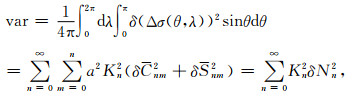
|
(2) |
其中,δ(Δσ(θ,λ))为海水质量变化误差,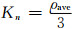
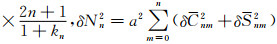
GRACE观测数据解算的大地水准面高位系数阶方差误差随阶数的增加迅速增大,由式(2),海水质量变化计算误差将随阶数增加也迅速增大,而高阶项球谐系数具有重要的贡献,因此,其误差对反演结果产生重大影响,将降低单点表面质量变化估计精度.在计算中,需引入空间平均函数以减弱高阶项球谐系数误差.
引入高斯滤波函数[2],海水质量变化反演公式为
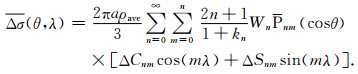
|
(3) |
在利用高斯滤波函数计算海水质量变化中,由于滤波平均半径较大,当处于海洋边界时,计算区域不仅包含了海洋信号,而且含有陆地信号,导致陆地水文和大气信号向海洋泄漏污染海洋上计算区域密度变化的GRACE重力场信号,造成海洋边界反演海水质量变化结果失真,同样,在陆地水储量变化反演中也会出现这样的问题.信号泄漏的影响可通过迭代的方法进行改正[2].首先,根据GRACE时变重力场信号反演出陆地表面质量变化,计算时,考虑海洋信号向陆地的泄漏,需选择尽量小的平均半径,同时需保证所选取半径对陆地表面质量变化反演的真实性,尽量消除GRACE时变重力场高阶项误差的影响.陆地表面质量变化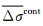
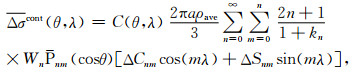
|
(4) |
其中,C(θ,λ)为“流域函数”,当计算点位于陆地时,C(θ,λ)=1;位于海洋时,C(θ,λ)=0.
将式(4)得到的陆地表面质量变化作球谐级数展开,反解得到对应的球谐系数变化,然后由式(3)计算海洋范围内的质量变化,这部分海水的质量变化可认为是陆地表面质量变化在海洋上的信号泄漏.当然,也可以从GRACE的球谐系数变化中扣除陆地表面质量变化产生的球谐系数变化后,作为对海水质量变化产生的球谐系数变化,再利用式(3)计算海水质量变化.本文直接计算了陆地表面质量变化在海洋上的信号泄漏进行改正.
2.3 比容海平面变化比容海平面变化可由海洋现场观测温度和盐度数据计算[4, 8]:
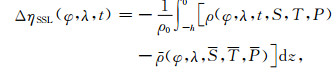
|
(5) |
其中,ρ0为海水平均密度,φ和λ分别为计算点纬度和经度,t为观测历元,海水密度ρ是盐度S、温度T和压强P的函数[9],P可由海水深度得到.平均海水密度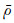
本文选取美国德克萨斯大学空间研究中心(UTCSR)发布的2003年1月至2006年12月间Release-04版本GRACE月时变重力场模型,其球谐系数完整到60阶次.所选时间段内缺少2003年6月数据,总共时间跨度为47个月.首先,将所选时间内的月重力场球谐系数减去时间内的平均值获得每月重力场球谐系数的变化量;其次,重力场模型系数C20反映了地球形状的扁度(扁率)产生的重力位扰动(异常),GRACE卫星由于近圆轨道设计而对重力场C20项不敏感,导致该项解算精度不高,此外,在GRACE时变重力场模型解算中,将GRACE地球坐标系原点与地球瞬时质量中心重合,使得无法估计反映出包含海洋、陆地和大气质量交换所体现的一阶项变化,而实际上我们说的海洋或陆地的质量变化是相对于一个固定的地球质量中心(如国际地球坐标系ITRF原点)对应的地球质量空间分布,理论上,在计算中应考虑这一影响,因此,本文替换了C20项球谐系数,并增加了一阶项球谐系数变化,其中,C20项球谐系数选取卫星激光测距计算结果[10],该结果同样由UTCSR给出,计算中采用了与GRACE时变重力场相同的背景场,一阶项变化选取由海洋学模型和陆地GRACE数据估计的每月地心坐标参数[11];最后,考虑与卫星测高数据比较的一致性,恢复了大气质量与正压海洋信号的时变效应,并在卫星测高数据处理中作了逆气压改正,在500km半径的高斯滤波和球谐系数相关性误差滤波后得到全球海水质量变化时间序列.相关性误差滤波基于球谐系数系统相关误差的思想[12],作适当的改进,保留一阶次以下球谐系数不变,但对阶数大于11的2次以上相同奇数或偶数次系数,分别利用一个7阶多项式进行拟合,然后获取拟合后的残差作为球谐系数的变化,再由式(3)计算海水质量变化.
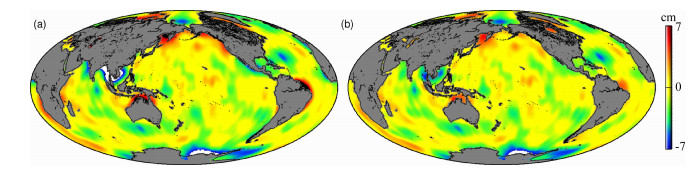
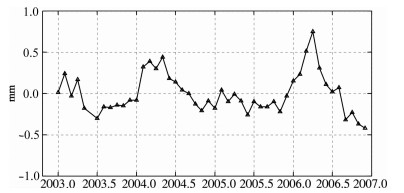
上述方法计算的海水质量变化受高斯滤波影响,在海洋边界处,陆地水文信号向海洋泄漏,造成海水质量变化偏大,如图 1中,特别是南美亚马逊流域、北极圈附近、澳大利亚北部、亚洲恒河流域及非洲赞比西河流域等信号泄漏较大.本文首先利用GRACE月重力场球谐系数变化,选取250 km的高斯平滑半径计算全球陆地水储量变化,将此变化作球谐级数展开,获得相应的球谐系数变化.然后,利用此变化量作为计算全球海水质量变化的陆地水文信号泄漏,在原始月重力场球谐系数变化计算的全球海水质量变化中扣除,得到信号泄漏改正之后的海水质量变化[2],信号泄漏对全球平均海水质量变化影响为10%左右(图 2).
|
图 1 2006年5月信号泄漏改正前(a)和改正后(b)全球海水质量变化 Fig. 1 Global ocean mass variations with leakage corrected before (a) and after (b) in May, 2006 |
|
图 2 信号泄漏改正前后月平均海水质量变化之差 Fig. 2 Differences between monthly global mean ocean mass variations with leakage corrected before and after |
利用2003年1月至2006年12月间Jason-1 GDR-B数据,经过对流层干、湿分量改正,电离层改正,海洋潮汐改正,固体潮改正,海况偏差改正以及逆气压改正等预处理,由10天观测周期数据基于共线平差方法获取每个月的沿轨全球平均海平面高.以所选时间内所有周期的共线平均作为海平面变化计算的参考值,计算得到每月的沿轨全球平均海平面变化.由于GRACE数据处理中,对其球谐系数作了500 km的高斯平滑,为在相同的尺度上与其进行比较,对得到的沿轨平均海平面变化依次做了如下处理:1°×1°格网化、60阶次球谐系数展开、500 km半径高斯平滑、恢复为1°×1°格网海平面变化[3].
3.2.2 比容海平面变化选取了美国国家海洋数据中心海洋气候实验室提供的1°×1°格网WOA05海洋月平均温度[13]和盐度模型[14],及日本气象局Ishii[15]计算的海洋温度和盐度资料.Ishii海洋温度和盐度资料基于WOD05实测数据和WOA05模型,采用近实时的GTSPP(Global Temperature and Salinity Profile Project,全球温盐剖面计划)温盐剖面数据,添加日本海洋数据中心提供的上述两种数据中未使用的XBT(eXpendable Bathy Thermograph,“抛弃式”深海温度测量仪)数据,进行XBT和MBT(Mechanical Bathy Thermograph,机械式深海温度测量计)偏差校正后得到,其时间跨度为1945~2006年,时间分辨率为1个月,空间分辨率为1°×1°,沿海水深度0~700 m垂直分16层.
WOA05月平均模型垂直分层为24层,深度为0~1500 m,其年平均模型垂直分层为33层,深度为0~3300 m.本文为了与Ishii数据结果进行比较,计算比容海平面变化时,两种数据均只算到700 m.采用WOA05时,以其年平均模型作为平均值,采用Ishii数据时,以其4年的算术平均作为平均值.利用式(5)分别计算每月1°×1°格网比容海平面变化后,为保证相同尺度的比较,与测高数据进行了相同的处理.
基于全球测高海平面变化与海洋学比容海平面变化,同时考虑冰后回弹对海面高的影响,由测高海平面高变化等于海水质量变化等效水高与比容海平面变化之和,即可得到由于全球海水质量变化引起的等效水高.
4 结果与分析利用GRACE、卫星测高和海洋温盐数据按上述方法处理后,以权因子cosφ定权分别建立了GRACE卫星数据直接反演的海水质量变化和全球平均海平面变化、比容海平面变化的时间序列,并利用最小二乘法拟合得到了偏差、长期性趋势变化、周年和半周年变化.
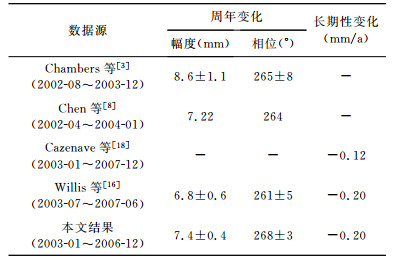
GRACE时变重力场反演的全球海水质量长期性变化为-0.2±0.2 mm/a,周年变化幅度为7.4±0.4 mm,相位为268°±3°.冰后回弹对海水质量变化有长期性影响,采用不同的冰后回弹改正模型,其对海水质量长期性趋势变化影响不同,约为1~2 mm/a,如,Willis等[16]采用1 mm/a;Lombard等[17]采用1.7 mm/a;而Cazenave等[18]采用2 mm/a. 表 1中给出了其他学者和本文所计算的相关时间段内全球海水质量变化,其中,Willis等的长期性变化为0.8±0.8 mm/a,扣除其采用的冰后回弹改正1 mm/a之后为-0.2 mm/a.从表 1可以看出,本文利用GRACE时变重力场反演的全球海水质量周年变化特征和长期趋势(未加冰后回弹改正结果)均与国际一致.
|
|
表 1 GRACE时变重力场反演的全球海水质量变化 Table 1 Global ocean mass variations from GRACE time-variable gravity data |
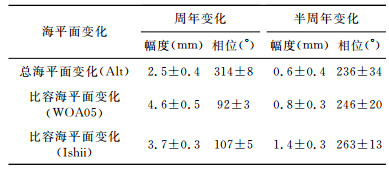
卫星测高数据计算的全球平均海平面长期性变化为2.1±0.2 mm/a,周年变化幅度为2.5±0.4 mm,相位为314°±8°,见表 2.海盆形状和容积受到冰后回弹的影响而在不断地发生改变,即海盆相对深度加深,使海平面具有0.3 mm/a的下降趋势[19],进行该项改正后的测高海平面长期性变化为2.4±0.2 mm/a,与Cazenave等[18]所给出的2.5±0.4 mm/a基本一致.
|
|
表 2 卫星测高和海洋温盐数据计算的全球海平面变化 Table 2 Global mean sea level variation from altimetry and ocean data |
本文利用Ishii数据得到的全球比容海平面长期性趋势变化为-0.5±0.2 mm/a,周年变化幅度为3.7±0.3 mm,相位为107°±5°.由于WOA05只包含了12个月的数据,其数值为多年观测数据的平均,不能反映长期性趋势,所反映的周年变化幅度为4.6±0.5 mm,相位为92°±3°.Willis等[16]利用2003年7月至2007年6月的Argo海洋浮标观测数据计算的比容海平面周年变化幅度为3.7±0.8 mm,相位为104°±13°,长期性趋势变化为-0.5±0.5 mm/a,均与本文结果符合较好;Cazenave等[18]利用比Willis等长约1年的Argo数据(2003-01~2007-12)计算的长期性趋势变化为0.37±0.1 mm/a,略高于Willis等的结果.这些数据说明了比容海平面上升速率在最近几年发生了显著变化.
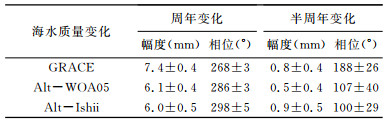
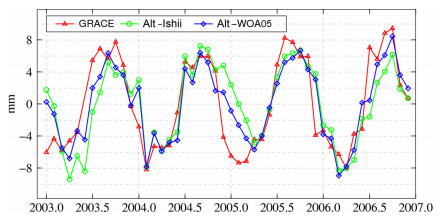
利用测高海平面变化和比容海平面变化时间序列,在对应月份相减后得到了海水质量变化的时间序列,再由最小二乘拟合得到周年变化特征和长期趋势变化,见表 3.可以看出,由GRACE时变重力场反演的全球海水质量周年变化与卫星测高联合海洋温度和盐度数据获得的海水质量变化非常相近(图 3),其中,由于模型数据WOA05是多年平均值,因此,其反映的海水质量变化周年特征更接近GRACE数据反演结果.而半周年变化特征受局部气候和现象(如厄尔尼诺等)影响较大并不保持严格重复.图 3给出了移去偏差和长期性趋势之后,卫星测高所得总体海平面变化减去比容海平面变化结果,及GRACE时变重力场反演海水质量变化结果.
|
|
表 3 GRACE、卫星测高和海洋温盐数据反演的全球海水质量变化 Table 3 Global ocean mass variations from altimetry, GRACE and ocean data |
|
图 3 GRACE时变重力场,及联合卫星测高和海洋温盐数据反演的全球海水质量变化时间序列 Fig. 3 Time series of global ocean mass variations from GRACE observations and combined altimeter and oceanic data |
由上述比较和分析可以得出,本文由GRACE时变重力场计算的结果可以认为是可靠的,由测高和海洋温盐数据计算结果与相关同类研究结果都符合较好,因此表 3中周年变化之差产生的原因可能是,卫星测高数据在处理中由于未考虑时间的严格统一,所得月平均数据只是若干周期的共线平均,而每个周期的时间跨度太大(10天),可能在某一个月的数据中引入了上一个月或下一个月的数据,不能真实反映该月的变化量.此外,卫星测高数据预处理中各项地球物理改正的误差,以及忽略年代际周期变化和700 m以下比容海平面的变化等对海水质量变化反演也有一定影响.
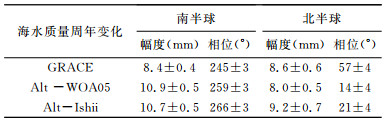
进一步对南、北半球的计算结果进行了统计和比较分析(表 4).受卫星测高数据预处理和时间不严格一致的误差,以及深海比容海平面变化和年代际变化特征影响,南半球的联合卫星测高和海洋温盐数据得到的海水质量变化与GRACE时变重力场反演的海水质量变化周年幅度差约1~3 mm,相位差约20°,北半球的周年幅度差约1~2 mm,相位差约40°.GRACE反演的南北半球海水质量周年变化幅度大致相同,但相位近乎相反.
|
|
表 4 由GRACE时变重力场、卫星测高和海洋温盐数据反演的南、北半球海水质量周年变化 Table 4 South and North hemisphere mean ocean mass annual variations from altimetry, GRACE and ocean data |
综合表 3和表 4可以看出,全球平均海水质量变化和南半球海水质量变化幅度较为接近.这说明,在计算全球平均海水质量变化中,南半球所占比例较重,其原因可能是南极大陆冰融量比格陵兰大,2003~2008年期间南极冰盖融化对全球海平面上升的贡献为0.56±0.06 mm/a,大于格陵兰岛贡献(0.38±0.05 mm/a)[18].
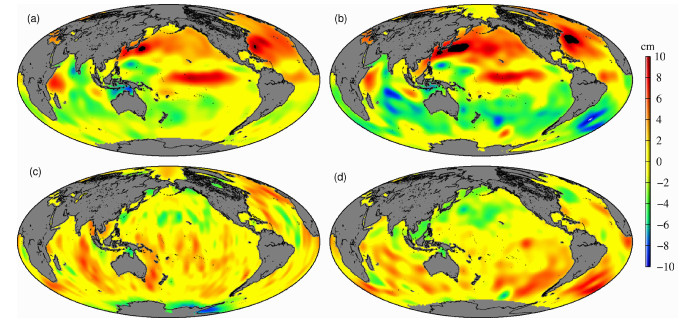
图 4给出了2004年9月分别由卫星测高数据,Ishii温度和盐度数据及GRACE时变重力场计算的全球海平面变化.由于南半球海洋范围宽广,实测温度和盐度数据有限,导致比容海平面变化误差较大,如南大西洋,由此使得联合卫星测高和温盐数据获取的海水质量变化在南大西洋和南太平洋东岸与GRACE反演结果有较大的差值.
|
图 4 2004年9月全球海平面变化 (a)测高海平面变化;(b)Ishii数据比容海平面变化;(c)GRACE数据海水质量变化;(d)扣除比容后卫星测高所得海水质量变化. Fig. 4 Spatial distribution of sea surface variations in Sep. 2004 (a)From altimeter observation; (b)Steric sea level change from Ishii data; (c)Ocean mass variation from GRACE observation; (d)Difference between(a) and (b). |
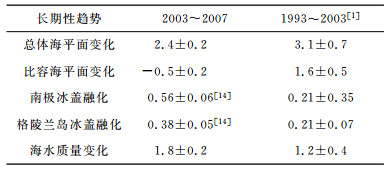
比较三种数据所得长期性趋势,经冰后回弹改正(取2 mm/a时)后GRACE反演海水质量变化占卫星测高数据计算总体海平面变化比例最高可达75%左右,而由海洋温度和盐度数据所得比容海平面变化呈现负值或很小的正值,相比于1993~2003年期间结果[1],海水质量变化所占比例增加,成为了海平面上升的主要影响因素,比容海平面变化所占比例下降(表 5).表明了全球温度升高,冰川融化加速,海水质量增加,而海水比容由于大量冰川融水影响而变化较小,因此,比容海平面只有微小变化.
|
|
表 5 2003~2007年期间与1993~2003年期间长期性趋势变化比较(单位:mm/a) Table 5 Comparison of long term trends between 2003~2007 and 1993~2003(unit:mm/a) |
利用GRACE时变重力场数据反演的全球海水质量周年和长期性趋势变化与国际同类研究结果比较符合较好;与联合卫星测高和海洋温盐数据获得的海水质量变化比较,结果相近,主要为卫星测高数据预处理误差和时间不严格一致影响,加之南半球温盐数据的缺乏以及忽略了深海比容海平面变化和年代际变化特性等.
由卫星测高、GRACE时变重力场和海洋温盐三种数据获取的长期性趋势变化,相比于IPCC第4次评估报告公布的1993~2003年间各变化量[1],可以认为:自2003年后,全球海平面变化总量呈上升趋势,但速率减缓,由3.1 mm/a降至2.4 mm/a;海水质量变化在海平面变化总量中所占比例增大,冰后回弹改正(取2 mm/a时)后全球海水质量长期性趋势变化最大可达1.8 mm/a,占测高总体海平面变化的75%;由Argo和Ishii实测数据计算的比容海平面变化,均表明比容变化引起全球海面高变化所占比例较小.从而表明了2003~2007年间全球温度升高,冰川融化加速,海水质量增加,而海水温度由于大量冰川融水影响而变化较小.
| [1] | Bindoff N, Willebrand J, Artale V, et al. Observations: oceanic climate change and sea level, in Climate Change 2007: The Physical Science Basis. Contribution of Working Group 1 to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, 2007. 385~432 |
| [2] | Wahr J, Molenaar M, Bryan F. Time variability of the Earth's gravity field: hydrological and oceanic effects and their possible detection using GRACE. J.Geophys. Res. , 1998, 103(B12): 30205-30230. DOI:10.1029/98JB02844 |
| [3] | Chambers D, Wahr J, Nerem R. Preliminary observations of global ocean mass variations with GRACE. Geophys. Res. Leu. , 2004, 31(13): L13310. |
| [4] | Chambers D. Observing seasonal steric sea level variations with GRACE and satellite altimetry. J.Geophys. Res. , 2006, 111(C3): C03010. |
| [5] | Chambers D. Evaluation of new GRACE time-variable gravity data over the ocean. Geophys. Res. Lett. , 2006, 33: 17. |
| [6] | 殷述广, 朱耀仲, 钟敏, 等. 全球海水质量季节变化研究. 大地测量与地球动力学 , 2005, 25(4): 33–37. Yin S G, Zhu Y Z, Zhong M, et al. Study on seasonal variations of global ocean mass. Journal of Geodesy and Geodynamics (in Chinese) , 2005, 25(4): 33-37. |
| [7] | 周旭华, 吴斌, 彭碧波, 等. 全球水储量变化的GRACE卫星检测. 地球物理学报 , 2006, 49(6): 1644–1650. Zhou X H, Wu B, Peng B B, et al. Detection of global water storage variation using GRACE. Chinese J. Geophys. (in Chinese) , 2006, 49(6): 1644-1650. |
| [8] | Chen J, Wilson C, Tapley B, et al. Seasonal global mean sea level change from satellite altimeter, GRACE, and geophysical models. Journal of Geodesy , 2005, 79(9): 532-539. DOI:10.1007/s00190-005-0005-9 |
| [9] | Fofonoff N, Millard R. Algorithms for computation of fundamental properties of seawater. Unesco Technical Papers in Marine Science , 1983. |
| [10] | Cheng M, Tapley B. Variations in the Earth's oblateness during the past 28 years. J. Geophys. Res. , 2004, 109(B9): B09402. |
| [11] | Swenson S, Chambers D, Wahr J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. , 2008, 113(B8): B08410. |
| [12] | Swenson S, Wahr J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. , 2006, 33: L08402. |
| [13] | Locarnini R, Mishonov A, Antonov J, et al. World Ocean Atlas 2005, vol. 1, Temperature. In: Levitus S ed. NOAA Atlas NESDIS, vol. 61. NOAA, Silver Spring, Md, 2006. 182 |
| [14] | Antonov J, Locarnini R, Boyer T, et al. World Ocean Atlas 2005, vol. 2, Salinity. In: Levitus S ed. NOAA Atlas NESDIS, vol. 62. NOAA, SilverSpring, Md, 2006. 182 |
| [15] | Ishii M, Kimoto M. Reevaluation of historical ocean heat content variations with time-varying XBT and MBT depth bias corrections. Journal of Oceanography , 2009, 65(3): 287-299. DOI:10.1007/s10872-009-0027-7 |
| [16] | Willis J, Chambers D, Nerem R. Assessing the globally averaged sea level budget on seasonal to interannual timescales. J. Geophys. Res. , 2008, 113: C06015. |
| [17] | Lombard A, Garcia D, Ramillien G, et al. Estimation of steric sea level variations from combined GRACE and Jason-1 data. Earth and Planetary Science Letters , 2007, 254(1-2): 194-202. DOI:10.1016/j.epsl.2006.11.035 |
| [18] | Cazenave A, Dominh K, Guinehut S, et al. Sea level budget over 2003-2008: a reevaluation from GRACE space gravimetry, satellite altimetry and Argo. Global and Planetary Change , 2009, 65(12): 83-88. |
| [19] | Douglas B, Peltier W. The puzzle of global sea-level rise. Physics Today , 2002, 55(3): 35-41. DOI:10.1063/1.1472392 |
 2010, Vol. 53
2010, Vol. 53