自1970年世界上第一台电离层加热装置Platteville在美国Boulder(40.18°N,104.73°W)建成至今,世界各地又相继建成了众多的电离层高频人工变态装置,包括美国的HIPAS(以及后来的HAARP),俄罗斯的SURA,欧洲EISCAT计划中的Tromsø等等.利用这些大功率加热机得到了很多有价值的实验结果,包括加热产生的一级时空效应[1, 2]和二级时空效应[3~5].
在高频电磁波加热电离层中,泵波反射高度处折射率接近于0,使其电场增幅明显增大[6],该因素引起的偏移吸收导致泵波反射高度附近区域成为除低电离层(D、E层)外的另一个主加热区[7].偏移吸收会引起该区域电离层内泵波反射高度处出现中大尺度的电子浓度和电子温度的变化.
关于加热中电子浓度、电子温度变化的理论以及数值模拟研究已有作者讨论过[8~10],其结果多为一维数值模拟,对于扩散系数和热传导系数都很小的D,E层是基本适用的,但在场向扩散系数比横向传导系数高数个量级的F层则存在明显的偏差,此时电离层被加热区域与泵波直接照射区域明显不同,加热导致的电离层空间形态也将有所不同,因此建立完整的高频加热电离层二维模型将更有助于对加热效应的深入理解和阐述.
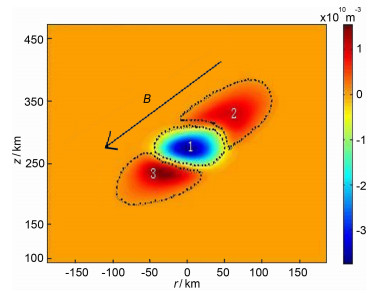
对高频泵波加热电离层理论模型及数值模型的详细介绍和一般情况下的二维模拟结果已经在文献[11]中给出.模拟加热结果表明,当高频泵波入射到电离层中时,沿着穿过泵波反射区域的磁力线方向将会出现三个区域明显的电子浓度变化,如图 1.其中泵波反射高度附近电子浓度迅速下降,图中标为1区域,而在逆着穿过此区域的磁力线方向(2区域)与沿着穿过此区域的磁力线方向上(区域3),则会分别出现电子浓度稠团.(为了方便下文的表述,后文模拟结果中同样可以将加热区域分为与图 1类似的三个区域).其中逆着磁力线方向上的稠团不甚明显,且会很快消失,较少被实验观测到,泵破反射区域的空洞与沿着穿过此区域的磁力线方向上的稠团则得到文献的证实[8, 12].加热中电子温度上升幅度随初始加热条件不同而介于2 5%~9 0%之间,最大电子浓度稠团和空洞的相对变化率分别为10%和-13%,其结果与文献[13]所获结果基本一致.此外,模拟结果中电离层电子温度、电子浓度的饱和与冷却时间尺度也与EISCAT雷达观测到的Tromsø加热实验结果基本相同[12].
|
图 1 文献[11]得到的夜间模拟加热 20s后电子浓度绝对变化量剖面箭头B表示磁场方向. Fig. 1 Modeling absolute change of ne after 20 s HF ionospheric heating at night |
尽管前文介绍的模拟结果能够基本反映众多泵波加热电离层实验结果,然而在对高频加热中泵波反射区域进行诊断观测中,时常能够观测到一些不同寻常的电子浓度、电子温度变化[14, 15],如Arecibo就曾在高频加热中观测到大尺度区域内+300%电子温度、-25%电子浓度变化[16],曾有作者利用自聚焦不稳定性理论来解释这种反常的加热结果[17].另外在一些高频泵波加热电离层实验中[18, 19],电子温度、电子浓度随时间的变化更加复杂,电子温度在加热机开关机一段时间后并没有达到稳定,以及电子浓度在加热中的不规则变化,本文介绍的不稳定机制或许可以解释以上实验结果.
前文在利用加热模型进行模拟加热中[11],虽然不同电离层电子浓度、电子温度的空间结构对模拟加热结果有一定影响,但是在大部分平静电离层背景下模拟结果基本上是一致的.然而当模拟加热的初始电子浓度、电子温度结构满足一定条件时,模拟加热电离层泵波反射区域出现一种正反馈机制,这一机制使得电子浓度、电子温度随加热机开关机的响应出现明显不同,且电子浓度、电子温度的变化也更加强烈.
本文首先利用文献[11]中的加热机制理论和数值模拟方法,以中纬度平静电离层为背景,进行地基高频电波加热的数值模拟.然后从电离层加热的物理机制的角度,结合具体模拟结果,逐项分析加热的物理模型,对地基高频电磁波加热的数值模拟结果正反馈机制进行分析,找出导致该特殊模拟加热结果的源项,并对模拟结果进行解释.
2 模拟结果本文使用的模拟加热模型如下[11]:动力学方程:
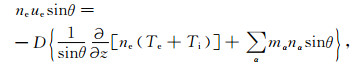
|
(1) |
连续性方程:
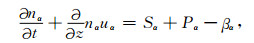
|
(2) |
电子能量守恒方程:
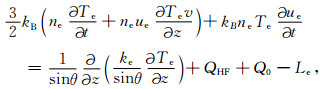
|
(3) |
上式中kB表示玻尔兹曼常数,D表示等离子体扩散系数,Te、Ti分别为电子温度和离子温度,mα、nα、uα(α可以为电子,NO+,O2+,O+)分别为电子或离子的粒子质量、浓度和扩散速度,Pα,βα分别为离子的产生率和消失率,ke表示热传导系数,QHF表示泵波能量源项,Le表示电子能量损失项,Sα,Q0是为使各参量稳定于初始状态而引入的额外源项.
尤其值得注意的上式QHF,其大小直接影响模拟加热结果.此时QHF不但包括欧姆加热,还包括波-波、波-粒相互作用引起的反常吸收.其具体计算方法如下:首先做以下假设,电离层对泵波能量吸收在高度和水平方向上都满足以反射点为中心的高斯分布,前者可以由泵波天线方向图大致证明,后者可由实验观测知其大致满足高斯分布[19].泵波反射点处源项QHFmax为
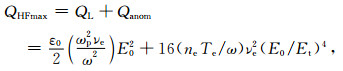
|
(4) |
其中QL为欧姆吸收,反常吸收Qanom利用饱和光谱方法[20]计算而来,电场强度E0利用经验公式E0=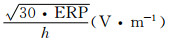
模拟加热地点仍为武汉(114.7°E,30.5°N),地磁纬度:18.8°,磁倾角:45°,加热时间2007年9月1日,加热有效辐射功率(ERP)100 MW,以上模拟加热条件与文献[11]完全相同,仅将加热时间选为LT16:00,高频泵波的频率为8.25 MHz,其时电离层临界频率为8.52 MHz,泵波反射高度同样在250 km附近.加热时间为300 s,并观察关机后600 s内Te和ne的变化.为了方便表述,规定位于加热机正上方泵波反射高度处的点称为加热中心(位于图 1中1区域).模拟加热背景电离层模型选自IRI-2007,其电子浓度、电子温度二维剖面见图 2,大气模型选取NRLMSISE-00.
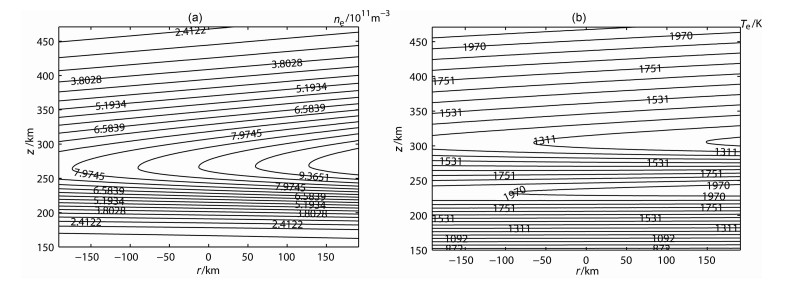
|
图 2 武汉地区2007年9月1日16:00初始参数的二维剖面等高图 (a)电子浓度(1011m-3)等高图;(b)电子温度(K)等高图. Fig. 2 Contour map of ne(a) and Te(b) before the ionospheric heating |
加热机开机不同时间后电子浓度电子温度的数值模拟结果如图 3所示.由图 3a,图 3b可知,+2 s后(+2 s表示加热开始时刻以后2s,后文与此相同,超过+300 s表示已经关机)电子温度上升幅度较小,加热中心处电子温度上升至2019 K,变化率为11.5%,比LT20:00[11]加热2 s后电子温度42%的上升小的多,此时电子浓度没有明显的变化.造成以上差异是由于本文模拟中泵波反射高度处电子温度为2000 K,比夜间对应高度处1000 K高得多,其电子能量更加容易损失.+20 s时(图 3c,图 3d),电子温度变化率变为30 %,也比LT20:00加热时的78.5%要小.此时电子密度的场向分布也没有夜间明显.随着加热持续,电子温度继续上升,在+120 s后(图 3e,图 3f),电子温度上升速度减小.电子浓度、电子温度均出现明显的场向结构,场向不均匀体纵向尺度更大,几乎整个模拟平面分为左右两部分,尤其是电子温度1578K等高线(1662 K下面一条,相邻等高线间温度之差均为84 K),高度从270 km一直延续到385 km,加热使得原本由电子温度谷隔开的两个电子温度峰连接在一起.仔细对比此时加热中心以及电子温度谷值处电子温度的变化可知,它们分别从1850 K、1306 K升高到2362 K、1909 K,谷值处电子温度的相对变化量反而更高.对比图 3e、3f,图 3g、3h可知,此时电子温度、电子浓度仍然没有稳定(更加详细的电子温度、电子浓度随时间变化的分析将在第3节给出).+600 s时(亦即加热机关机300 s)的电子浓度、电子温度空间剖面如图 3i、3j.此时电子温度有所降低,其最大相对变化率由+ 300 s(加热机关机时刻)时的52%变为28%,但没有如文献[11]模拟加热那样在加热结束后电子温度迅速下降到初始温度、电子浓度在加热结束后逐渐恢复到初始状态,其相对变化率反而由加热结束时的-7.5%降低为-10%.+900 s后,电离层电子温度比+600 s时进一步升高,而电子浓度则进一步降至-16%,另外电子温度最大变化率所在高度有所上升.
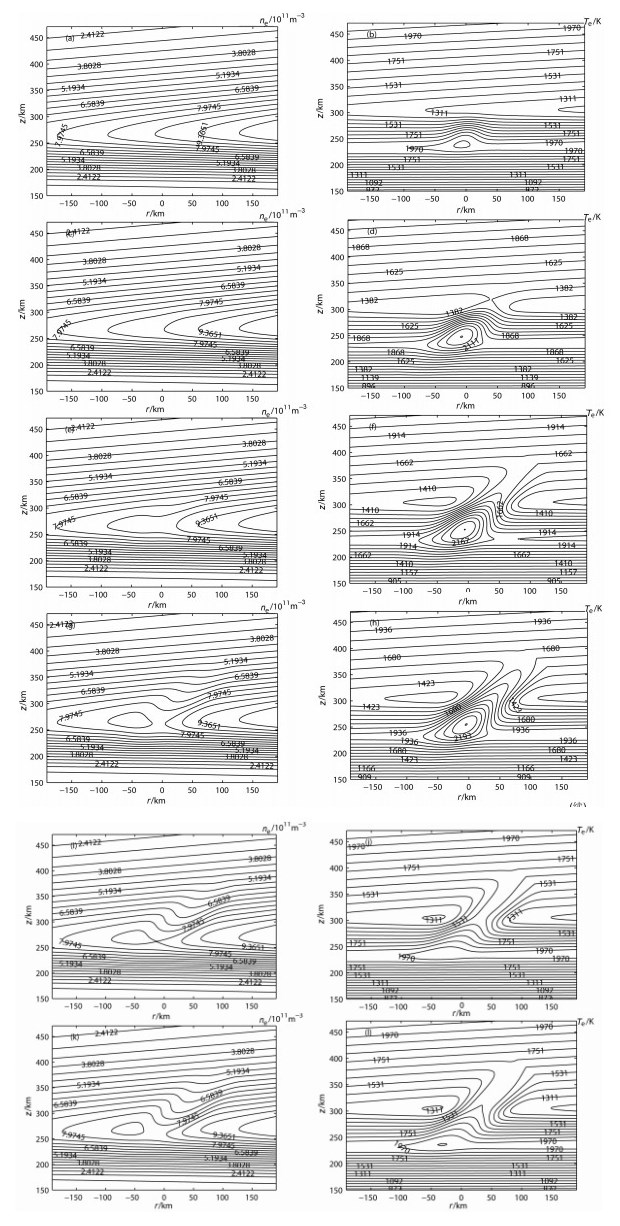
|
图 3 武汉地区下午16:00模拟加热不同时间后电子浓度、电子温度的二维空间剖面等高图 每图中相邻两条等高线之差相等,图中所标数值为该等高线代表的数值.(a)、(c)、(e)、(g)分别为加热2,20,120,300 s后电子浓度(1011m-3)等高图;(b)、(d)、(f)、(h)分别为加热2,20,120,300 s后电子温度(K)等高图;(i)(k)为关机300 s和600 s后电子浓度(1011m-3)等高图;(j)(l)为关机300 s和600 s后电子温度(K)等高图. Fig. 3 Contour maps of ne and Te at different time after the heating equipments turn on/off in the modeling heating (a)、(c)、(e)、(g) are contour map of ne 2, 20, 120, 300 s after turning on, respectively.(b)、(d)、(f)、(h) are contour map of Te 2, 20, 120, 300 s after turning on, respectively.(i) and (k) are contour map of ne 300 s and 600 s after turning off.(j) and (l) are contour map of Te after 300 s and 600 s after turning off |
在相同的物理模型和模拟方法下,使用基本相同的模拟条件,得到的模拟结果与文献[11]的结论差异明显.由于高频泵波加热电离层是一个非线性过程,涉及变化的参数众多,要找到导致上述结果的原因,完全通过公式解析推导非常困难.本文使用的方法是首先在模拟平面内选取部分有代表性的点,从模拟结果中导出部分参数值,结合加热模型,定量分析这些点上电子浓度、电子温度以及其他参数随时间的变化规律,并从中找出导致以上模拟结果的物理机制.
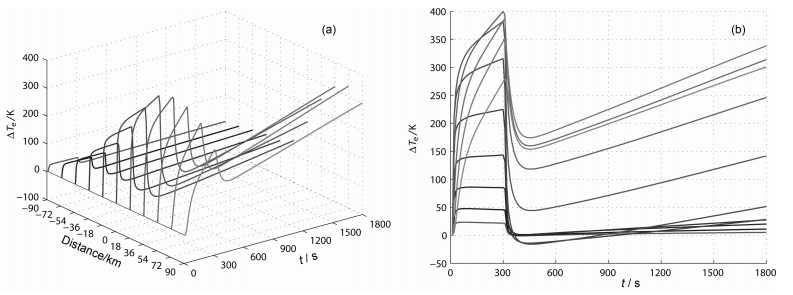
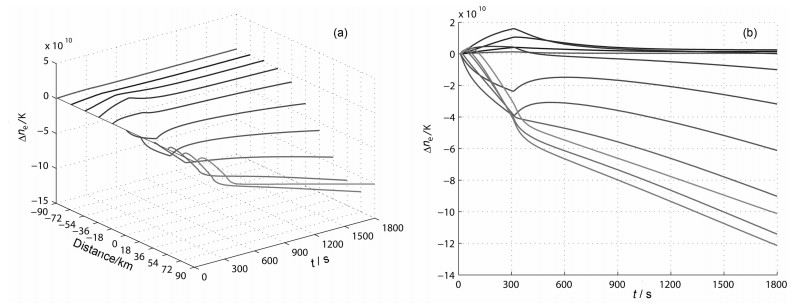
由于本文主要模拟区域为电离层F层,垂直于磁力线扩散系数相对很小,模型仅考虑了沿着磁力线方向上的扩散和热传导.为了更清晰地了解电子浓度、电子温度随时间变化,图 4,图 5分别给出经过加热中心所在磁力线上11个等间距点处(这11个点相对加热中心对称)电子温度和电子浓度相对加热前变化量随时间的变化(三维视图及侧视图).
|
图 4 选取的11个点处电子温度相对变化量随时间的变化 这些点位于同一条磁力线上,其中加热中心距离为0处是加热中心,点间距为18 km,负数表示沿磁力线方向往下的距离.(a)三视图;(b)侧视图. Fig. 4 The temporal dependence of absolute change of Te of the selected 11 points around the reflection height. The 11 points are in the same magnetic line.The dot pitch is 18 km.(a) Three-view drawing; (b) Profile plane. |
|
图 5 选取的11个点处电子浓度相对变化量随时间的变化 这些点位于同一条磁力线上,其中加热中心距离为0处是加热中心,点间距为18 km,负数表示沿磁力线方向往下的距离.(a)三视图;(b)侧视图. Fig. 5 The temporal dependence of absolute change of ne of the selected 11 points around the reflection height The 11 points are in the same magnetic line.The dot pitch is 18 km.(a) Three-view drawing; (b) Profile plane. |
从图 4中可明显看出:加热开始后,所选各点的电子温度相继出现不同幅度的上升,其中加热中心顺磁力线往下区域内(类似图 1中3区域,为了表述简便,下文简称3区域)各点电子温度响应时间最短,此处电子温度的饱和时间约为40s,而加热中心及其逆磁力线往上区域(下文简称2区域)各点处电子温度并没有饱和,还存在持续的小幅上升,且离加热中心越远的点随着泵波能量传导时间的增加,对加热机开机响应也越慢.而文献[11]模拟加热中,各点电子温度虽然饱和时间长短有别,但最长没有超过70 s.本文模拟加热结果的另一个重要特性就是加热结束后,图 1中三个区域,电子温度达到饱和,各点处电子温度迅速恢复到加热前状态,而2区域内几点处电子温度经过最长120 s的下降后(离加热中心越远,下降幅度以及下降速度越小)开始上升,其中最上面几点处的电子温度经过足够长时间的缓慢上升后甚至超过了加热结束前的电子温度,而文献[11]加热中所有点电子温度冷却时间均介于50~100 s间.
随着高频泵波对电离层的加热引起电子温度上升,导致等离子体膨胀,此时从图 4看出加热中心(及其上两点)处的电子浓度下降,其沿磁力线上下区域电子浓度均开始上升,出现上下两个电子浓度稠团,上稠团(图 1中区域2,下文类似)由于受到重力的作用在50~100 s内消失.另外加热中心顺磁力线往下点处电子浓度虽然有稳定的趋势,但是直到加热结束时,电子浓度仍没有稳定.
加热结束后,关于电子浓度的变化仍然可以分为加热中心上下两个区域,2区域电子浓度在+900 s时可以认为稳定,而其以上区域内电子浓度则继续下降,且下降速度不断缓慢变大,这一下降持续到加热结束后很长时间.值得注意的是此时加热中心附近两点(+18 km、0 km)处电子浓度在经过300 s的向初始状态回归(电子浓度上升),随后却便变为与3区域内几点处电子浓度同样的下降趋势.这与文献[11]中电子浓度在关机后都会向加热前大小回归,并在经过约600 s后稳定明显不同.
综合以上模拟结果,特别是图 4中+18 km、0 km两点处电子浓度在加热结束后先上升后下降的异常现象可知,电子温度在加热机关机后没有恢复到初始状态,并在之后开始缓慢上升,这是引起异常变化的主要原因.要解释以上异常现象,必须从电子能量方程入手.公式(5)、(6)分别给出加热开始前和加热结束后电子温度的平衡方程,这两个时刻泵波源项QHF皆为零:
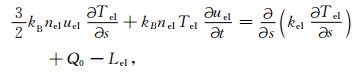
|
(5) |
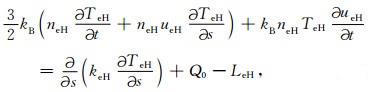
|
(6) |
其中的下标I,H分别表示加热开始前和加热结束后各项.
将(6)式减去(5)式,消去Q0后,得到加热结束后电子温度随时间变化率的方程,然后根据电离层电子温度、电子浓度等参数的空间剖面分布特点来分析模拟结果.为了使以后的计算尽量简便,考虑到电子能量公式(5)、(6)中的对流项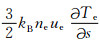
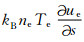
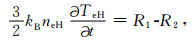
|
(7) |
其中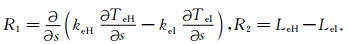
从上式可知,加热结束后电子温度变化由右边R1,R2决定,他们分别对应于热传导项和能量损失项相对加热前的变化.下面来详细地分析右边两项的大小.
由于模拟附近区域内的中性气体对热传导的影响很小,忽略其影响后热传导系数公式变为

|
(8) |
其中a为常数,可以看出ke,Te是正相关的.
对于第一项R1,电子温度的变化能同时影响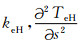
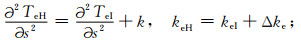
|
将以上几式带入(7),得到
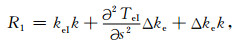
|
(9) |
(9)式右边各项分别表示电子温度二阶梯度变化、扩散系数变化、电子温度二阶梯度及扩散系数变化协同项(下文将分别用D,E,F表示),由于上式每个时刻的值依赖于初始以及当前时刻电子温度、电子浓度的分布,另外式中参数均为对磁场方向求梯度.下面直接利用从原有的对应时间的模拟加热结果中抽取出一条磁力线上的各种参量求不同时刻的R1以及其3分量D,E,F的大小,以解释模拟加热的异常现象.下文对公式(7)右边第二项R2的分析使用相同方法.
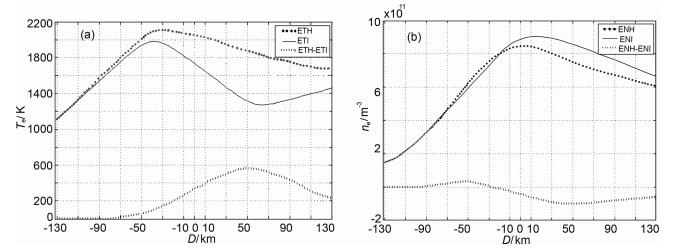
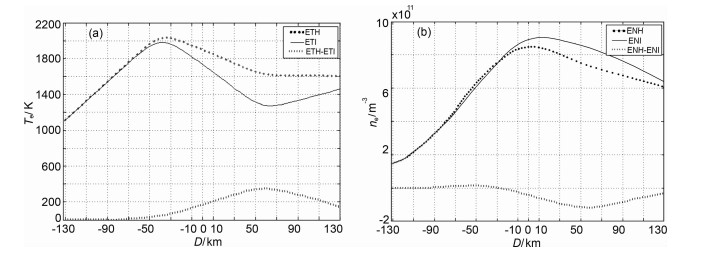
选取得到的等间隔点同样位于经过加热中心同一条磁力线上,且以加热中心为对称中心,点间距为2 km,共131个点.图 6、图 7分别给出这131点处+320 s、+600 s时电子浓度、电子温度,其从另一个侧面反应了模拟加热结果.从图中可知,电子温度上升最大并非位于加热中心处,而是初始电子温度谷值处,此处电子浓度相对下降率也最大.
|
图 6 +320 s时,经过加热中心磁力线上选取的131个点电子温度、电子浓度 点间距为2km,以加热中心为对称中心,ETI、EDI和ETH、EDH分别为初始和加热后的电子温度、电子浓度,虚线分别表示加热前后的变化量.(a)电子温度;(b)电子浓度. Fig. 6 The Te and ne of selected 131 points along the same magnetic line passing through there flect-height of the pump above the heating equipment at 320 seconds (20 seconds after turning off of heating) (a)Te of the selected points:(b)ne of the selected points |
|
图 7 +600 s时,经过加热中心磁力线上选取的131个点电子温度(a)、电子浓度(b) 点间距为2 km,以加热中心为对称中心,ETI、EDI和ETH、EDH分别为初始和加热后的电子温度、电子浓度,虚线分别表示加热前后的变化量.(a)电子温度;(b)电子浓度. Fig. 7 The Te and ne of selected 131 points along the same magnetic line passing through the reflect-height of the pump above the heating equipment at 600 seconds (300 seconds after turning off of heating) (a)Te of the selected points:(b)ne of the selected points. |
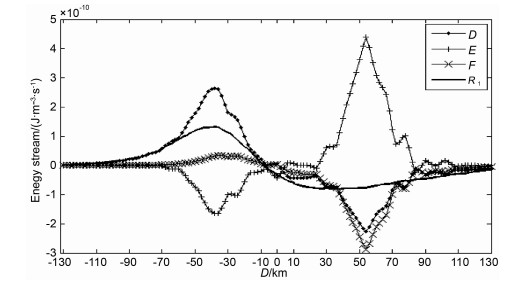
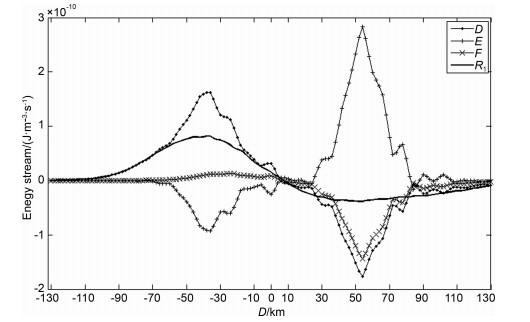
图 8和图 9分别是基于+320 s、+600 s时电子浓度电子温度计算得到的选取点上R1和D、E、F的大小.对比图 8、9可知,随着加热机关机时间增加,R1及其分量有所减少,这是由于此时电子温度开始向初始电子温度回归所致,可见直到此时,R1及其各分量仍然是在向初始状态趋近的;其次D,F在正负交界点从关机20 s时的-10 km移动到了+10 km附近,这进一步导致了R1最小值位置向右小幅移动.
|
图 8 +320 s后所取131点上R1,其3个分量D、E、F值 图中横坐标表示点到热中心距离,0 km处为加热中心. Fig. 8 Value of D, E, F and R1 at the selected 131 points at 320 seconds the x-coordinate is the distance between a points and the heating center The center of heating area around the reflect-height at the distance of 0 km. |
|
图 9 +600 s后选取131个点上R1、D、E、F的值 横轴说明同图 8. Fig. 9 Value of D, E, F and R1 at the selected 131 points at 600 seconds, the x-coordinate is the distance between a points and the heating center. The center of heating area around the reflect-height at the distance of 0 km. |
综合上述分析有以下结论:在+320 s、+600 s,图 4模拟加热中电子温度出现异常的-30 km到+90 km以上区域内,R1小于零,也就是该区域内电子温度上升引起了通过热传导损失的电子能量的增加.在模拟加热中,当电子温度被加热后R1将抑制电子温度的继续上升,在当加热结束后,其会进一步引起温度的下降,可见R1并不是导致电子温度异常的原因.
下面再来分析R2的变化,R2是加热前后由于电子与中性粒子,阳离子间复杂的相互作用引起的电子能量冷却率之差,其中Le由众多部分组成,数值模型中考虑了以下几种较重要的能量冷却机制:(1)电子-离子(包括电子与NO+,O2+,O+)弹性碰撞,(2)电子中性粒子(N2,O2,O,He)弹性碰撞,(3)中性分子的N2,O2旋转能级的激发,(4)N2,O2振动能级激发,(5)原子(O)电子能级激发,(6)原子(O)精细结构的激发等.但他们在高频泵波加热电离层中对电子温度的影响大小各不相同,经计算,其中1,4,6三项影响比其他项大得多,尤其在电离层较高高度处可以忽略其他因素的影响,这三项表达式分别如下[18]:
Le1电子与NO+,O2+,O+碰撞:
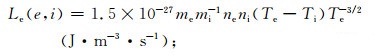
|
(10) |
Le4电子与中性分子N2,O2的碰撞:

|
(11a) |

|
(11b) |
其中:
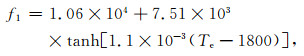
|
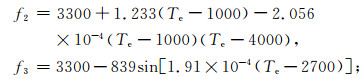
|
Le6:O原子精细结构激发:
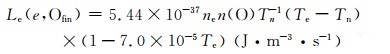
|
(12) |
设LE1=Le1H-Le1I,LE4=Le4H-Le4I,LE6=Le6H-Le6I,R2=LE1+LE4+LE6,下标I,H分别表示加热前后的值,图 10分别给出热机开机后不同时刻的131个点处LE1、LE4、LE6以及他们之和R2,以及对应时间计算得到的R1的值.
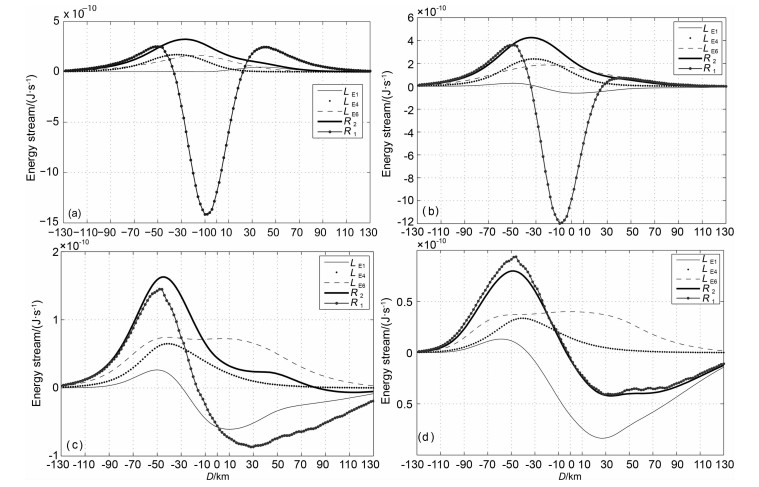
|
图 10 加热机开机不同时间后选取的131点处LE1,LE4,LE6以及它们之和R2的值 LE1、LE4、LE6、R2、R1值;(c)(d)关机20 s和300 s后选取131点处LE1、LE4、LE6、R2、R1值. Fig. 10 Value of LE1, LE4, LE6, R1 and R2 of the selected 131 points at four different time (a)20 s after turnon; (b)300 s after turnon; (c)20 s after turn off; (d)300 s after turn off. |
从图 10a可知,+20 s时,随着电子温度的强烈上升,电子与各中性粒子、阳离子等相互作用频率增加,电子能量冷却率增加,所以R2及其分量LE1,LE4,LE6均大于零.另外由公式(11a)、(11b)、(12)可知LE4,LE6与N2,O2,O浓度以及电子浓度成正比,中性粒子浓度随高度呈指数衰减,而电离层最大电子浓度在+10 km附近,LE4,LE6最大值必将在+10 km以下某处.这与图 10a结果一致.而LE1受到电子浓度与Te-Tn共同的影响,其最大值位于+40km处.此时3区域内电子温度基本饱和,随着加热的继续,2区域内电子温度将继续上升,Te-Tn的进一步增加使得LE6变大,直到在一段时间后LE6出现双驼峰.
从图 10b中可以看出,+300 s时,R1在+30km以上区域内基本上与R2相等,如果加热机此时不关机,加上泵波源项QHF,此时必然有
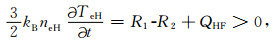
|
该区域内电子温度将继续上升,这就是为何图 4中电子温度直到关机前仍然在上升的原因.此时原来位于+40 km附近区域的LE1峰值消失了,取而代之的是加热中心附近区域的凹陷,亦即该区域内与电子和阳离子弹性碰撞有关的能量冷却反而随着电子温度上升后减小.对比此时加热中心附近区域R1,R2大小可知,R1-R2明显小于零,当加热机在此时关机后,该区域内电子温度迅速下降.
+320 s时,随着电子温度下降,LE4,LE6逐渐减小,LE1的作用开始凸现,R2在-10 km以上区域内已经明显受到LE1影响而减小,不过整体上R2在所有点上仍大于零.几乎选取的所有131个点处R1-R2均小于零,这与图 4电子温度在关机20 s后下降相一致.+600 s时LE1,LE4,LE6进一步减小,其中包括已经为负值的LE1,导致此时所有选取点上R1-R2>0,本还没有回复初始状态的电子温度开始上升.
下面结合加热中得到的各分量的值对下午加热中的异常现象进行解释.虽然本次模拟加热中泵波反射高度不高,但是由于此时电离层明显的电子温度双峰结构使得电子温度变化最大处位于320 km,随着高度的上升,N2,O2,O浓度呈指数衰减,与这三种浓度正相关的LE4、LE6开始变小,1区域内电子温度主要受到LE1的影响,其开始主导电子温度的变化.
由上文可知,3区域内电子温度的所有异常变化都是由于LE1没有随电子温度明显加热而上升甚至在某些区域内有所下降引起的.对比相同模拟条件下早上、下午、晚上不同时间模拟结果,引起下午LE1特殊变化的因素如下:首先从初始电子温度图 2中可以看出,所选取的下午电离层内电子温度的高度剖面呈双驼峰结构,上下驼峰处电子温度均为1970℃,对应高度分别为450 km和230 km,谷值处电子温度相对峰值处比早晚更低,约为峰值温度的2/3,高度约为300 km,更低的谷值电子温度导致其在加热后更强的上升,+300 s时其电子温度最大变化率为46%,而LT10:00[11]相应变化仅为22%.由图 6可知,虽然此时泵波反射点处电子温度仍为最高,但其绝对变化量反而比谷值处小.其次下午电离层反射区域内电子温度在加热前后都比文献[11]的更高,由图 11可知,温度越高,公式(10)中(Te-Ti)·Te-1.5项随温度的变化越小,在电子温度超过2500℃时,该项随电子温度的上升将保持不变甚至下降,LE1必然小于零.文献[19]就曾经提到过在高频加热中在电离层上F层内电子-离子的碰撞频率与电子温度之间存在复杂的依赖关系,当电子温度处于较高温度时,电子碰撞频率会随着电子温度的上升而下降.
由以上分析可知,下午特殊的电子温度空间结构才是模拟结果异常的根本原因,虽然并不是所有下午高频加热实验中都会出现类似不稳定性,但不可否认,此时电子浓度、电子温度特殊的空间结构更利于正反馈机制的形成.
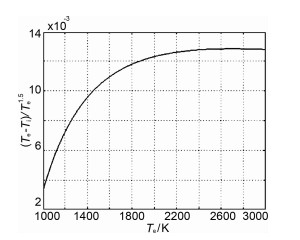
|
图 11 假设离子温度为1000 K时,项(Te-Ti)·Te-1.5随电子温度的关系 Fig. 11 The value of (Te-Ti)·Te-1.5 at different Te when Ti is 1000 K |
综合以上各模拟与分析结果可知,当电离层电子浓度、电子温度满足以下两个条件:第一,电离层电子温度随高度呈明显的双峰结构且电子温度谷值所在高度较高;第二,泵波的反射高度正好位于电子温度下峰值高度附近.一种正反馈机制形成,不稳定性被激发.此时电离层在高频泵波的加热下将会产生非常强烈的变化.通过对模拟结果的详细分析还可以得到以下结论:
(1)在加热泵波反射区域逆磁力线往上区域内,电子-离子的碰撞成为电子能量主要损失机制,当电子温度较高时,电子-离子碰撞引起的能量损失量基本不随电子温度的升高而升高,而是敏感的依赖于电子浓度的变化.
(2)由于已经处于加热机泵波照射区域以外,加热中心逆磁力线往上区域内电子温度、电子浓度受加热泵波的直接影响较小,而仅仅与电子热传导项和电子离子碰撞能量损失项有关,其中电子热传导项与电子温度的二阶梯度与热传导系数有关,与电子浓度变化无明显关联.
由于下午电离层背景电子浓度、电子温度都较高,且D、E层对泵波的吸收更强,电离层条件对高频加热电离层实验有一定负面影响,下午进行的加热实验较少,无法将其结果与本文模拟结果进行对比.但是文献[17]曾对在Arecibo进行的加热实验中加热中心逆磁力线往上区域内电子浓度、电子温度做过较详细的诊断观测,实验分析的结果与以上结论1、2基本相同.当电离层满足一定的条件时,在1、2结论的基础上正反馈机制引起的不稳定性是可以预期的,以上结论对今后的加热实验具有一定的指导作用,即在一些特殊的电离层状态下的电离层高频加热可能会得到非常强烈的加热效应.
为了简化模拟过程,本文没有考虑离子温度在加热过程中的变化,首先是因为其变化较小[16],另外从结论可知,离子温度的升高只会进一步的减弱电子-离子碰撞引起的电子能量损失.另外本文的模拟利用了文献[7]中对反射区域内电场估算方法,该方法没有考虑下午电离层D层,E层对泵波能量更加强的吸收,该吸收可能减小反射区域内的加热效应,这一因素将在以后的进一步研究中加以考虑.
| [1] | Burns C J, Hargreaves J K. The occurrence and properties of large-scale electron-density structures in the auroral F region. J. Atmos. Terr. Phys. , 1996, 58(1-4): 217-232. DOI:10.1016/0021-9169(95)00031-3 |
| [2] | Rodriguez P, Kennedy E J, Keskinen MJ, et al. The WIND-HA ARP experiment: Initial results of high power radiowave interactions with space plasmas. Geophys. Res. LeU. , 1998, 25: 257-260. DOI:10.1029/98GL00037 |
| [3] | Stubbe P. Review of ionospheric modification experiments at Tromsø. Auos. Terr. Phys. , 1996, 58: 349-368. DOI:10.1016/0021-9169(95)00041-0 |
| [4] | Ilagfors T, Kofman W, Kopka H, et al. Observations of enhanced plasma lines by EISCAT during heating experiments. Radio Sci. , 1983, 18(6): 861-866. DOI:10.1029/RS018i006p00861 |
| [5] | Showen R L, Duncan L M, Cragin B L. Observations of Plasma Instabilities in a Multiple Pump Ionospheric Heating Experiment. Geophys. Res. Lett. , 1978, 5(3): 187-190. DOI:10.1029/GL005i003p00187 |
| [6] | Gurevich A V. Nonlinear phenomena in the ionosphere. Springer-Verlag Press, 1978, New York |
| [7] | Bernhardt P A, Duncan L M. The feedback-diffraction theory of ionospheric heating. J. Aimos. Terr. Phys. , 1982, 44(12): 1061-1074. DOI:10.1016/0021-9169(82)90018-6 |
| [8] | Gorden W E, Carlson H C. Arecibo heating experiments. Radio SC. , 1974, 9: 1041-1047. DOI:10.1029/RS009i011p01041 |
| [9] | Gurevich A V. Effect of radio waves on the ionosphere in the vicinity of the F-layer. Geomagn. Aeron. , 1967, 7: 291-299. |
| [10] | Wong AY, et al. Observation of ionospheric cavitons. Phys, Rev.Lett. , 1987, 58: 1375-1379. DOI:10.1103/PhysRevLett.58.1375 |
| [11] | 邓峰, 赵正予, 张援农. 中低纬电离层加热大尺度场向不均勻体的二维数值模拟. 物理学报 , 2008, 58(10): 7382–7392. Deng F, Zhao Z Y, Zhang Y N, et al. Two-dimensional simulation of high-frequency-induced large-scale irregularities in F region. Aua Physica Sinica (in Chinese) , 2008, 58(10): 7382-7392. |
| [12] | Robinson T R. The heating of the high latitude ionosphere by high power radio waves. Physics Report , 1989, 179(2-3): 79-209. DOI:10.1016/0370-1573(89)90005-7 |
| [13] | Mantas G P, Carlson H C, Lahoz C H. Thermal response of the F region ionosphere in artificial modification experiments by HF radio waves. J.Geophys.Res. , 1981, 86(A2): 561-574. DOI:10.1029/JA086iA02p00561 |
| [14] | Newman A L, Carlson H C, Mantas G P, et al. Thermal response of the F-region ionosphere for conditions of large HF-induced electron-temperature enhancement. Geophys Res. Lett , 1988, 15: 311-314. DOI:10.1029/GL015i004p00311 |
| [15] | Djuth F T. Response of the Arecibo ionosphere to large HF-induced electron temperature enhancements. Advancss in Space Rsach , 1989, 9: 123-131. |
| [16] | IIansen J D, Morales G J, Duncan L M, et al. Large-scale HF-induced ionospheric modifications: Experiments. J.Geophys.Res. , 1992, 97(A1): 113-122. DOI:10.1029/91JA02403 |
| [17] | IIansen J D, Morales G J, Maggs J E. Large-scale HF-induced ionospheric modification: theory and modeling. J.Geophys. Res. , 1992, 97: 17019-17032. DOI:10.1029/92JA01603 |
| [18] | Schunk R W, Walker J C. Theoretical ion densities in the lower ionosphere. Space Phys. , 1980, 18: 813-820. DOI:10.1029/RG018i004p00813 |
| [19] | Robinson T R. The heating of the high latitude ionosphere by high power radio wave. Physics Report , 1989, 179(2/3): 79-209. |
| [20] | Meltz G, Iolway L H, Tomljanovich N M. Ionospheric heating by powerful radio waves. Radio Sci. , 1974, 9(11): 1049-1063. DOI:10.1029/RS009i011p01049 |
 2010, Vol. 53
2010, Vol. 53

